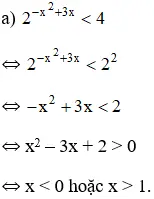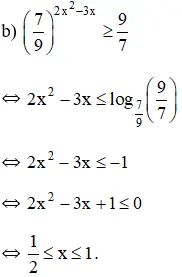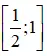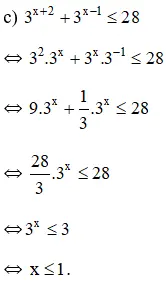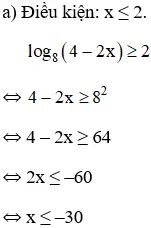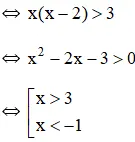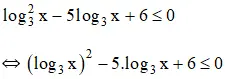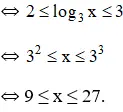Bất phương trình mũ và bất phương trình Logarit – Giải tích 12

5/5 - (4 bình chọn)

Series các bài giải hệ thống bài tập trong sách giáo khoa và sách bài tập Toán lớp 12, hỗ trợ các em tiết kiệm thời gian ôn luyện đạt hiệu quả nhất thông qua các phương pháp giải các dạng toán hay, nhanh và chính xác nhất. Dưới đây là lời giải bài tập SGK Bài 6: Bất phương trình mũ và bất phương trình lôgarit được đội ngũ chuyên gia của itoan giàu kinh nghiệm biên soạn và chia sẻ. Để giải các bài toán về bất phương trình mũ và bất phương trình lôgarit, các em học sinh cần nắm vững kiến thức lý thuyết và công thức tính quan trọng cùng sự linh hoạt trong việc sử dụng các công thức với các dạng toán khác nhau.CÙng học bài ngay thôi nào!

Mục tiêu bài học Bất phương trình mũ và bất phương trình Logarit

Sau bài học, chúng ta cần đạt được một số mục tiêu quan trọng như sau:

Nắm được cách giải các bất phương trình mũ, bất phương trình logarit dạng cơ bản, đơn giản.
Giải các dạng bài tập liên quan bất phương trình mũ, bất phương trình logarit.

Lý thuyết cần nắm bài Bất phương trình mũ và bất phương trình Logarit

Sau đây là những lý thuyết trọng tâm nhất được itoan biên soạn, giúp các bạn nắm vững bài học và tạo nền tảng giúp các bạn học sinh áp dụng giải các bài tập:

I. Bất phương trình mũ

1. Bất phương trình mũ cơ bản

a. Định nghĩa

Bất phương trình mũ cơ bản có dạng a^x>b (hoặc a^x≥b, a^x<b, a^x≤b) với a>0, a≠1

Ví dụ: 2^x≥3; 3^x<5 là các bất phương trình mũ

b. Cách giải

Ta xét bất phương trình dạng a^x>b .

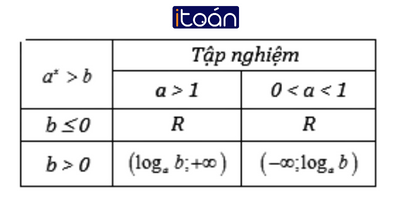
Nếu b≤0, tập nghiệm của bất phương trình là R vì a^x>0≥b, ∀x∈R.

Nếu b>0, bất phương trình tương đương với a^x>a^log_ab.

Với a>0 nghiệm của bất phương trình là x>log_ab.

Với 0<a<1, nghiệm của bất phương trình là x<log_ab.

Tập nghiệm của bất phương trình a^x>b được cho trong bảng sau:

Tương tự, ta có tập nghiệm của bất phương trình a^x<b được cho trong bảng sau:

2.Một số dạng bài bất phương trình mũ đơn giản.

a. Phương pháp đưa về cùng cơ số

Nếu a>1 thì a^f(x)<a^g(x)⇔f(x)<g(x)

Nếu 0<a<1 thì a^f(x)<a^g(x)⇔f(x)>g(x)

Ví dụ: Giải bất phương trình 3^x> 81

3^x>81 ⇔ 3^x>34

Vì cơ số 3 lớn hơn 1 nên x>4

Vậy tập nghiệm của bất phương trình đã cho là khoảng (4,+∞)

b. Phương pháp logarit hóa

Ví dụ: Giải bất phương trình 3^x+1>2^x

c. Phương pháp đặt ẩn phụ

Ví dụ: Giải bất phương trình 4^x−2.5^2x<10^x.

II. Bất phương trình logarit

1. Bất phương trình lôgarit cơ bản

a. Định nghĩa

Bất phương trình lôgarit cơ bản có dạng log_ax>b hoặc log_ax<b,log_ax≤b,log_ax≥b ,với a>0,a≠1.

Ví dụ: log₂x>6;log_0,5x>5 là các bất phương trình mũ lôgarit.

b. Cách giải

Xét bất phương trình log_ax>b

Trường hợp a>1 ta có: log_ax>b⇔x>a^b

Trường hợp 0<a<1 ta có: log_ax>b⇔0<x<a^b

2.Một số cách giải bất phương trình lôgarit đơn giản.

a. Biến đổi về cùng cơ số.

Nếu a>1 thì log_af(x)<log_ag(x)⇔0<f(x)<g(x).

Nếu 0<a<1 thì log_af(x)<log_ag(x)⇔0<g(x)<f(x).

b. Phương pháp mũ hóa

Ví dụ: Giải bất phương trình log₂(2^x+4)≥x+1

Giải

Vì 2^x+4>0,∀x∈R

Nên log₂(2^x+4)≥x+1⇔2^x+4≥2^x+1⇔2x≤4⇔x≤2

Vậy tập nghiệm của bất phương trình là (−∞;2].

c. Phương pháp đặt ẩn phụ

Ví dụ: Giải bất phương trình: (log₃x)²−5log₃x−6≤0

Bài học này khá nhiều lý thuyết quan trọng đúng không nào, các bạn có thể kết hợp học lý thuyết cùng video hướng dẫn dưới đây để nắm chắc kiến thức hơn nhé!

Hướng dẫn giải bài tập Bất phương trình mũ và bất phương trình Logarit

Phần bài tập trong sách giáo khoa rất sát với lý thuyết nên các bạn cố gắng hoàn thành hết nhé!

Trả lời câu hỏi Toán 12 Giải tích Bài 6 trang 86

Hãy lập bảng tương tự cho các bất phương trình a^x ≥ b, a^x < b, a^x ≤ b.

Hướng dẫn giải:

a^x > b	Tập nghiệm
a^x > b	a > 1	0 < a < 1
b ≤ 0	R	R
b > 0	[log_ab ; +∞)	(-∞,log_ab]

a^x < b	Tập nghiệm
a^x < b	a > 1	0 < a < 1
b ≤ 0	Vô nghiệm	Vô nghiệm
b > 0	(-∞,log_ab)	(log_ab ; +∞)

a^x ≤ b	Tập nghiệm
a^x ≤ b	a > 1	0 < a < 1
b ≤ 0	Vô nghiệm	Vô nghiệm
b > 0	(-∞,log_ab]	[log_ab ; +∞)

Đặt 2^x = t. ĐK: t > 0. Ta có phương trình đã cho tương đương với phương trình:

log_a⁡x ≥ b	a > 1	0 < a < 1
Nghiệm	x ≥ a^b	0 < x ≤ a^b

log_ax < b	a > 1	0 < a < 1
Nghiệm	0 < x < a^b	x > a^b

log_a⁡x ≤ b	a > 1	0 < a < 1
Nghiệm	0 < x ≤ a^b	x ≥ a^b

(1) ⇔ 3x + 1 < 2x + 3 ⇔ x < -2.

Bài 1 (trang 89 SGK Giải tích 12): Tính

Hướng dẫn giải:

Vậy phương trình có tập nghiệm S = (-∞; 0) ∪ (1; +∞)

Vậy bất phương trình có tập nghiệm

Vậy bất phương trình có tập nghiệm (-∞; 1]

Vậy bất phương trình có tập nghiệm S = (-∞; 0) ∪ (1; +∞)

Bài 2 (trang 90 SGK Giải tích 12): Giải các bất phương trình:

Lời giải:

Vậy bất phương trình có tập nghiệm (-∞; -30)

Kết hợp với điều kiện xác định được x > 3.

Vậy bất phương trình có tập nghiệm (3; +∞).

d) Điều kiện: x > 0.

(Bất phương trình bậc hai ẩn log₃x).

Vậy bất phương trình có tập nghiệm [9; 27].

Lời kết sau bài học Bất phương trình mũ và bất phương trình Logarit

Bài học Bất phương trình mũ và bất phương trình logarit không khó đúng không các bạn? Các bạn đã nắm hết chưa nhỉ? Hy vọng với bài giảng chi tiết, dễ hiểu trên, các bạn đã nắm vững được kiến thức và áp dụng được linh hoạt trong tình huống thực tế. Ngoài ra, các bạn có thể truy cập vào trang web Toppy. Với đội ngũ giảng viên tâm huyết, nhiệt tình, Toppy luôn sẵn sàng giúp đỡ khi con gặp bất kì khó khăn nào trong học tập. Chúc các bạn luôn học tập tốt!

Xem thêm một số bài giảng liên quan khác tại đây:

Bất phương trình mũ và bất phương trình Logarit – Giải tích 12

Mục tiêu bài học Bất phương trình mũ và bất phương trình Logarit