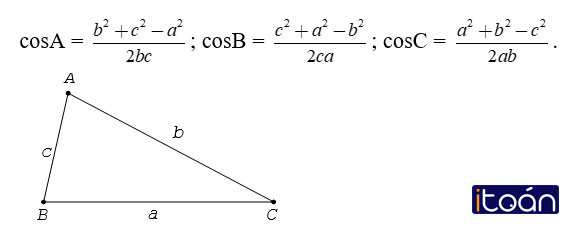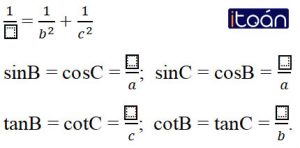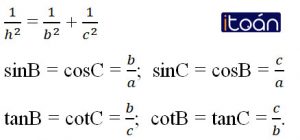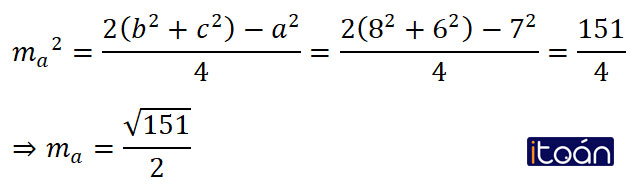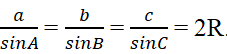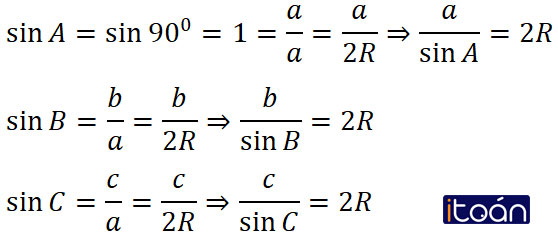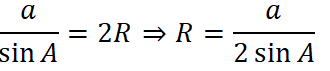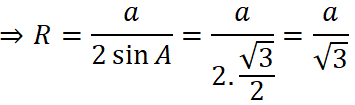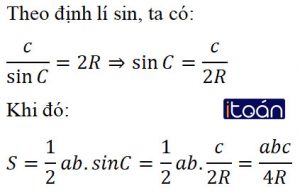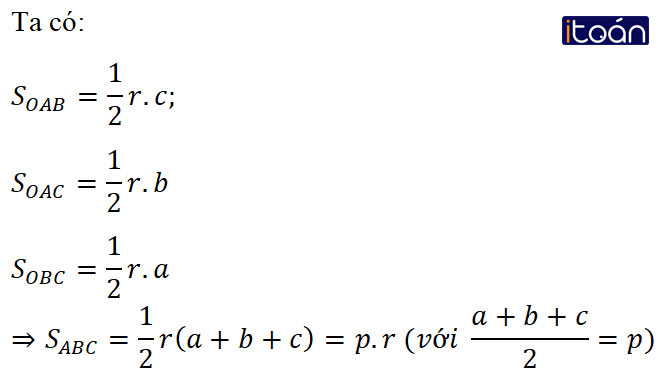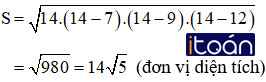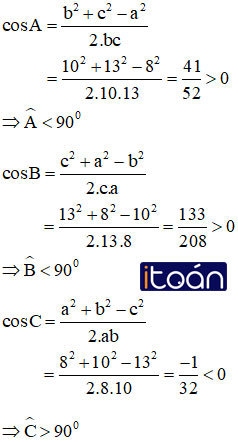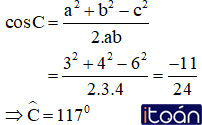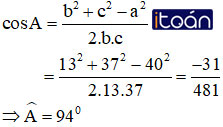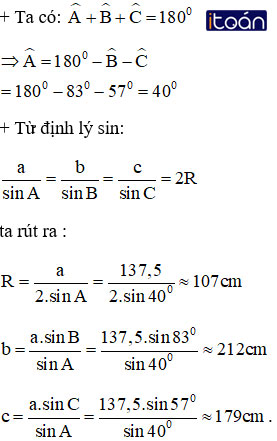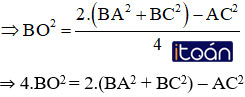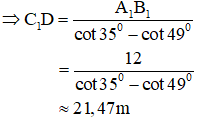Các hệ thức lượng trọng tam giác và giải tam giác – Hình học 10

Xin chào các bạn học sinh thân mến! Hôm nay, chúng ta cùng tiếp tục học bài Các hệ thức lượng trọng tam giác và giải tam giác. Vậy Các hệ thức lượng trọng tam giác và giải tam giác là gì? Đây là một trong những kiến thức quan trọng của chương trình hình học lớp 10. Do đó, các em hãy ghi chú bài vở và nắm kiến thức bài hôm nay thật cẩn thận nhé. Sau đây, itoan sẽ cùng các em tìm hiểu bài Các hệ thức lượng trọng tam giác và giải tam giác. Cùng itoan theo dõi nha!
Mục tiêu bài học
Trước khi đi vào bài học chính, các em hãy cùng iToan xác định mục tiêu cần đạt được sau buổi học ngày hôm nay nhé!
- Nắm chắc lý thuyết: Các hệ thức lượng trọng tam giác và giải tam giác là gì và cách làm như thế nào?
- Nắm chắc và hiểu cách làm bài tập.
- Sau khi học xong bài học này, các bạn học sinh sẽ nắm được kiến thức Các hệ thức lượng trọng tam giác và giải tam giác cũng như phương pháp xử lý từng dạng bài tập.
Kiến thức cần
1. Định lí côsin
Cho tam giác ABC có BC = a, AC = b và AB = c
Ta có
- a2 = b2 + c2 – 2bc.cosA;
- b2 = c2 + a2 – 2ca.cosB;
- c2 = a2 + b2 – 2ab.cosC.
Hệ quả
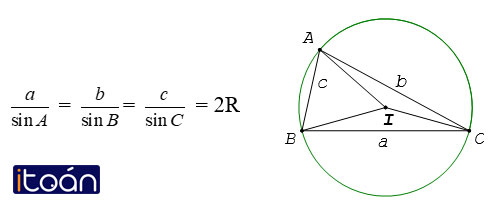
2. Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Ta có
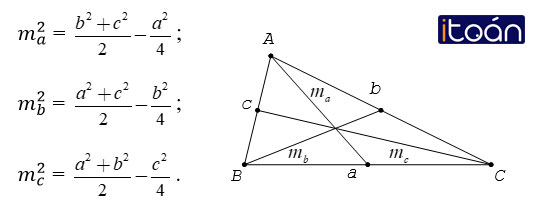
3. Độ dài đường trung tuyến
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
Ta có
4. Công thức tính diện tích tam giác
Cho tam giác ABC có
- ha, hb, hc là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB;
- R là bán kính đường tròn ngoại tiếp tam giác;
- r là bán kính đường tròn nội tiếp tam giác;
- p = (a + b + c)/2
- S là diện tích tam giác.
Khi đó ta có:
Giải bài tập các hệ thức lượng trọng tam giác và giải tam giác trong sách giáo khoa
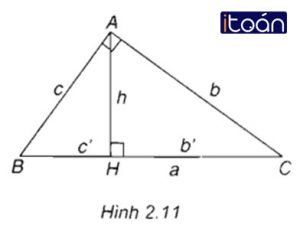
Bài 3 trang 46 sgk
a2 = b2 + (…..)
b2 = a x (…..)
c2 = a x (…..)
h2 = b’ x (…..)
ah = b x (…..)
Hướng dẫn giải:
a2 = b2 + c2
b2 = a x b’
c2 = a x c’
h2 = b’ x c’
ah = b x c
Bài 3 trang 48
Khi ABC là tam giác vuông, định lý côsin trở thành định lý quen thuộc nào ?
Hướng dẫn giải:
Khi ABC là tam giác vuông, định lý côsin trở thành định lý Py- ta – go.
Bài 3 trang 49
Cho tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến ma của tam giác ABC đã cho.
Bài 3 trang 50
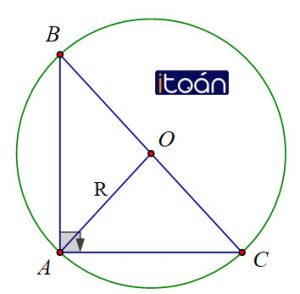
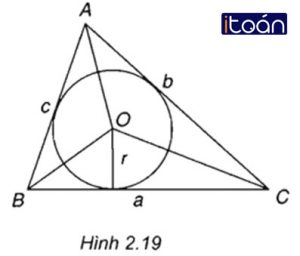
Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.
Chứng minh hệ thức:
Hướng dẫn giải:
Do tam giác ABC vuông tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC ⇒ BC = a = 2R.
Ta có:
Bài 3 trang 52
Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó. Theo định lí sin ta có:
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
Bài 3 trang 53
Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.
Hướng dẫn giải:
S = 1/2 a.ha = 1/2 b.hb = 1/2 c.hc
Bài 3 trang 54
Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.
Hướng dẫn giải:
Bài 1 trang 59 SGK Hình học 10
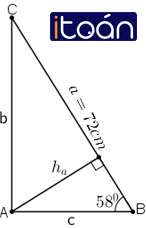
Cho tam giác ABC vuông tại A, B̂ = 58o và cạnh a = 72cm. Tính Ĉ, cạnh b và đường cao ha.
Hướng dẫn giải:
- Ĉ + B̂ = 90º ⇒ Ĉ = 90º – B̂ = 90º – 58º = 32º
- b = a.sinB = 72 . sin 58º ≈ 61,06 cm
- c = a . cos B = 72 . cos 58º ≈ 38,15cm
- ha = c . sin B = 38,15 . sin 58º = 32,36 cm.
Bài 2 (trang 59 SGK Hình học 10)
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
Hướng dẫn giải:
Bài 3 (trang 59 SGK Hình học 10):
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
Hướng dẫn giải:
a2 = b2 + c2 – 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129 ⇒ a = √129 cm
Bài 4 (trang 59 SGK Hình học 10):
Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
Nửa chu vi của tam giác: p = (7 + 9 + 12)/2 = 14. Áp dụng công thức Hê–rông ta có:
Bài 5 (trang 59 SGK Hình học 10):
Cho tam giác ABC có Â = 120o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A = m2 + n2 – 2.m.n.cos120º = m2 + n2 + mn
⇒ BC = √( m2 + n2 + mn).
Bài 6 (trang 59 SGK Hình học 10):
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Hướng dẫn giải:
a) Ta có:
Vậy tam giác ABC có góc C tù.
Bài 7 (trang 59 SGK Hình học 10):
Tính góc lớn nhất của tam giác ABC biết:
a) Các cạnh a = 3cm, b = 4cm và c = 6cm;
b) Các cạnh a = 40cm, b = 13cm, c = 37cm.
Hướng dẫn giải:
Nhận xét:
Trong một tam giác, góc đối diện với cạnh lớn nhất là góc lớn nhất.
a) Cạnh c = 6cm lớn nhất nên góc lớn nhất là góc C:
Vậy góc lớn nhất là 117º.
b) Cạnh a = 40cm lớn nhất suy ra góc lớn nhất là góc A:
Vậy góc lớn nhất bằng 94º
Bài 8 (trang 59 SGK Hình học 10):
Cho tam giác ABC biết cạnh a = 137,5cm, ∠B = 83o và ∠C = 57o. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
Hướng dẫn giải:
Bài 9 (trang 59 SGK Hình học 10):
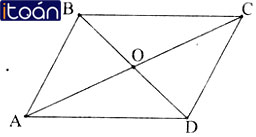
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
Hướng dẫn giải:
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD. Xét ΔABC có BO là trung tuyến:
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2 ⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Bài 10 (trang 60 SGK Hình học 10):
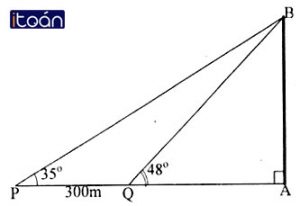
Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc ∠BPA = 35o và ∠BQA = 48o. Tính chiều cao của tháp.
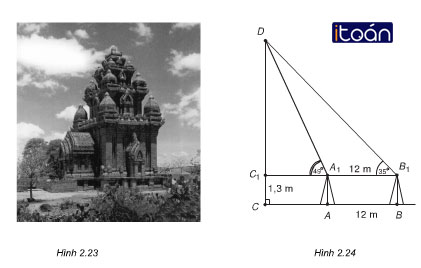
Bài 11 (trang 60 SGK Hình học 10):
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được ∠DA1C1 = 49o và ∠DB1C1 = 35o. Tính chiều cao CD của tháp đó.
Ta có: A1B1 = AB = 12 m.
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 – C1A1 = C1D.cot35o – C1D.cot49o = C1D.(cot35o – cot49o) = C1D.(cot35o – cot49o)
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.
Lời kết
Bài học về Các hệ thức lượng trọng tam giác và giải tam giác kết thúc tại đây. iToan hi vọng các em đã có những phút giây học vừa hiệu quả vừa thư giãn cùng với các thầy cô. Nếu các em còn thắc mắc vấn đề gì hãy liên hệ với iToan để được giải đáp và tư vấn nhé! Hẹn các em trong buổi học khác.
Xem thêm: