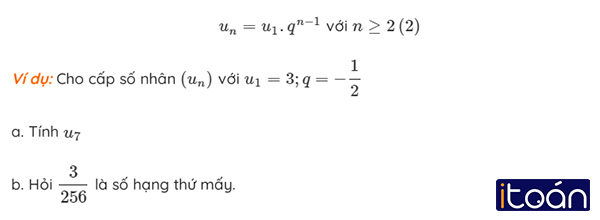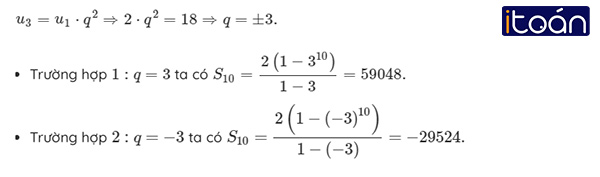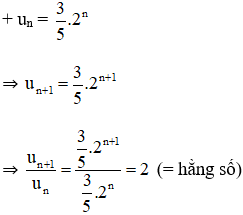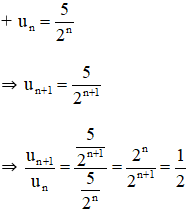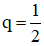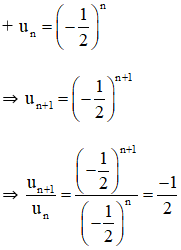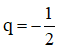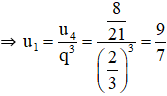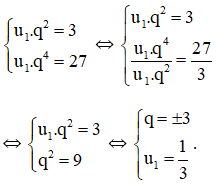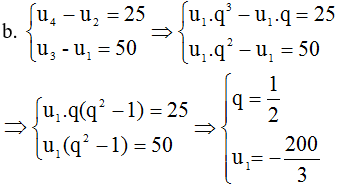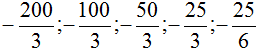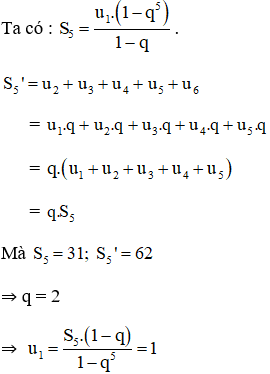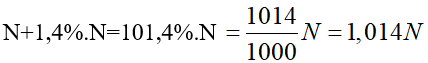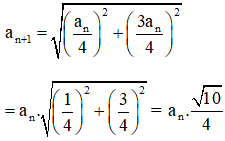Cấp số nhân – Bài tập &Lời giải Đại số 11

Tiếp theo bài Cấp số cộng hôm trước, hôm nay chúng ta sẽ cùng tìm hiểu về Cấp số nhân. Bài giảng được iToan biên soạn, với mục đích tổng hợp lại các kiến thức cần nắm, hướng dẫn giải bài tập SGK Đại số 11 và giúp các em nâng cao kiến thức qua những bài tập tự luyện.
Lý thuyết cần nắm về Cấp số nhân
Sau đây là tổng hợp lý thuyết ngắn gọn & dễ hiểu nhất, giúp các em nắm được kiến thức và kĩ năng cần thiết!
Định nghĩa
Định nghĩa
- Cấp số nhân là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó và một số không đổi q.
- Số q được gọi là công bội của cấp số nhân.
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi un+1=un.q với n∈N∗(1)
- Đặc biệt:
– Khi q=0, cấp số nhân có dạng u1,0,0,...,0,...
– Khi q=1, cấp số nhân có dạng u1,u1,u1,...,u1,...
– Khi u1=0 thì với mọi q, cấp số nhân có dạng 0,0,0,...,0,...
Ví dụ: Chứng minh dãy số sau là cấp số nhân: −4,1,−1/4,1/16,−1/64.
Giải
Vì:
1=(−4).(−1/4);−1/4=1.(−1/4);
1/16=(−1/4).(−1/4);−1/64=1/16.(−1/4);
Nên dãy số −4,1,−1/4,1/16,−1/64 là một cấp số nhân với công bội q=−1/4
Số hạng tổng quát
Định lý 1: Nếu cấp số nhân có số hạng đầu u1 và công bội q≠0 thì số hạng tổng quát un của nó được tính bởi công thức:
Giải
a. Áp dụng công thức (2) ta có:
u7=u1.q^6=3.(−1/2)^6=3/64.
b. Theo công thức (2) ta có:
un=3⋅(−1/2)^n−1=3/256⇔(−1/2)^n−1=1/256=(−1/2)^8.
⇔n−1=8⇔n=9
Vậy số 3/256 là số hạng thứ chín.
Tính chất các số hạng của cấp số nhân
Định lý 2: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, tức là:
Hệ quả: Nếu a,b,c là ba số khác 0, thì ba số a,b,c (theo thứ tự đó) lập thành một cấp số nhân khi và chỉ khi b^2=ac.
Tổng n số hạng đầu của một cấp số nhân
Chú ý: Nếu q=1 thì Sn=n.u1.
Ví dụ: Cho cấp số nhân (un), biết u1=2;u3=18. Tính tổng của mười số hạng đầu tiên.
Giải
Theo giả thiết u1=2;u3=18. Ta có:
Giải bài tập SGK Đại sô 11 Cấp số nhân
Bài 1 (trang 103 SGK Đại số 11):
Chứng minh các dãy số 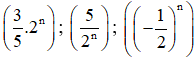
Lời giải:
⇒ (un) là cấp số nhân với công bội q = 2.
⇒ (un) là cấp số nhân với công bội
⇒ (un) là cấp số nhân với công bội
Bài 2 (trang 103 SGK Đại số 11):
Cho cấp số nhân (un) với công bội q
a.Biết u1 = 2, u6 = 486. Tìm q
b.Biết q = 2/3 , u4 = 8/21 . Tìm u1
c.Biết u1 = 3, q = -2. Hỏi số 192 là số hạng thứ mấy?
Lời giải:
a. Ta có: u6 = u1.q5
hay 486 = 2.q5
⇒ q5 = 243
⇒ q = 3.
b. u4 = u1.q3
c. un = u1.qn – 1
hay 192 = 3.(-2)n – 1
⇒ (-2)n – 1 = 64
⇒ (-2)n – 1 = (-2)6
⇒ n – 1 = 6
⇒ n = 7.
Vậy u7 = 192.
Bài 3 (trang 103 SGK Đại số 11):
Tìm các số hạng của cấp số nhân (un) có năm số hạng, biết:
a.u3 = 3 và u5 = 27
b.u4 – u2 = 25 và u3 – u1 = 50
Lời giải:
Giả sử CSN (un) có công bội q.
a. Ta có: u3 = u1.q2 ; u5 = u1.q5.
Theo đề bài, ta có hệ phương trình :
+ Với q = 3 ta có cấp số nhân : 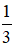
+ Với q = -3 ta có cấp số nhân : 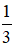
Vậy 5 số hạng là:
Bài 4 (trang 104 SGK Đại số 11):
Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.
Lời giải:
Gọi cấp số nhân (un) cần tìm có công bội q, số hạng đầu tiên u1.
Vậy CSN (un) là: 1; 2; 4; 8; 16; 32
Bài 5 (trang 104 SGK Đại số 11):
Tỷ lệ tăng dân số của tỉnh x là 1,4%. Biết rằng dân số của tỉnh hiện nay là 1, 8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm thì dân số của tỉnh đó tăng bao nhiêu?
Lời giải:
Giả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N
Vậy số dân của tỉnh đó vào năm sau là
Theo tỷ lệ tăng dân số 1,4% thì dân số hàng năm của tỉnh x là các số hạng của cấp số nhân với công bội q = 1,014
Và số hạng đầu u1 = 1,8 triệu
Theo công thức: un = u1.qn – 1
⇒ Dân số của tỉnh x sau 5 năm sau là:
u6 = 1,8.(1,014)5 ≈ 1.93 triệu (người)
⇒ Dân số sau 10 năm là:
u11 = 1,8.(1,014)10 ≈ 2.07 triệu (người).
Bài 6 (trang 104 SGK Đại số 11):
Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C1 (hình bên). Từ hình vuông C2 lại tiếp tục như trên để được hình vuông C3… Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C1, C2, C3, …,Cn
Gọi an là độ dài cạnh của hình vuông Cn. Chứng minh dãy số (an) là một cấp số nhân.
Lời giải:
Cạnh của hình vuông C1 là: a1 = 4 (giả thiết)
Giả sử cạnh hình vuông thứ n là an.
Theo định lý Py-ta-go : Cạnh hình vuông thứ n + 1 là :
Bài tập tự luyện Cấp số nhân
Các em hãy làm thêm nhiều bài tập tự luyện để củng cố và ghi nhớ kiến thức tốt hơn!
Phần câu hỏi
Câu 1: Cho dãy số: –1; 1; –1; 1; –1; … Khẳng định nào sau đây là đúng?
A. Dãy số này không phải là cấp số nhân
B. Số hạng tổng quát un = 1n =1
C. Dãy số này là cấp số nhân có u1= –1, q = –1
D. Số hạng tổng quát un = (–1)^2n.
Câu 2: Cho dãy số : 1/2; 1/4; 1/8; 1/16; ... . Khẳng định nào sau đây là sai?
A. Dãy số này là cấp số nhân có u1=1,q=1/2
B. Số hạng tổng quát un=1/ 2^(n−1)
C. Số hạng tổng quát un=1/ 2^n
D. Dãy số này là dãy số giảm
Câu 3: Cho dãy số: –1; –1; –1; –1; –1; … Khẳng định nào sau đây là đúng?
A. Dãy số này không phải là cấp số nhân.
B. Là cấp số nhân có u1=−1; q = 1
C. Số hạng tổng quát un=1/ 2^n
D. Dãy số này là dãy số giảm
Câu 4: Cho cấp số nhân un với u1=−2; q = – 5 . Viết 3 số hạng tiếp theo và số hạng tổng quát un ?
Câu 5: Cho cấp số nhân un với u1=3; q = −2. Số 192 là số hạng thứ mấy của un ?
A. Số hạng thứ 5.
B. Số hạng thứ 6.
C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho.
Phần đáp án
1.C 2.B 3.B 4.D 5.C
Lời kết
Bài giảng Cấp số nhân kết thúc tại đây. Hẹn lại các em tại bài học thú vị tiếp theo. Để học tốt môn toán 11 cũng như các môn học khác, các em có thể học trực tuyến với Toppy. Toppy có đầy đủ hệ thống bài giảng theo từng chủ đề, và bài tập từ cơ bản đến nâng cao, giúp các em tiến bộ qua từng bài học.
Chúc các em luôn học tốt!
>>Xem thêm:
- Tính chất chia hết của một tổng
- Tập hợp Q các số hữu tỉ
- Ước và bội
- Nguyên hàm- Giải tích 12
- Tích phân- Giải tích 12