Lý thuyết & Bài tập: Diện tích hình hộp chữ nhật – Hình học Toán 8

Hình hộp chữ nhật là kiến thức cơ bản của hình học Toán 8. Hình hộp chữ nhật xuất hiện rất nhiều trong cuộc sống. Cách tính diện tích, thể tích, các đặc điểm, tính chất của hình học này sẽ được Itoan giải đáp trong bài viết sau. Hãy khám phá ngay thôi nào:
Khái niệm về hình hộp chữ nhật
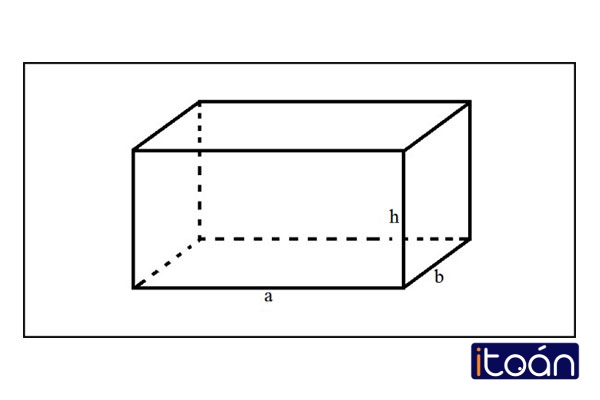
- Hình hộp chữ nhật (có tên tiếng Anh là Rectangular Prism) là một loại hình trong hình học không gian. Nó gồm có:
Sáu mặt đều là hình chữ nhật - Tám đỉnh và mười hai cạnh.
Lấy hai mặt đối diện nhau gọi là hai mặt đáy. Bốn mặt còn lại xung quanh gọi là các mặt bên.
Cũng như các loại hình học khác, khối hình hộp này cũng có các tính chất riêng để có thể nhận biết:
- Cấu trúc của một hình hộp chữ nhật gồm: 12 cạnh, 8 đỉnh và 6 mặt diện tích hình chữ nhật.
- Các đường chéo lấy hai đầu mút là hai đỉnh thuộc hai mặt phẳng đối nhau thì sẽ đồng quy tại một điểm.
- Diện tích của các hình chữ nhật đối diện nhau là bằng nhau.
- Chu vi của hai mặt đối diện nhau cũng bằng nhau.
Công thức tính chu vi hình hộp chữ nhật
Chu vi được hiểu là đường bao quanh một hình phẳng. Cánh tính chu vi hình hộp chữ nhật là cộng tổng tất cả 12 cạnh bên và cả cạnh đáy. Tức là tổng chiều cao, chiều dài, chiều rộng của hình hộp và nhân cho 4 lần.
Công thức : C = 4 × (h+a +b)
Chú thích cho công thức trên:
- C là kí hiệu chung của chu vi của một hình bất kỳ.
- h là chiều cao của khối hình hộp đó.
- a, b lần lượt là chiều dài và chiều rộng của mặt đáy hình hộp.
Công thức tính các loại diện tích hình hộp chữ nhật
Diện tích xung quanh
Diện tích xung quanh là phần 4 diện tích hình chữ nhật được coi là các mặt bên của khối hình hộp.
Vì các mặt đối diện nhau sẽ có phần diện tích bằng nhau. Nên có thể tính diện tích xung quanh bằng cách tính chu vi đáy của khối hình hộp và nhân với chiều cao của nó.
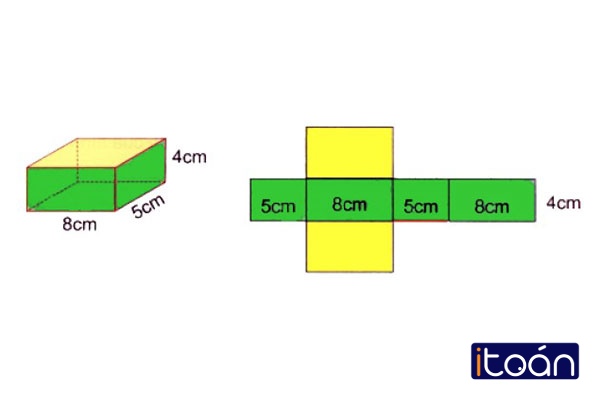
Công thức : Sxq = 2h × (a + b)
Chú thích cho công thức trên:
- Sxq là kí hiệu cho phần diện tích xung quanh của hình hộp
- h, a, b lần lượt là chiều cao, chiều dài và chiều rộng của khối hình hộp
Diện tích toàn phần
Cũng như vậy với phần diện tích toàn phần, đây là phần diện tích hình hộp chữ nhật bao quanh nó. Bao gồm tổng tất cả 6 mặt chữ nhật cộng lại sẽ ra được phần diện tích toàn phần.
Để có thể tính được diện tích toàn phần, ta sẽ cộng phần diện tích xung quanh đã tính ở trên và thêm với phần diện tích hai mặt đáy.
Công thức: Stp = Sxq + 2× Sđáy
Chú thích cho công thức trên:
- Stp là kí hiệu cho phần diện tích toàn phần của hình hộp
- Sxq là kí hiệu cho phần diện tích toàn phần của hình hộp
- Sđáy là kí hiệu của diện tích mặt đáy của hình hộp
Công thức tính thể tích hình hộp chữ nhật
Thể tích hay dung tích được hiểu là lượng không gian mà vật đó chiếm. Thể tích của hình hộp chữ nhật được xác định khi đã có đủ dữ liệu về:
- Chiều dài
- Chiều rộng
- Đường cao
Để có thể tính được thể tích ta chỉ cần tính được diện tích một mặt chữ nhật và nhân chiều cao tương ứng của mặt đó.
Công thức: V= a × b×h
Chú thích cho công thức trên:
- V là ký hiệu tính thể tích hình chữ nhật khối hộp
- a, b, h lần lượt là các đại lượng chỉ chiều dài, chiều rộng và chiều cao tương ứng của khối hình.
Đường chéo
Một trong những đại lượng quan trọng trong hình không gian chính là đường chéo. Công thức tính của đường chéo như sau: D= √(a2 + b2+h2)
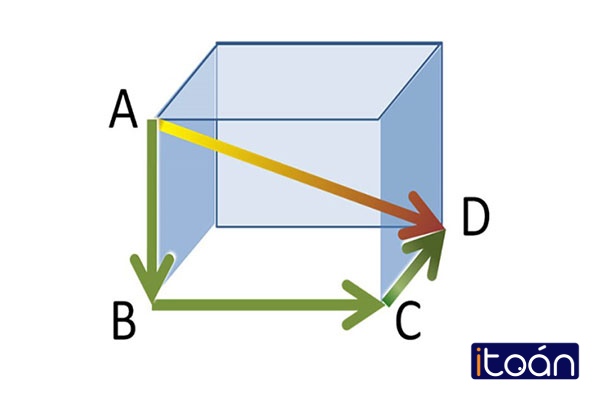
Chú thích cho công thức trên:
- D là kí hiệu của đường chéo
- a, b, h lần lượt là các đại lượng chỉ chiều dài, chiều rộng và chiều cao tương ứng của khối hình.
Với các công thức trên, các bạn có thể áp dụng trong cuộc sống rất nhiều. Từ xây dựng, các công việc thủ công hay cũng có thể giúp cho các bạn học sinh hoàn thành bài tập của mình. Hy vọng với bài viết trên thì Itoan đã cung cấp cho các bạn công thức diện tích hình hộp chữ nhật, thể tích và cả đường chéo của nó. Chúc các bạn thành công!
>> Xem thêm: Các trường hợp đồng dạng của tam giác vuông – Học tốt toán 8
