Đồ thị hàm số y = ax + b – Học tốt toán lớp 7 cùng iToan

Đồ thị hàm số y = ax + b là gì? là một trong những kiến thức quan trọng xuyên suốt chương trình học toán của các em. Do đó, các em cần phải nắm chắc và hiểu rõ bài học ngày hôm nay. Kiến thức trong buổi học hôm nay sẽ làm nền tảng để các em học tốt môn toán khi càng lên cao. Vậy đồ thị hàm số y = ax + b là gì và cách ứng dụng vào bài tập ra sao. Cùng iToan tìm hiểu nhé.

Mục tiêu bài học đồ thị hàm số y = ax + b

Trước khi đến với bài học ngày hôm nay, itoan sẽ cùng các em đặt ra mục tiêu và cố gắng đạt được nó nhé!

• Hiểu thế nào là đồ thị hàm số y = ax+b
• Vận dụng định lý vào bài tập

Lý thuyết bài học đồ thị hàm số y = ax + b

Đồ thị hàm số y = ax + b là gì?

Lý thuyết

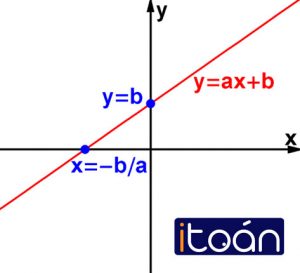
Đồ thị hàm số y=ax + b (với a b là tham số a khác 0) cắt trục tung tại điểm có tung độ bằng b.

Bên cạnh đó, đồ thị hàm số y = ax + b song song với trục 0x nếu b = 0 và song song với đường thẳng y = ax nếu b ≠ 0.

Đồ thị này cũng được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

Chú ý: Đồ thị hàm số y = ax + b cắt trục hoành tại điểm Q(-b/a; 0) với a ≠ 0.

Bài tập ví dụ

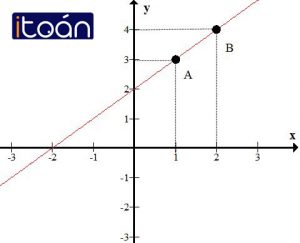
Ví dụ : vẽ đồ thị của hàm số  y = x + 2

Hướng dẫn giải:

TXD: D=R

Ta có :a=1>0: hàm số đồng biến.

Bảng giá trị :

Đồ thị của hàm số  y = x+2 là đường thẳng đi qua hai điểm A(1;3) và B(2;4).

Luyện tập vẽ Đồ thị hàm số y = ax + b

• Bước 1: chọn điểm B(0;b) trên trục Oy
• Bước 2: chọn điểm A(-b/a;0) trên trục Ox
• Bước 3: kẻ đường thẳng AB

Phương pháp tìm tọa độ giao điểm của hai đường thẳng

• Bước 1: Gọi A(x₀; y₀) là giao điểm của (d₁): y = f₁(x) và (d₂): y = f₂(x)
• Bước 2: Phương trình hoành độ giao điểm: f₁(x₀) = f₂(x₀)
• Bước 3: Giải phương trình tìm được x₀. Suy ra y₀.

Tìm được A(x₀; y₀)

Để tăng hiệu quả học tập, các em hãy kết hợp việc chép phần lý thuyết trên với việc học qua video bài giảng dưới đây nha.

Giải bài tập đồ thị hàm số y = ax + b tập sách giáo khoa

Bài 15 – trang 51 (SGK Toán 9 Tập 1)

a) Vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ.

y = 2x; y = 2x + 5; y = -2/3x và y = -2/3x + 5

b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không? Vì sao ?

Hướng dẫn giải:

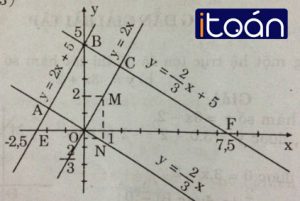
• Cho x = 1 => y = 2.1 = 2 ta được M(1; 2).

• Cho x = -2,5 => y = 2(-2,5) + 5 = 0 ta được E(-2,5; 0).
• Cho x = 0 => y = 5 ta được B(0; 5).

Với hàm số y = (-2/3)x:

• Cho x = 1 => y = (-2/3).1 = -2/3 ta được N(1;-2/3)

Với hàm số y = (-2/3x + 5)

• Cho x = 0 => y = 5 ta được B(0;5)
• Cho y = 0 => x = 7,5 ta được F(7,5;0)

Sau khi đã tính được các điểm M(1;2), E(-2,5;0), B(0;5), N(1;-2/3), F(7,5;0), các em sẽ tiến hành dựng các điểm đó trên mặt phẳng tọa độ lần lượt theo các bước sau:

b) Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.

Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x, đường thẳng (-2/3x) + 5 song song với đường thẳng y = -2/3x.

=> Tứ giác OABC là hình bình hành (có hai cặp cạnh song song).

Bài 16 – trang 51 (SGK Toán 9 Tập 1)

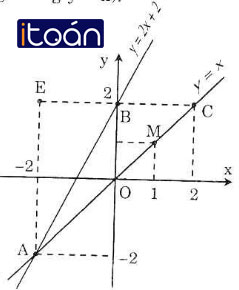
a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.

Hướng dẫn giải:

a)

Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.

Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.

b)

Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình: 2x + 2 = x => x = -2 => y = -2

Suy ra tọa độ giao điểm là A(-2; -2).

c)

Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.

• Tọa độ điểm C:

Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình: x = 2 => y = 2 => tọa độ C(2;2).

Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC).

Bài 17 – trang 51 (SGK Toán 9 Tập 1)

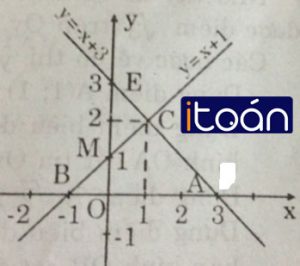
a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x +3 trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)

Hướng dẫn giải:

a)

• Với hàm số y = x + 1:

Cho x = 0 => y = 1 ta được M(0; 1).

Cho y = 0 => x + 1 = 0 => x = -1 ta được B(-1; 0).

Nối MB ta được đồ thị hàm số y = x + 1.

• Với hàm số y = -x + 3:

Cho x = 0 => y = 3 ta được E(0; 3).

Cho y = 0 => -x + 3 = 0 => x = 3 ta được A(3; 0).

Nối EA ta được đồ thị hàm số y = -x + 3.

b)

Từ hình vẽ ta có:

– Đường thẳng y = x + 1 cắt Ox tại B(-1; 0).

– Đường thẳng y = -x + 3 cắt Ox tại A(3; 0).

– Hoành độ giao điểm C của 2 đồ thị hàm số y = x + 1 và y = -x + 3 là nghiệm phương trình:

x + 1 = -x + 3

=> x = 1 => y = 2

=> Tọa độ C(1; 2)

c)

Ta có: AB = 3 + 1 = 4

Bài 18 – trang 51 (SGK Toán 9 Tập 1)

a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị B vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với giá trị a tìm được

Hướng dẫn giải:

a) Thay x = 4 và y = 11 vào y = 3x + b ta được: 11 = 3.4 + b = 12 + b

=> b = 11 – 12 = -1

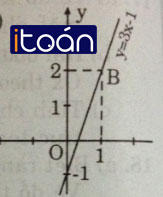
Ta được hàm số y = 3x – 1

• Cho x = 0 => y = -1 được A(0; -1)
• Cho x = 1 => y = 2 được B(1; 2).

Nối A, B ta được đồ thị hàm số y = 3x – 1.

b)

Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có: 3 = a(-1) + 5

=> a = 5 – 3 = 2

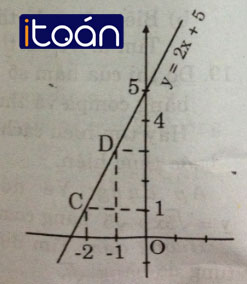
Ta được hàm số y = 2x + 5.

• Cho x = -2 => y = 1 được C(-2; 1)
• Cho x = -1 => y = 3 được D(-1; 3)

Nối C, D ta được đồ thị hàm số y = 2x + 5.

Bài 19 – trang 52 (SGK Toán 9 Tập 1)

Đồ thị của hàm số y = √3 x + √3 được vẽ bằng compa và thước thẳng (h.8).

Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.

Áp dụng: Vẽ đồ thị của hàm số y = √5 x + √5 bằng compa và thước thẳng.

Hướng dẫn: Tìm điểm trên trục tung có tung độ bằng √5.

Hướng dẫn giải:

a)

Cho x = 0 => y = √3 ta được (0; √3).

Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).

Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.

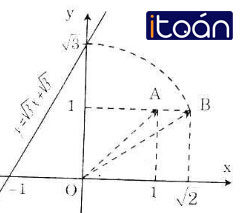
Các bước vẽ đồ thị y = √3 x + √3 như sau:

Bước 1: Dựng điểm A(1; 1) được OA = √2.

Bước 2: Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.

Bước 3: Dựng điểm B(√2; 1) được OB = √3.

Bước 4: Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3

Bước 5: Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.

b)

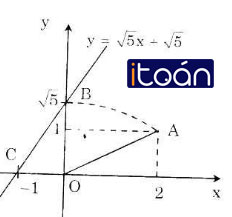
Áp dụng vẽ đồ thị hàm số y = √5 x + √5

• Cho x = 0 => y = √5 ta được (0; √5).
• Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).

Ta phải tìm điểm trên trục tung có tung độ bằng √5.

Cách vẽ:

Bước 1: Dựng điểm A(2; 1) ta được OA = √5.

Bước 2:  Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

Bài tập tự luyện Đồ thị hàm số y = ax + b

Câu 1: Đồ thị y=-5x không đi qua điểm

A. M (1;5)

B. N (-2;10)

C. P (-1;5)

D. Q (2;-10)

Câu 2: Đồ thị Đồ thị của hàm số y=ax (a≠0) là:

A. Một đường thẳng

B. Đi qua gốc tọa độ

C. Một đường thẳng đi qua gốc tọa độ

D. Một đoạn thẳng đi qua gốc tọa độ

Câu 3: Cho hàm số y=(2m–1)x + m. Tìm m để đồ thị hàm số qua gốc tọa độ

A. m=0

B. m=1

C. m=2

D. m=3

Câu 4: Cho đường thẳng d xác định bởi y=2x+1. Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành có phương trình là?

A. y= -2x-1

B. y= 2x-1

C. y= 2x+1

D. y= -2x+1

Đáp án bài tập tự luyện đồ thị hàm số y = ax + b

Câu 1. A

Câu 2. C

Câu 3. D

Câu 4. A

Kết luận

Vậy là bài học về hàm số y = ax + b đến đây là kết thúc. Vì bài này rất quan trọng nên các em hãy chịu khó đọc lại bài cẩn thận và làm toàn bộ bài tập trong sách giáo khoa lẫn sách bài tập để nâng cao trình độ nhé.

Xem thêm: 

• Thu thập số liệu thống kê tần số – Bài tập và Lời giải SGK Toán 7
• Số trung bình cộng là gì? – Bài tập & Lời giải SGK Toán 7
• Định lý pytago – Hướng dẫn giải bài tập Hình học lớp 7