Tính chất đường trung tuyến của tam giác – Toán 7

Trung điểm là điểm nằm chính giữa của một đoạn thẳng, vậy trung tuyến là gì nhỉ? Tiết học hôm nay chúng ta cùn tìm hiểu về đường trung tuyến nhé. Bài giảng: Tính chất đường trung tuyến của tam giác– Bài tập & lời giải thuộc chương trình Toán lớp 7, được các thầy cô giáo của iToan biên soạn bám sát với sách giáo khoa, thêm vào đó là các bài tập giúp học sinh tự luyện tập tại nhà. Mời các em học sinh và quý vị phụ huỳnh tham khảo!
Nội dung lý thuyết Tính chất đường trung tuyến của tam giác
-
-
-
- Đường trung tuyến của một tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện.
-
-
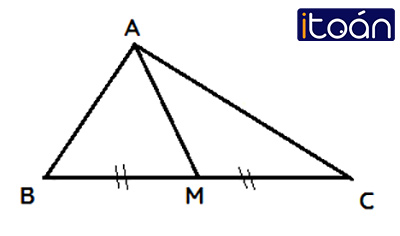
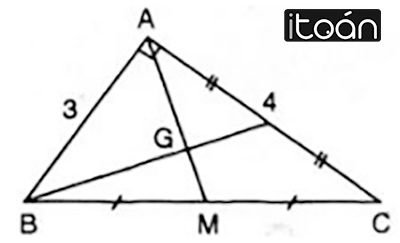
Ví dụ:
Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC. Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.
-
-
-
- Mỗi tam giác có ba đường trung tuyến.
-
-
Tính chất ba đường trung tuyến của tam giác
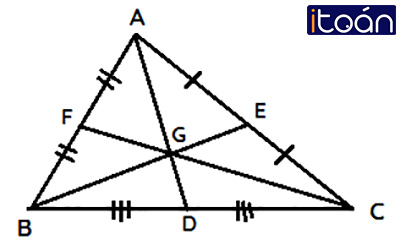
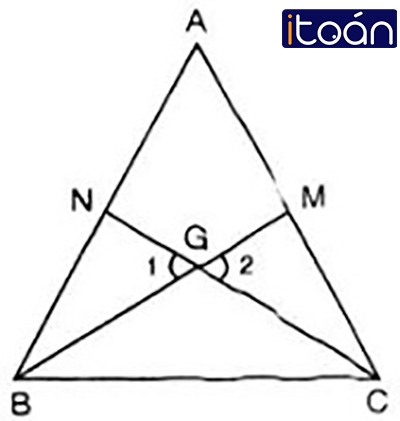
Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
Định lý 2: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 23 độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ: Với G là trọng tâm của ΔABC ta có:
AG=23AD;BG=23BE;CG=23CF.
Giải bài tập sách giáo khoa trang 66 Tính chất ba đường trung tuyến của tam giác
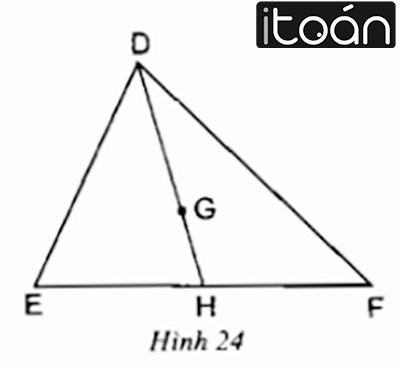
Bài 23- Trang 66 SGK Toán 7:
Cho điểm G là trọng tâm tam giác DEF đường trung tuyến của tam giác là DH. Trong các khẳng định dưới đây, khẳng định nào là đúng ?
DG/DH=1/2; DGGH=3
GH/DH=1/3; GH/DG=2/3
Bài Làm:
G là trọng tâm của tam giác DEF với DH là đường trung tuyến . Ta có:
GD/DH=2/3⇒GH/DH=1/3
Vậy khẳng định GH/DH=1/3 là đúng và các khẳng định còn lại sai.
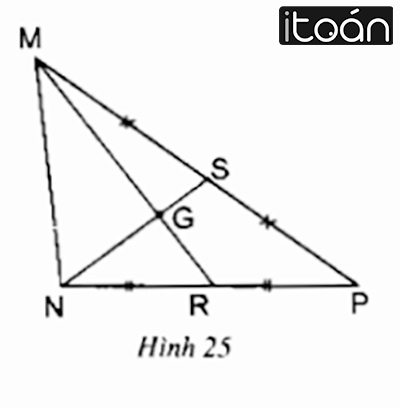
Bài 24- Trang 66 SGK Toán 7
Dựa vào hình 25 dưới đây để điền số thích hợp vào chỗ trống :
a) MG = … MR; GR = … MR; GR = … MG
b) NS = … NG; NS = … GS; NG = … GS
Bài Làm:
Nhìn vào hình vẽ ta thấy MR và NS là hai đường trung tuyến cắt nhau tại G suy ra G là trọng tâm của tam giác.
Do đó ta điền được số như sau:
a) MG=2/3.MR;GR=1/3.MR;GR=1/2.MG
b) NS=2/3.NG;NS=3GS;NG=2GS
Bài 25- Trang 67 SGK Toán 7
Định lý: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Dựa vào định lý này, hãy giải bài toán sau:
Cho tam giác vuông ABC có hai góc vuông AB = 3cm, AC= 4cm. Tính khoảng cách từ trọng tâm G tới đỉnh A của tam giác ABC.
Bài Làm:
Áp dụng định lí Pitago cho ΔABC vuông tại A, ta có:
BC2=AB2+AC2=32+42=25
⇒BC=5cm
Gọi M là trung điểm của BC và G là trọng tâm của ΔABC.
Vì AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM=12BC.
Vì G là trọng tâm của ∆ ABC nên AG=23AM⇒AG=23.12.BC
⇒AG=13.BC=13.5≈1.7cm
Bài 26: Trang 67 – SGK Toán 7
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Bài Làm:
ΔABC cân tại A => AB = AC.
Gọi M, N lần lượt là hai trung điểm của cạnh AB và AC, suy ra:
AN = BN = AM = CM (=12 AB = 12 AC)
Xét ΔBAM và ΔCAN có:
-
- Góc A chung
- AB = AC
- AM = AN
=> ΔBAM = ΔCAN (c.g.c) => BM = CN (đpcm)
Bài 27: Trang 67 – SGK Toán 7
Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Bài Làm:
Vẽ ΔABC. Gọi M, N lần lượt là trung điểm của AC và AB và gọi G là trọng tâm của tam giác.
Theo đề bài: CN = BM.
Vì G là trọng tâm tam giác ABC nên: CG = 23 CN; BG = 23 BM.
Suy ra: CG = BG.
Ta có: NG = CN – CG = BM – BG = GM.
Xét tam giác BGN và CGM có:
CG = BG (cmt)
G1ˆ=G2ˆ (đối đỉnh)
NG = GM (cmt)
⇒ΔBGN=ΔCGM(c−g−c)
⇒BN=CM
Mà M, N là trung điểm AB, AC nên AB = AC.
Vậy tam giác ABC cân tại A.
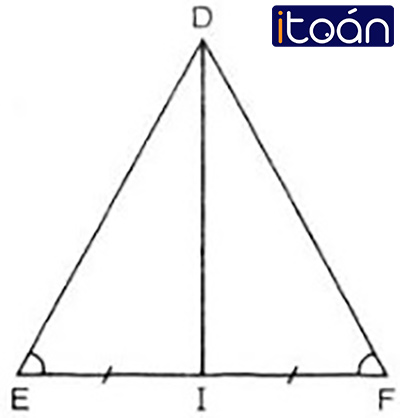
Bài 28: Trang 67 – SGK Toán 7
Cho tam giác cân DEF cân tại D và DI là đường trung quyến.
a) Chứng minh ΔDEI = ΔDFI.
b) Các góc DIE và góc DIF là góc gì?
c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đoạn DI.
Bài Làm:
a) Xét ΔDEI và ΔDFI có:
-
- DE = DF (ΔDEF cân)
- DI là cạnh chung.
- IE = IF (DI là trung tuyến)
=> ΔDEI = ΔDFI (c.c.c)
b) Vì ∆DEI = ∆DFI => DIEˆ=DIFˆ
mà DIEˆ+DIFˆ=1800 ( kề bù)
nên DIEˆ=DIFˆ=900
c) I là trung điểm của EF nên IE = IF = 5cm.
ΔDIE vuông tại I => DE2=DI2+EI2 (định lí Pitago)
=> DI2=132–52=144
=> DI=12.
Bài 29: Trang 67 – SGK Toán 7
Cho tam giác đều ABC có G là trọng tâm. Chứng minh rằng: GA = GB = GC
Hướng dẫn: Áp dụng định lí đã chứng minh ở bài tập 26.
Bài Làm:
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA = 23AM; GB = 23BN; GC = 23CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC
Bài 30: Trang 67 – SGK Toán 7
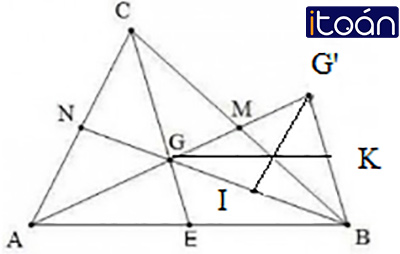
Cho tam giác ABC có trọng tâm G. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.
a) So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.
Bài Làm:
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA = 
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ = 
Vì G là trọng tâm của ∆ABC => GB = 
Mặt khác : GM = 
AG = GG’ (gt)
GM = 
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
=> BG’ = CG
mà CG = 
=> BG’ = 
Vậy mỗi cạnh của ∆BGG’ bằng 
b) So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG’
mà M là trung điểm của BC nên BM = 
Vì IG = 
GN = 
=> IG = GN
Do đó ∆IGG’ = ∆NGA (cgc) => IG’ = AN => IG’ =
– Gọi K là trung điểm BG => GK là trung tuyến ∆BGG’
Vì GE = 
=> GE = 
mà K là trung điểm BG’ => KG’ = EG
Vì ∆GMC = ∆G’BM (chứng minh trên)
=> 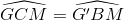
=> CE // BG’ => 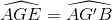
Do đó ∆AGE = ∆GG’K (cgc) => AE = GK
mà AE = 

Vậy mỗi đường trung tuyến ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó
Câu hỏi tự luyện Tính chất ba đường trung tuyến của tam giác
Phần câu hỏi
Câu 1: Chọn phát biểu sai:
A. Trọng tâm của tam giác cách đều ba cạnh của tam giác đó.
B. Ba đường trung tuyến của một tam giác luôn đi qua 1 điểm.
C. Đường nối 1 đỉnh của tam giác với trung điểm của cạnh đối diện được gọi là trung tuyến của tam giác.
D. Trọng tâm tam giác chia đường trung tuyến thành 2 đoạn thẳng có tỉ lệ 2:1
Câu 2: Một tam giác có mấy đường trung tuyến:
A. 1
B. 2
C. 3
D. 4
Câu 3: Trọng tâm của tam giác là:
A. Giao điểm của ba đường phân giác
B. Giao điểm của ba đường trung tuyến
C. Giao điểm của ba đường trung trực
Phần đáp án
1.A 2.C 3.B
Lời kết
Bài giảng:Tính chất ba dường trung tuyến của tam giác kết thúc tại đây. Sau bài học này, các em cần nhớ: Khái niệm và tính chất 3 đường trung tuyến, mọt số định lý và áp dụng vđịnh lý, tính chất vào giải toán. Để theo dõi và ôn tập Toán lớp 7, hãy truy cập Toppy. Toppy là nền tảng học trực tuyến với đầy đủ các bài học bám sát theo chương trình học trên lớp, sẽ giúp học sinh hiểu bài và nâng cao kiến thức.
Chúc em học tốt!
>> Xem thêm: