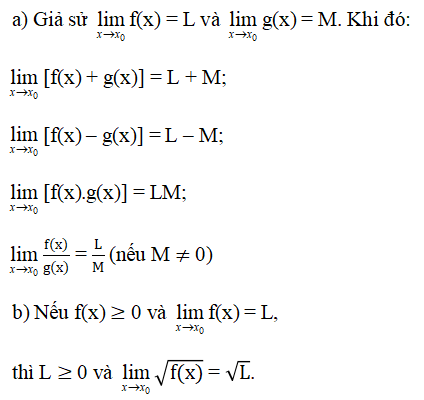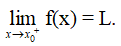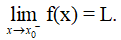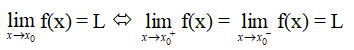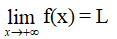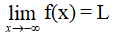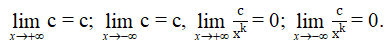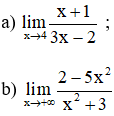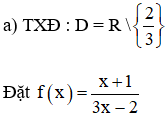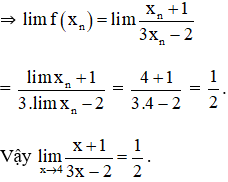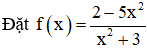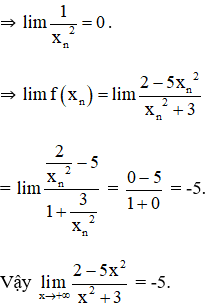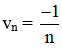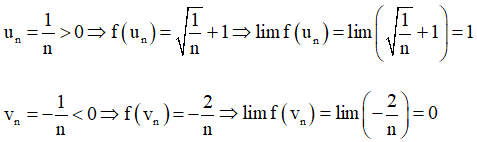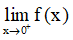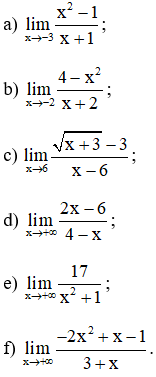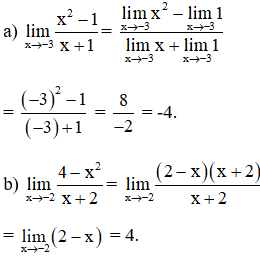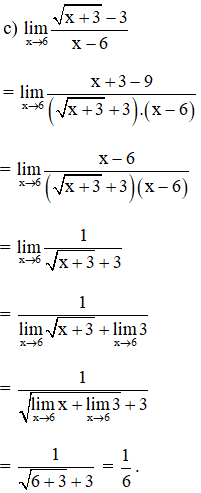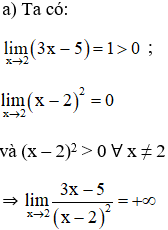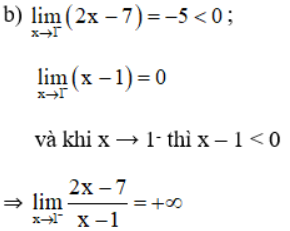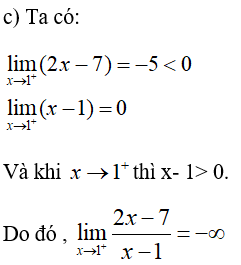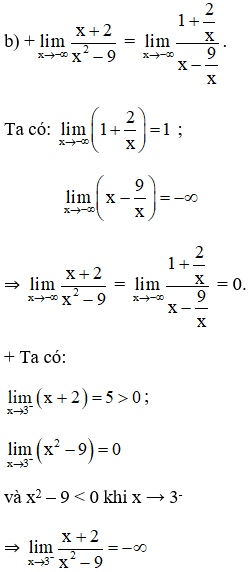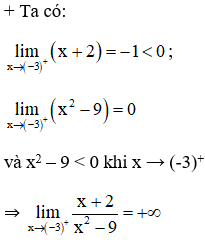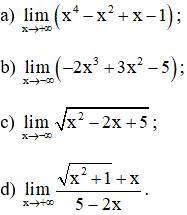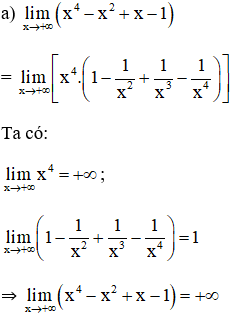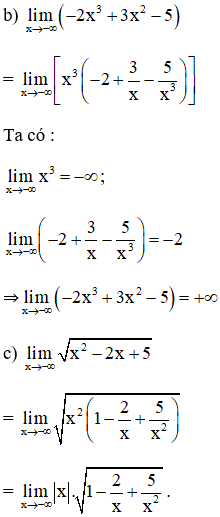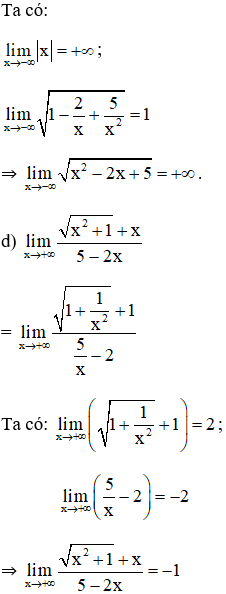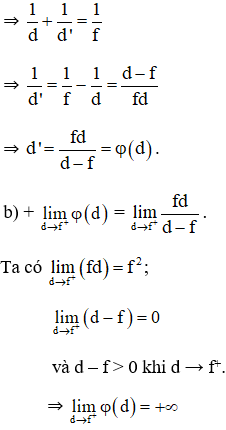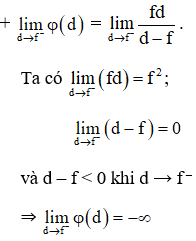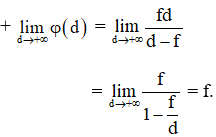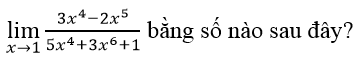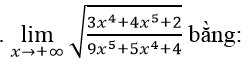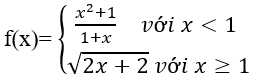Giới hạn của hàm số – Bài tâp & Lời giải Đại số 11
Xin chào các em đã đến với lớp học của iToan! Hôm nay, chúng ta sẽ cùng tìm hiểu bài: Giới hạn của hàm số– Bài tập & Lời giải Đại số 11. Bài giảng được các thầy cô giáo iToan biên soạn với phương pháp dạy logic, cụ thể, hy vọng sẽ giúp các em nắm bắt được bài một cách tốt nhất!
Mục tiêu bài giảng
Qua bài học này, các em cần nắm vững các phần kiến thức sau đây:
- Lý thuyết về giới hạn hàm số
- giải các bài tập SGK Đại số 11
- Thành thạo các bài tập tự luyện của iToan.
Lý thuyết Giới hạn của hàm số
Tổng hợp lý thuyết chi tiết & bổ ích nhất được iToan biên soạn, giúp cho các em có cái nhìn tổng quan và nền tảng về bài học!
Giới hạn hữu hạn của hàm số tại một điểm
1. Định nghĩa
Định nghĩa 1
Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \{x0} và xn → x0, ta có f(xn) → L.
Kí hiệu: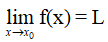 
hay f(x) → L khi x → x0.
Nhận xét: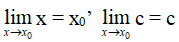 
với c là hằng số.
2. Định lí về giới hạn hữu hạn
Định lí 1
3. Giới hạn một bên
Định nghĩa 2
– Cho hàm số y = f(x) xác định trên (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.
Kí hiệu: 
– Cho hàm số y = f(x) xác định trên (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
Kí hiệu: 
Định lí 2
Giới hạn hữu hạn của hàm số tại vô cực
Định nghĩa 3
a) Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.
Kí hiệu: 
b) Cho hàm số y = f(x) xác định trên (–∞; a).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (xn) bất kì, xn < a và xn → –∞, ta có f(xn) → L.
Kí hiệu: 
Chú ý:
a) Với c, k là hằng số và k nguyên dương, ta luôn có:
b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi xn → +∞ hoặc x → –∞
Giải bài tập SGK Đại số 11 Giới hạn của hàm số
Bài 1 (trang 132 SGK Đại số 11):
Dùng định nghĩa tìm các giới hạn sau:
Lời giải:
Lấy dãy (xn) bất kì; xn ∈ D; lim xn = 4.
b) TXĐ: D = R.
Lấy dãy (xn) bất kì thỏa mãn xn → +∞
Bài 2 (trang 132 SGK Đại số 11):
Cho hàm số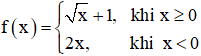 
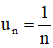
và các dãy số (un) với 
; (vn) với 
Tính limun, limvn, limf(un), limf(vn).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?
Lời giải:
Bài 3 (trang 132 SGK Đại số 11):
Tính các giới hạn sau:
Lời giải:
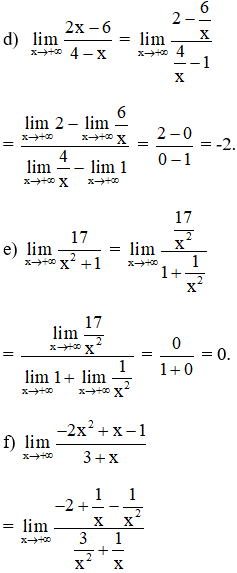
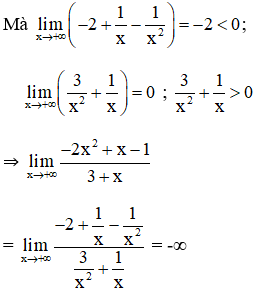
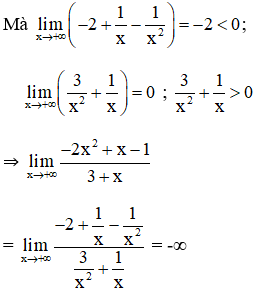
Bài 4 (trang 132 SGK Đại số 11): Tìm các giới hạn sau :
Lời giải:
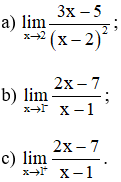
Bài 5 (trang 133 SGK Đại số 11):
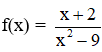có đồ thị như trên hình 53.a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x →- ∞,x →3–,x →-3+
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
Lời giải:
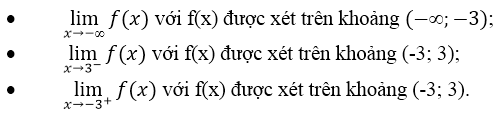
a) Quan sát đồ thị nhận thấy:
f(x) → 0 khi x → -∞
f(x) → -∞ khi x → 3-
f(x) → +∞ khi x → (-3)+.
Bài 6 (trang 133 SGK Đại số 11):
Tính:
Lời giải:
Bài 7 (trang 133 SGK Đại số 11):
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d‘ lần lượt là khoảng cách từ một vật thật AB và ảnh A‘B‘ của nó tới quang tâm O của thấu kính (hình dưới).
Lời giải:
a) Thấu kính hội tụ có tiêu cự f
⇒ Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở vô cùng.
⇒ Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và nằm ở vô cùng.
⇒ Ý nghĩa : Khi vật được đặt ở xa vô cùng thì sẽ cho ảnh tại tiêu điểm.
Bài tập tự luyện Giới hạn của hàm số
Phần câu hỏi
Câu 1:
A. 0 B. 2 C. 4 D. 6
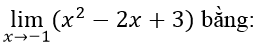
Câu 2:
A. 1/9 B. 3/5 C. (-2)/5 D. (-2)/3
Câu 3:
A. 0 B. √(1/3) C. √(3/5) D. 2/3
Câu 4:
A. +∞ B. 4 C. 0 D. -∞
Câu 5: Cho hàm số
Khi đó:
A. -1 B. 0 C. 1 D. +∞
Câu 15: Cho hàm số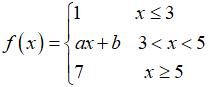 
. Xác định a; b để hàm số có giới hạn tại x = 3 và x = 5 .
Câu 20: Giá trị đúng của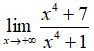 
là:
A. – 1
B. 1
C. 7
D. +∞
Câu 8: Tìm giới hạn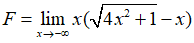 
:
A. +∞
B. -∞
C. 4/3
D. 0
Câu 9: Tìm a để hàm số sau có giới hạn khi x → 2:
.
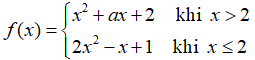
A. +∞
B. -∞
C. 1/2
D. 1
Câu 10: Cho hàm số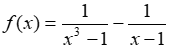 
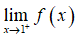
. Chọn kết quả đúng của 
:
A. -∞
B. -2/3
C. 2/3
D. +∞
