Hai tam giác bằng nhau – Học toán hình cùng itoan

Ở bài trước các em đã được tìm hiểu và luyện tập Tổng 3 góc của một tam giác. Hôm nay iToan sẽ cùng các em đi tìm hiểu về bài tiếp theo, đó là: Hai tam giác bằng nhau. Cùng tìm hiểu nhé!
Mục tiêu bài học ai tam giác bằng nhau
Dưới đây là 3 mục tiêu các em cần đạt được sau buổi học này:
- Nắm chắc và hiểu phần lý thuyết bài Hai tam giác bằng nhau.
- Chứng minh được hai tam giác bằng nhau dựa trên phần lý thuyết đã học.
- Hoàn thành các bài tập về hai tam giác bằng nhau để nâng cao và mở rộng kiến thức .
Bài giảng hai tam giác bằng nhau
1. Định nghĩa
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
2. Kí hiệu
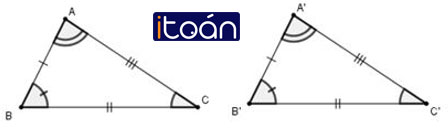
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết ΔABC = ΔA’B’C’
Người ta quy ước rằng khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự.
Ví dụ:
Trong đó A, A’ là hai đỉnh tương ứng, AB, A’B’ là hai cạnh tương ứng, ∠A, ∠A’ là hai góc tương ứng.
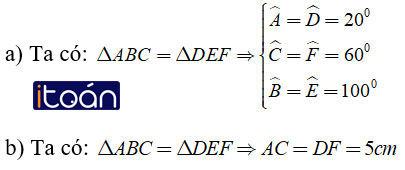
Ví dụ: Cho Δ ABC = ΔDEF
a) Biết ∠A = 20°, ∠C = 60°, ∠E = 100°. Tính số đó các góc của lại của mỗi tam giác?
b) Biết DF = 5cm có thể tìm độ dài các cạnh của tam giác ABC không?
Hướng dẫn giải:
Vậy ta chỉ được độ dài một cạnh của tam giác ABC là AC = 5cm.
Chứng minh hai tam giác bằng nhau là một trong những dạng bài tập phổ biến trong các kỳ thi cấp trung học cơ sở. Do đó, các em cần phải hiểu và nắm chắc phần kiến thức này. Các em hãy kết hợp việc học truyền thống và học qua video để hiểu bài nhanh chóng và củng cố kiến thức. Dưới đây là video bài giảng của cô giáo Yên Bình về bài học ngày hôm nay.
Bài tập SGK Hai tam giác bằng nhau
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 110:
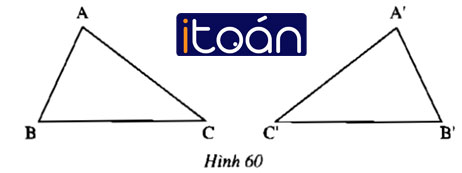
Cho hai tam giác ABC và A’B’C’ (hình 60)
Hãy dùng thước chia khoảng và thước đo góc để kiểm nghiệm rằng trên hình đó ta có:
AB = A’B’; AC = A’C’ ; BC = B’C’ ; ∠A = ∠A’ ; ∠B = ∠B’ ; ∠C = ∠C’
Hướng dẫn giải bài tập:
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 111:
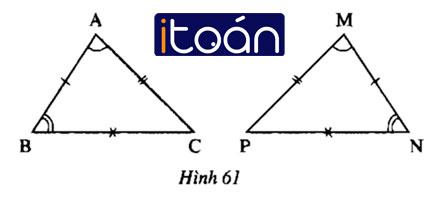
a) Cho hình 61. Hai tam giác ABC và MNP có bằng nhau hay không (Các cạnh hoặc các góc bằng nhau được đánh dấu bằng những kí hiệu giống nhau)? Nếu có, hãy viết kí hiệu về sự bằng nhau của hai tam giác đó
b) Hãy tìm: Đỉnh tương ứng với đỉnh A, góc tương ứng với góc N; cạnh tương ứng với cạnh AC
c) Điền vào chỗ trống (…): ΔABC =…; AC = …; ∠B = ⋯
Hướng dẫn giải bài tập:
a)
- Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
- Kí hiệu: ΔABC = ΔMNP
b)
- Đỉnh tương ứng với đỉnh A là đỉnh M
- Góc tương ứng với góc N là góc B
- Cạnh tương ứng với cạnh AC là cạnh MP
c)
ΔACB = ΔMPN;
AC = MP;
∠B = ∠N
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 111:
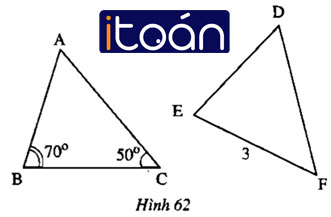
Cho ΔABC = ΔDEF (hình 62)
Tìm số đo góc D và độ dài cạnh BC
Hướng dẫn giải bài tập:
ΔABC = ΔDEF ⇒ ∠D = ∠A = 180o – 70o – 50o = 60o (hai góc tương ứng)
Và BC = EF ⇒ BC = 3cm (hai cạnh tương ứng)
Bài 10 (trang 111 SGK Toán 7 Tập 1)
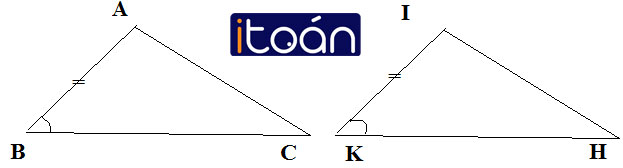
Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.
Hướng dẫn giải bài tập:
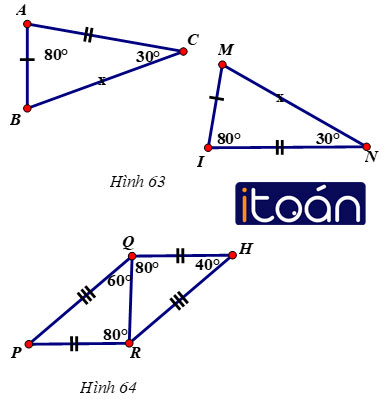
Xem hình 63
Ta có:
- ∠A = ∠I = 80o
- ∠C = ∠N = 30o
- ∠M = ∠B = 180o – (80o + 30o ) = 70o
- Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
ΔPQR có: ∠PQR + ∠QPR +∠PRQ = 180o => ∠QPR = 180o – 60o – 80o = 40o
ΔHQR có: ∠HQR + ∠QHR + ∠HRQ = 180o => ∠HRQ = 180o – 40o – 80o = 60o
Ta có:
- ∠HQR = ∠PQR = 80o
- ∠QHR = ∠QPR = 40o
- ∠QHR = ∠PQR
- Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
Bài 11 (trang 112 SGK Toán 7 Tập 1):
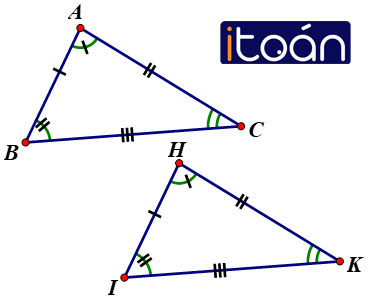
Cho tam giác ABC = tam giác HIK
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với góc H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.
Hướng dẫn giải bài tập:
a)
Vì tam giác ABC = tam giác HIK nên:
- Cạnh tương ứng với cạnh BC là IK.
- Góc tương ứng với góc H là góc A.
b)
- Các cạnh bằng nhau là: AB = HI, AC = HK, BC = IK
- Các góc bằng nhau là: ∠A = ∠H; ∠B = ∠I; ∠C = ∠K
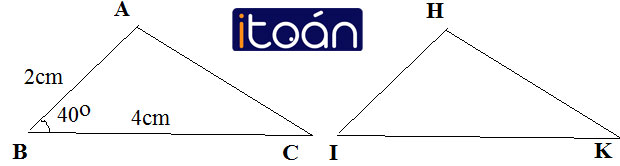
Bài 12 (trang 112 SGK Toán 7 Tập 1):
Cho tam giác ABC = tam giác HIK, trong đó ∠AB = 2cm , ∠góc B = 40o, ∠BC = 4cm. Em có thể suy ra số đo của những cạnh nào, những góc nào của tam giác HIK.
Hướng dẫn giải bài tập:
Ta có ΔABC = ΔHIK
Theo định nghĩa hai tam giác bằng nhau
HI = AB = 2cm
IK = BC = 4cm
∠I = ∠B = 40º
Bài 13 (trang 112 SGK Toán 7 Tập 1):
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
Hướng dẫn giải bài tập:
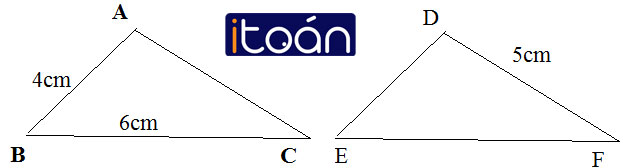
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Bài 14 (trang 112 SGK Toán 7 Tập 1):
Cho hai tam giác bằng nhau: tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một tam giác có ba đỉnh H, I, K. Viết kí hiệu về sự bằng nhau của hai tam giác đó biết AB = KI, góc B = góc K.
Hướng dẫn giải bài tập:
Ta có:
∠B = ∠K nên B, K là hai đỉnh tương ứng.
AB = KI nên A, I là hai đỉnh tương ứng.
Nên ΔABC = ΔIKH
Bài tập tự luyện Hai tam giác bằng nhau
Bài tập 1: Cho tam giác ADE bằng tam giác BAC. Cách viết nào đúng:
A. ΔDAE = ΔABC
B. ΔDEA = ΔBAC
C. ΔEDA = ΔCBA
D. ΔDEA = ΔABC
Bài tập 2: Cho tam giác ΔMNE=ΔDKI và MN=4cm,NE=5cm. Độ dài KI là :
A. 5cm
B. 4cm
C. 9cm
D. 6cm
Bài tập 3: Cho ΔABC = ΔDEF. Biết rằng AB = 6cm, AC = 8cm và EF = 10cm. Chu vi tam giác DEF là:
A. 24cm
B. 20cm
C. 18cm
D. 30cm
Bài tập 4: Cho ΔABC=ΔMNP. Biết AB = 5cm, MP = 7cm và chu vi của tam giác ABC bằng 22cm. Tính các cạnh còn lại của mỗi tam giác
A. NP = BC = 9cm
B. NP = BC = 11cm
C. NP = BC = 10cm
D. NP = 9cm;BC = 10cm
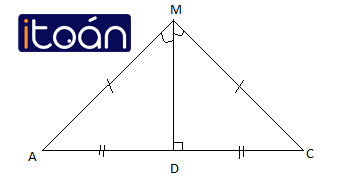
Bài tập 5: Cho hình vẽ sau, chọn kết luận “không” đúng:
A. ΔAMD = ΔDMC
B. ΔMAD = ΔMCD
C. ΔMAC = ΔMCA
D. ΔADM = ΔCDM
Hướng dẫn giải bài tập tự luyện Hai tam giác bằng nhau
Bài tập 1: A
Bài tập 2: A
Bài tập 3: A
Bài tập 4: C
Bài tập 5: A
Lời kết
Vậy là các em đã cùng với itoan hoàn thành xong buổi học ngày hôm nay. Nếu các em còn cảm thấy khúc mắc ở đâu, thì hãy nhắn tin ngay cho itoan để được hỗ trợ và giúp nhé! Chúc các em học tập thật tốt.
Xem thêm bài giảng: