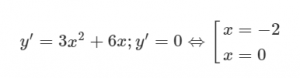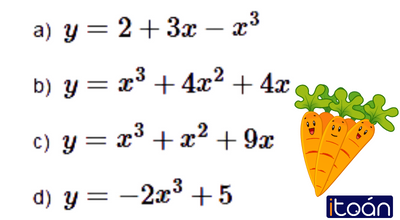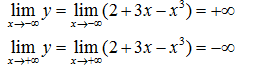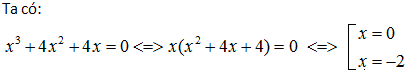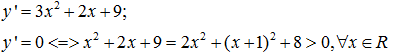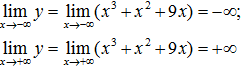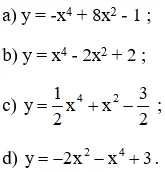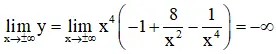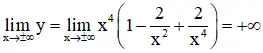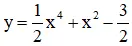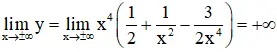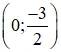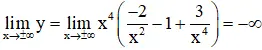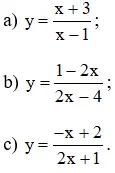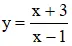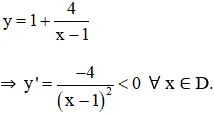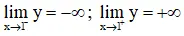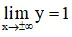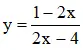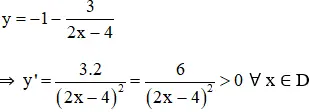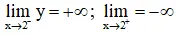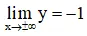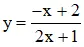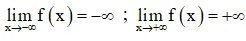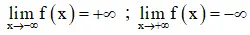Khảo sát sự biến thiên và vẽ đồ thị hàm số-Chinh phục giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị hàm số nằm trong những bài đầu của chương trình toán lớp 12. Đây là kiến thức cơ bản và quan trọng trong chương trình toán THPT nói chung và chương trình toán lớp 12 nói riêng. Học sinh cần phải nắm chắc cách khảo sát sự biến thiên và vẽ đồ thị hàm số để có thể học tốt chương trình toán 12, vì các chương sau của chương trình toán 12 sẽ áp dụng kiến thức về khảo sát sự biến thiên và vẽ đồ thị hàm số. Hôm nay itoan sẽ cùng bạn tìm hiểu cách khảo sát sự biến thiên và vẽ đồ thị hàm số đồng thời nắm chắc kiến thức hơn.
Mục tiêu bài học Khảo sát sự biến thiên và vẽ đồ thị hàm số
Sau khi học xong những bài học này, các bạn nhỏ cần nắm được các kiến thức, kĩ năng sau:
- Biết sơ đồ tổng quát để khảo sát hàm số: tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên và vẽ đồ thị hàm số.
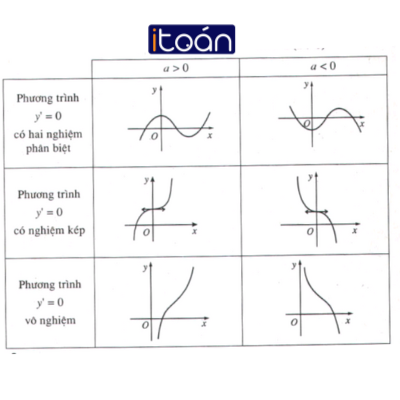
- Biết cách phân loại các dạng đồ thị hàm số.
- Biết cách khảo sát và vẽ đồ thị của các hàm số bậc ba.
- Biết cách phân loại các dạng đồ thị các hàm số trên.
Lý thuyết cần nắm bài Khảo sát sự biến thiên và vẽ đồ thị hàm số
Sau đây là những lý thuyết trọng tâm nhất được itoan biên soạn, giúp các bạn nắm vững bài học và tạo nền tảng giúp bé áp dụng giải các bài tập:
I. Sơ đồ khảo sát hàm số
1. Tập xác định
Tìm tập xác định của hàm số.
2. Sự biến thiên
- Xét chiều biến thiên của hàm số:
+ Tính đạo hàm;
+ Tìm các điểm tại đó đạo hàm bằng 0 hoặc không xác định;
+ Xét dấu đạo hàm và suy ra chiều biến thiên của hàm số.
- Tìm điểm cực trị.
- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có).
- Lập bảng biến thiên.
3. Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.
Chú ý:
- Nếu hàm số tuần hoàn với chu kì T thì chỉ cần khảo sát sự biến thiên và vẽ đồ thị trên một chu kì, sau đó tịnh tiến đồ thị song song với trục Ox.
- Nên tính thêm tọa độ một số điểm, đặc biệt là tọa độ các giao điểm của đồ thị với các trục.
- Nên lưu ý đến tính chẵn, lẻ của hàm số và tính đối xứng của đồ thị để vẽ cho chính xác.
II. Khảo sát một số hàm đơn thức và phân thức
1. Hàm số bậc ba y=ax3+bx2+cx+d(a≠0)
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y=x3+3x2−4
Giải
(1) Tập xác định: D=R
(2) Sự biến thiên
- Chiều biến thiên
Trên các khoảng (−∞;−2) và (0;+∞) , y′ dương nên hàm số đồng biến.
Trên khoảng (−2;0) âm nên hàm số nghịch biến.
- Cực trị
Hàm số đạt cực đại tại x=−2; yCD=y(−2)=0
Hàm số đạt cực tiểu tại x=0; yCT=y(0)=−4
- Các giới hạn tại vô cực
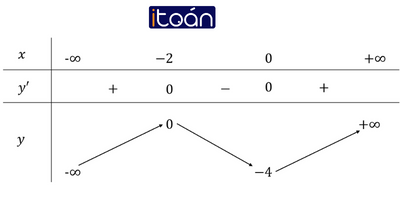
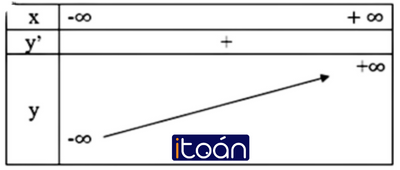
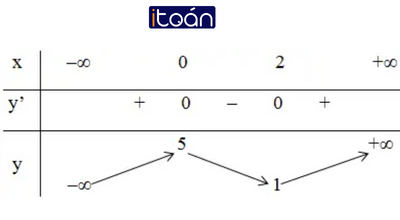
- Bảng biến thiên
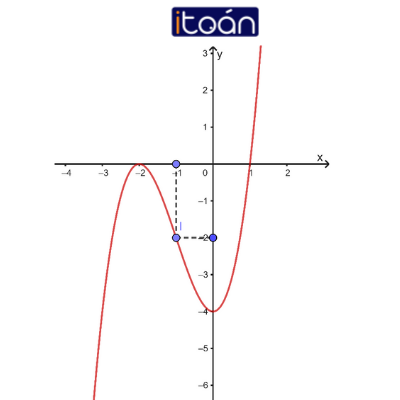
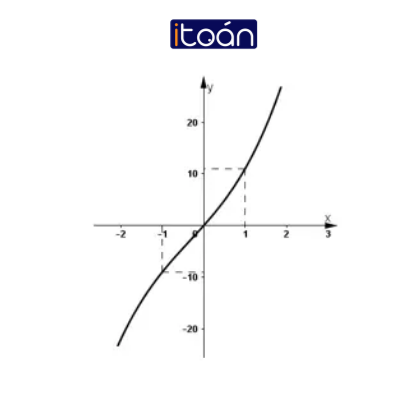
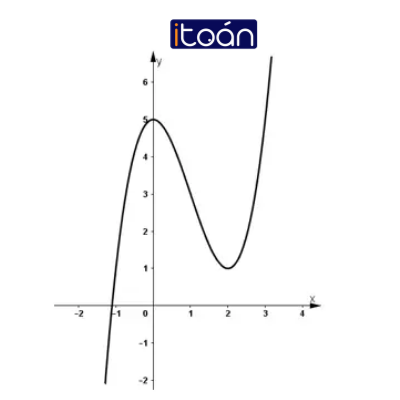
(3) Đồ thị
Ta có: x3+3x2−4=0⇔ x=−2; x=1
Vậy (−2;0) và (1;0) là các giao điểm của đồ thị với trục Ox.
Vì y(0)=−4 nên (−4;0) là giao điểm của đồ thị với trục Oy. Điểm đó cũng là điểm cực tiểu của đồ thị.
Chú ý: Đồ thị hàm số đã cho có tâm đối xứng là điểm I(−1;−2) . Hoành độ của điểm I là nghiệm của phương trình y′′=0
III. Sự tương giao giữa các đồ thị
1. Giao điểm của hai đồ thị
- Giả sử hàm số y=f(x) có đồ thị là C1 và hàm số y=g(x) có đồ thị là C2
- Để tìm hoành độ giao điểm của hai đồ thị trên là ta giải phương trình f(x)=g(x)
- Số nghiệm của phương trình trên bằng số giao điểm của hai đồ thị.
2. Sự tiếp xúc của hai đường cong
- Giả sử hàm số y=f(x) có đồ thị là C1 và hàm số y=g(x) có đồ thị là C2
- Hai đường cong C1 và C2 tiếp xúc nhau khi và chỉ khi hệ phương trình:
có nghiệm và nghiệm của hệ phương trình trên là hoành độ tiếp điểm của hai đường cong đó.
Các bạn có thể tham khảo video hướng dẫn bài học dưới đây!
Hướng dẫn giải bài tập Khảo sát sự biến thiên và vẽ đồ thị hàm số
Phần bài tập trong sách giáo khoa rất sát với lý thuyết nên các bạn cố gắng hoàn thành hết nhé!
Bài 1 trang 43 sách giáo khoa giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:
a) Tập xác định: R
Sự biến thiên:
Chiều biến thiên: y’ = 3 – ; y’=0 <=> 3 –
= 0 <=> x =-1 ( y=4) hoặc x =1 (y =0).
Trên các khoảng (-∞; -1) và (1; +∞), y’ âm nên hàm số nghịch biến. Trên khoảng (-1; 1), y’ dương nên hàm số đồng biến.
Cực trị:
Hàm đạt cực đại tại x =1 ; yCĐ = y (1) = 4.
Hàm số đạt cực tiểu tại x= 1-; yCT = y(-1) = 0.
Các giới hạn tại vô cực:
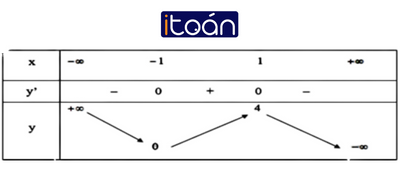
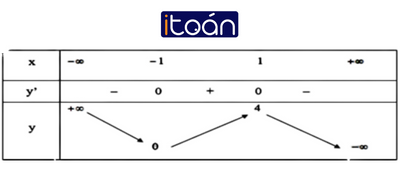
Bảng biến thiên:
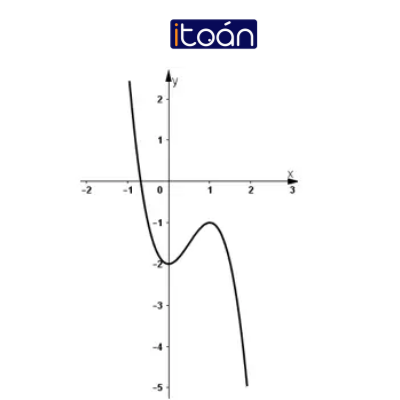
Vậy (-1; 0) và (2; 0) là các giao điểm của đồ thị với trục Ox.
y(0) = 2 nên (0; 2) là giao điểm của đồ thị với trục Oy.
b) Tập xác định: R.
Sự biến thiên:
Chiều biến thiên: y’ = + 8x+4
Cực trị
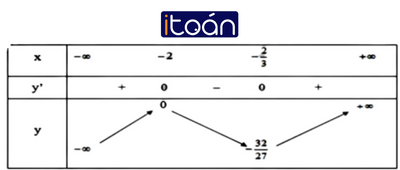
Bảng biến thiên:
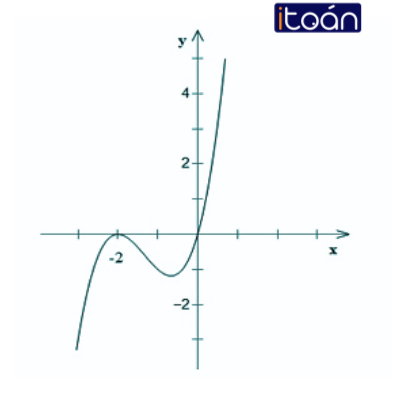
Đồ thị:
Vậy, (0; 0) và (-2; 0) là các giao điểm của đồ thị với trục Ox.
y(0) = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy.
Toạ độ một số điểm: (-3; -3); (-1; -1).
c) TXĐ : R
Sự biến thiên:
Chiều biến thiên:
Vậy, hàm số đồng biến trên R
Cực trị: Hàm số không có cực trị.
Các giới hạn tại vô cực:
Bảng biến thiên:
Đồ thị:
Vậy, (0; 0) là giao điểm của đồ thị với trục Ox.
y(0) = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy.
Đồ thị có tâm đối xứng là điểm có hoành độ là nghiệm của phương trình: y” = 0
Bài 2 (trang 43 SGK Giải tích 12)
Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
Lời giải:
a) Hàm số y = -x4 + 8x2 – 1.
1) Tập xác định: D = R
2) Sự biến thiên:
+ Chiều biến thiên:
y’ = -4x3 + 16x = -4x(x2 – 4)
y’ = 0 ⇔ -4x(x2 – 4) = 0 ⇔ x = 0 ; x = ±2
Trên khoảng (-∞; -2) và (0; 2), y’ > 0 nên hàm số đồng biến.
Trên các khoảng (-2; 0) và (2; +∞), y’ < 0 nên hàm số nghịch biến.
+ Cực trị :
Hàm số đạt cực đại tại x = 2 và x = -2 ; yCĐ = 15
Hàm số đạt cực tiểu tại x = 0 ; yCT = -1.
+ Giới hạn:
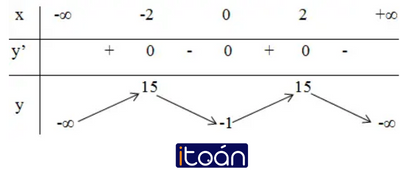
+ Bảng biến thiên:
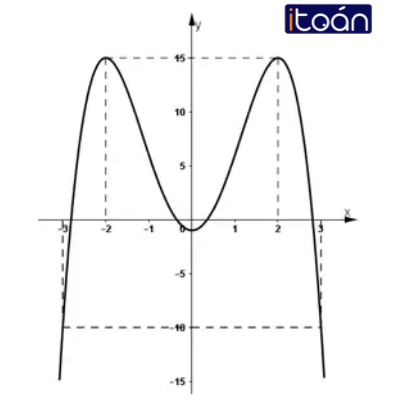
3) Đồ thị:
+ Hàm số đã cho là hàm số chẵn, vì:
y(-x) = -(-x)4 + 8(-x)2 – 1 = -x4 + 8x2 – 1 = y(x)
⇒ Đồ thị nhận Oy làm trục đối xứng.
+ Giao với Oy tại điểm (0; -1) (vì y(0) = -1).
+ Đồ thị hàm số đi qua (-3; -10) và (3; 10).
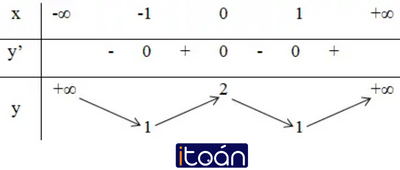
b) Hàm số y = x4 – 2x2 + 2.
1) Tập xác định: D = R
2) Sự biến thiên:
+ Chiều biến thiên:
y’ = 4x3 – 4x = 4x(x2 – 1)
y’ = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 ; x = ±1.
+ Giới hạn:
+ Bảng biến thiên:
Kết luận :
Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).
Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).
Đồ thị hàm số có điểm cực đại là: (0; 2)
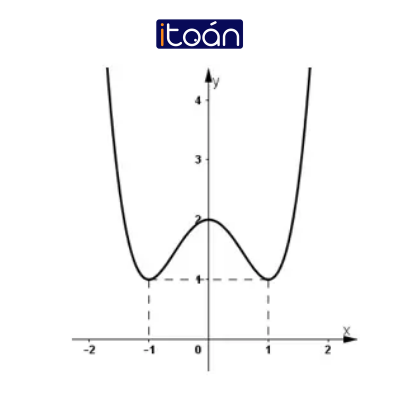
3) Đồ thị:
+ Hàm số chẵn nên đồ thị hàm số nhận trục Oy là trục đối xứng.
+ Đồ thị hàm số cắt trục tung tại (0; 2).
+ Đồ thị hàm số đi qua (-1; 1) và (1; 1).
+ Đồ thị hàm số:
c) Hàm số 
1) Tập xác định: D = R
2) Sự biến thiên:
+ y’ = 2x3 + 2x = 2x(x2 + 1)
y’ = 0 ⇔ 2x(x2 + 1) = 0 ⇔ x = 0
+ Giới hạn:
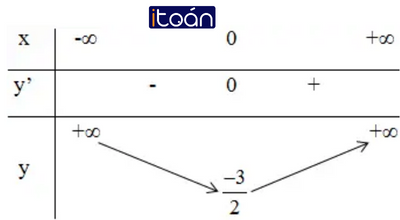
+ Bảng biến thiên:
Kết luận: Hàm số đồng biến trên khoảng (0; +∞).
Hàm số nghịch biến trên các khoảng (-∞; 0).
Đồ thị hàm số có điểm cực đại là: (0; -3/2).
3) Đồ thị:
+ Hàm số chẵn nên nhận trục Oy là trục đối xứng.
+ Hàm số cắt trục hoành tại điểm (-1; 0) và (1; 0).
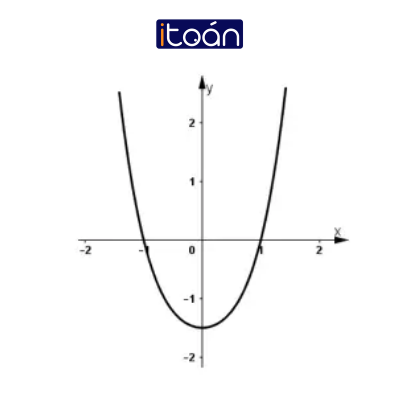
+ Hàm số cắt trục tung tại điểm
d) Hàm số y = -2x2 – x4 + 3.
1) Tập xác định: D = R
2) Sự biến thiên:
+ Chiều biến thiên:
y’ = -4x – 4x3 = -4x(1 + x2)
y’ = 0 ⇔ -4x(1 + x2) = 0 ⇔ x = 0
+ Giới hạn:
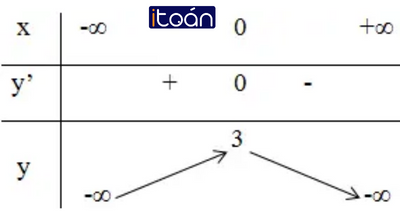
+ Bảng biến thiên:
Kết luận: Hàm số đồng biến trên khoảng (-∞; 0).
Hàm số nghịch biến trên các khoảng (0; +∞).
Đồ thị hàm số có điểm cực đại là: (0; 3).
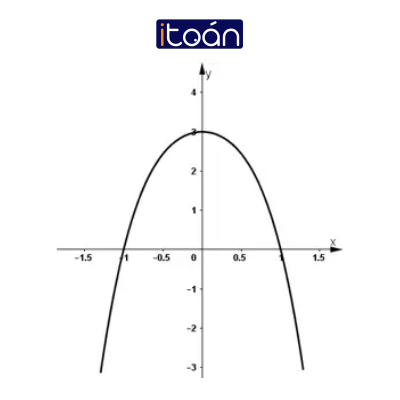
3) Đồ thị:
+ Hàm số là hàm số chẵn nên nhận trục Oy là trục đối xứng.
+ Hàm số cắt trục Ox tại (-1; 0) và (1; 0).
+ Hàm số cắt trục Oy tại (0; 3).
Bài 3 (trang 43 SGK Giải tích 12)
Khảo sát sự biến thiên và vẽ đồ thị các hàm số phân thức:
Lời giải:
a) Hàm số 
1) Tập xác định: D = R \ {1}
2) Sự biến thiên:
+ Chiều biến thiên:
⇒ Hàm số nghịch biến trên (-∞; 1) và (1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
⇒ x = 1 là tiệm cận đứng.
⇒ y = 1 là tiệm cận ngang.
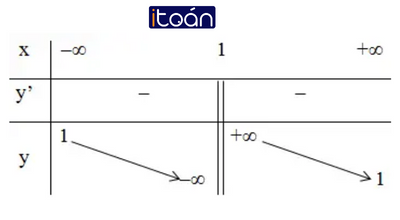
+ Bảng biến thiên:
3) Đồ thị:
+ Giao với Oy: (0; -3)
+ Giao với Ox: (-3; 0)
+ Đồ thị nhận (1; 1) là tâm đối xứng.
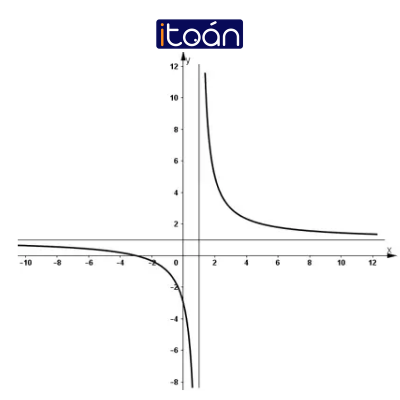
b) Hàm số 
1) Tập xác định: D = R \ {2}
2) Sự biến thiên:
+ Chiều biến thiên:
⇒ Hàm số đồng biến trên (-∞; 2) và (2; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
⇒ x = 2 là tiệm cận đứng của đồ thị hàm số.
⇒ y = -1 là tiệm cận ngang.
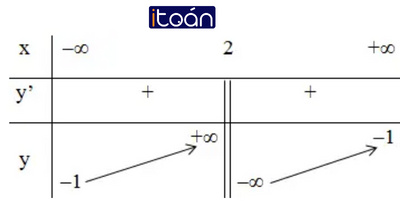
+ Bảng biến thiên:
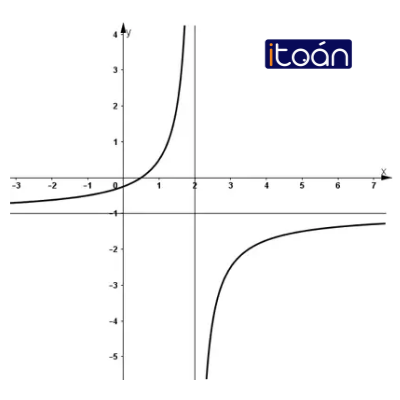
3) Đồ thị:
+ Giao với Oy: (0; -1/4)
+ Giao với Ox: (1/2; 0)
+ Đồ thị hàm số nhận (2; -1) là tâm đối xứng.
số
Bài 4 (trang 44 SGK Giải tích 12)
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
a) x3 – 3x2 + 5 = 0 ;
b) -2x3 + 3x2 – 2 = 0 ;
c) 2x2 – x4 = -1
Lời giải:
a) Xét y = f(x) = x3 – 3x2 + 5 = 0 (1)
– TXĐ: D = R
– Sự biến thiên:
+ Chiều biến thiên:
f'(x) = 3x2 – 6x = 3x(x – 2)
f'(x) = 0 ⇔ x = 0 ; x = 2
+ Giới hạn:
+ Bảng biến thiên:
– Đồ thị:
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất.
⇒ phương trình x3 – 3x2 + 5 = 0 chỉ có 1 nghiệm duy nhất.
b) Xét hàm số y = f(x) = -2x3 + 3x2 – 2.
– TXĐ: D = R
– Sự biến thiên:
+ Chiều biến thiên:
y’ = -6x2 + 6x = -6x(x – 1)
y’ = 0 ⇔ x = 0 ; x = 1
+ Giới hạn:
+ Bảng biến thiên:
– Đồ thị:
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất
⇒ phương trình f(x) = 0 có nghiệm duy nhất.
Vậy phương trình -2x3 + 3x2 – 2 = 0 chỉ có một nghiệm.
Lời kết
Bài học khảo sát sự biến thiên và đồ thị hàm số đã khép lại tại đây. Hy vọng với bài giảng chi tiết, dễ hiểu trên, các bạn đã nắm vững được kiến thức và áp dụng được linh hoạt trong tình huống thực tế. Ngoài ra, các bạn có thể truy cập vào trang web Toppy. Với đội ngũ giảng viên tâm huyết, nhiệt tình, Toppy luôn sẵn sàng giúp đỡ khi con gặp bất kì khó khăn nào trong học tập. Chúc các bạn luôn học tập tốt!
Xem thêm một số bài giảng liên quan khác tại đây: