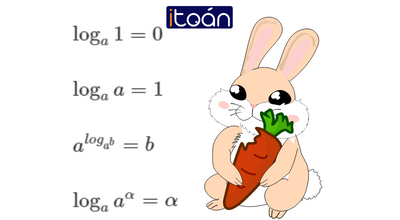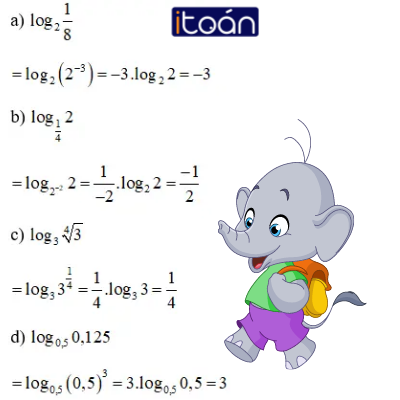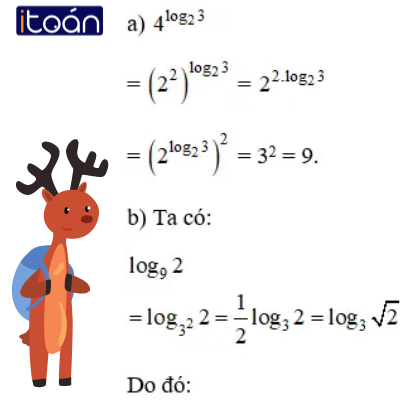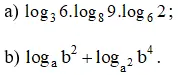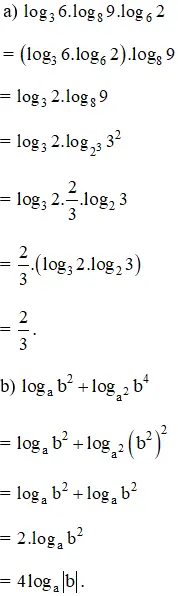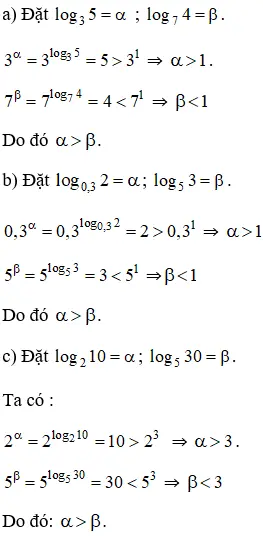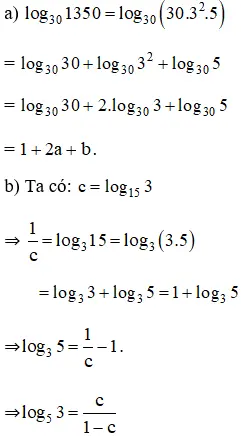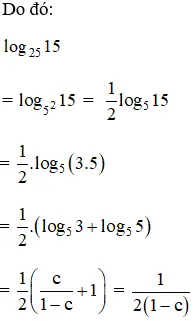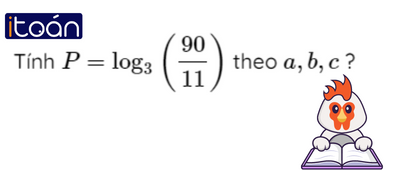Logarit – Tổng hợp kiến thức và bài tập – Giải tích lớp 12 itoan

Điểm nhấn tạo nên sự thú vị của chương trình lớp 12 là sự “góp mặt” của phần các công thức logarit bao gồm công thức mũ logarit, đạo hàm logarit, logarit cơ số e,… Hay thì hay thật đó nhưng phần kiến thức này cũng khiến khá nhiều bạn học sinh gặp khó khăn trong việc chinh phục để đạt được điểm cao trong các kì thi lớp 12. Vậy thì hãy cùng itoan đến với bài học hôm nay để giải đáp những thắc mắc này ngay thôi nào!
Mục tiêu bài học Khảo sát sự biến thiên và vẽ đồ thị hàm số
Sau khi học xong những bài học này, các bạn nhỏ cần nắm được các kiến thức, kĩ năng sau:
- Biết khái niệm logarit cơ số a (a > 0, a≠1) của một số dương
- Biết các tính chất của logarit (so sánh hai lôgarit cùng cơ số, qui tắc tính lôgarit, đổi
cơ số lôgarit) - Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản
- Biết vận dụng các tính chất của logarit vào các bài tập biến đổi, tính toán các biểu thức chứa logarit
Lý thuyết cần nắm bài Khảo sát sự biến thiên và vẽ đồ thị hàm số
Sau đây là những lý thuyết trọng tâm nhất được itoan biên soạn, giúp các bạn nắm vững bài học và tạo nền tảng giúp bé áp dụng giải các bài tập:
I. Khái niệm logarit
1. Định nghĩa
Cho hai số dương a,b với a≠1 . Số thực α thỏa mãn đẳng thức aα=b được gọi là logarit cơ số a của b và kí hiệu là logab.
α=logab⇔aα=b
Chú ý: Không có lôgarit của số âm và số 0.
2. Tính chất
Cho hai số dương a,b với a≠1 và α∈R, ta có:
II. Quy tắc tính logarit
1. Lôgarit của một tích
Định lí 1: Cho ba số dương a,b1,b2 với a≠1, ta có:
loga(b1b2)=logab1 + logab2
Logarit của một tích bằng tổng các logarit.
Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương.
Cho b1,b2,...,bn>0,a>0,a≠1, ta có:
loga(b1b2…bn)=logab1 + logab2+…+logabn
2. Logarit của một thương
Định lí 2: Cho ba số dương a,b1,b2 với a≠1, ta có:
3. Lôgarit của một lũy thừa
Định lí 3: Cho hai số dương a,b , a≠1 . Với mọi α ta có:
III. Đổi cơ số
Hướng dẫn giải bài tập Khảo sát sự biến thiên và vẽ đồ thị hàm số
Phần bài tập trong sách giáo khoa rất sát với lý thuyết nên các bạn cố gắng hoàn thành hết nhé!
Bài 1 (trang 68 SGK Giải tích 12): Không sử dụng máy tính, hãy tính:
Hướng dẫn giải:
Bài 2 (trang 68 SGK Giải tích 12): Tính
Hướng dẫn giải:
Bài 3 (trang 68 SGK Giải tích 12): Rút gọn biểu thức:
Hướng dẫn giải:
Bài 4 (trang 68 SGK Giải tích 12): So sánh các cặp số sau:
Hướng dẫn giải:
Bài 5 (trang 68 SGK Giải tích 12):
a) Cho a = log303; b = log305
Hãy tính log301350 theo a, b.
b) Cho c = log153. Hãy tính log2515 theo c.
Hướng dẫn giải:
Bài tập tự luyện Logarit
Bài tập 1: Cho a và b là hai số thực dương thỏa mãn a3b2=32. Giá trị của 3log2a+2log2b bằng:
A. 4
B. 5
C. 2
D. 32
Bài tập 2: Cho log35=a, log36=b, log322=c.
A. P = 2a−b+c
B. P = 2a+b+c
C. P = 2a+b−c
D. P = a+2b−c
Bài tập 3: Cho log303=a;log305=b. Tính log301350 theo a,b ;log301350 bằng:
A. 2a+b
B. 2a+b+1
C. 2a+b−1
D. 2a+b−2
Đáp án
Bài tập 1: B
Bài tập 2: D
Bài tập 3: B
Lời kết sau bài học Logarit
Bài học Logarit đã khép lại tại đây. Hy vọng với bài giảng chi tiết, dễ hiểu trên, các bạn đã nắm vững được kiến thức và áp dụng được linh hoạt trong tình huống thực tế. Ngoài ra, các bạn có thể truy cập vào trang web Toppy. Với đội ngũ giảng viên tâm huyết, nhiệt tình, Toppy luôn sẵn sàng giúp đỡ khi con gặp bất kì khó khăn nào trong học tập. Chúc các bạn luôn học tập tốt!
Xem thêm một số bài giảng liên quan khác tại đây: