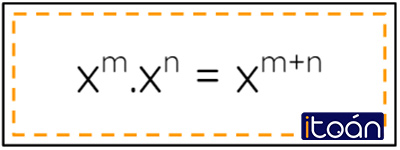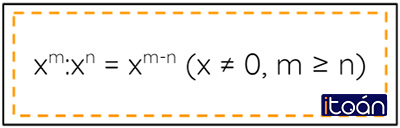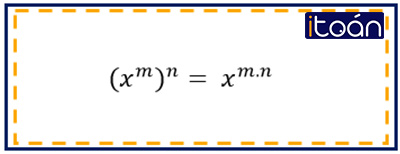Lũy thừa của số hữu tỉ – Bài tập & Lời giải SGK Toán 7

2.3/5 - (38 bình chọn)

Ở Toán lớp 6, các em đã được học về Lũy thừa của số tự nhiên. Trong chương trình Toán lớp 7 hôm nay, các em sẽ tiếp tục luyện tập về Lũy thừa, nhưng với một tập hợp số khác: Lũy thừa của số hữu tỉ. Bài giảng đươc biên soạn bởi đội ngũ giáo viên giỏi của iToan, hy vọng sẽ truyền tải được đến các em học sinh những kiến thức bổ ích, những bài tập hay và thú vị nhất!

Mục tiêu bài học

Định nghĩa luỹ thừa một số tự nhiên ( Luỹ thùa bậc n của một số hữu tỉ x , kí hiệu xn , là tích của n thừa số x ” n là một số tự nhiên lớn hơn 1 ” )
Các ví dụ về luỹ thừa một số tự nhiên áp dụng làm từng bước dễ dàng .
Tích và thương của hai luỹ thừa cùng cơ số và các ví dụ .

Kiến thức cần nắm Lũy thừa của số hữu tỉ

Lũy thừa với số mũ tự nhiên

Lũy thừa bận n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x (n là một số tự nhiên lớn hơn 1).

(n thừa số x, x∈Q, n∈N, n>1).

Khi viết số hữu tỉ x dưới dạng ab (a,b∈Z,b≠0) ta có:

Ví dụ 1: Tính: (−3/4)2;

Giải:

(−3/4)2 = 9/16

Tích và thương của hai lũy thừa cùng cơ số

(Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ).

(Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia).

Ví dụ 2: Tính: (−3)2.(−3)3

Giải:

(−3)2.(−3)3 = (−3)5 = −35

Lũy thừa của lũy thừa

(Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ).

Ví dụ 3: Tính: (2^2)^3

Giải:

(2^2)^3 = 2^6

Lũy thừa của một tích

(Lũy thừa của một tích bằng tích các lũy thừa).

Ví dụ 4: Tính: (1,53).8

Giải:

(1,53).8 = (1,53).23 = (1,5.2)3 = 33 = 27

Lũy thừa của một thương

(Lũy thừa của một thương bằng thương các lũy thừa).

Ví dụ 5: Tính: 15327

Giải:

15327 = (3.5)333=53=125

Video bài giảng dưới đây vừa ngắn gọn, vừa bổ ích, giúp các em nắm bài hiệu quả hơn!

>> Xem thêm: Lũy thừa số hữu tỉ ( tiếp theo)

Giải bài tập SGK Lũy thừa của một số hữu tỉ

Bài 34 trang 22 SGK Toán 7 Tập 1

Trong vở bài tập của bạn Dũng có bài làm sau:

a) ( $-5)^2 . (-5)^3 = (-5)^6;$

b) $(0,75)^3 : 0,75 = (0,75)^2;$

c) $(0,2)^10 : (0,2)^5 = (0,2)^2;$

d) $\left[\left(- \dfrac{1}{7}\right)^2\right]^4 = \left(- \dfrac{1}{7}\right)^6;$

e) $\dfrac{50^3}{125} = \dfrac{50^3}{5^3} = \left(\dfrac{50}{5}\right)^3 = 10^3 = 1000;$

f) $\dfrac{8^{10}}{4^8} = \left(\dfrac{8}{4}\right)^{10 - 8} = 2^2 .$

Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có).

Đáp án và hướng dẫn giải

Các câu sai là a, c, d, f

Các câu đúng là b, e

Sửa lại:

a) $(-5)^2 .(-5)^3 = (-5)^5$

c) $(0,2)^{10} : (0,2)^5 = (0,2)^5$

d) $\left[\left(- \dfrac{1}{7}\right)^2\right]^4 = \left(- \dfrac{1}{7}\right)^8;$

f) $\dfrac{8^{10}}{4^8} = \dfrac{(2.4)^{10}}{4^8} = \dfrac{2^{10}.4^{10}}{4^8} = 2^{10}.4^2 = 2^{10}.2^4 = 2^{14}$

Bài 35 trang 22 SGK Toán 7 Tập 1

Ta thừa nhận tính chất sau đây: Với $a \ne 0, a \ne \pm1$ , nếu $a^m = a^n$ thì m = n. Dựa vào tính chất này, hãy tìm các số tự nhiên m và n, biết:

a) $\left(\dfrac{1}{2}\right)^m = \dfrac{1}{32};$

b) $\dfrac{343}{125} = \left(\dfrac{7}{5}\right)^n$

Đáp án và hướng dẫn giải

a) $\left(\dfrac{1}{2}\right)^m = \dfrac{1}{32}$

$\Leftrightarrow \left(\dfrac{1}{2}\right)^m = \left(\dfrac{1}{2}\right)^5$

$\Rightarrow m = 5$

b) $\dfrac{343}{125} = \left(\dfrac{7}{5}\right)^n$

$\Leftrightarrow \left(\dfrac{7}{5}\right)^3 = \left(\dfrac{7}{5}\right)^n$

$\Rightarrow n = 3$

Bài 36 trang 22 SGK Toán 7 Tập 1

Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ :

a) 10⁸ . 2⁸

b) 10⁸ : 2⁸

c) 25⁴ . 2⁸

d) 15⁸ . 9⁴

e) 27² : 25³

Đáp án và hướng dẫn giải

a) 10⁸ . 2⁸ = (10.2)⁸ = 20⁸

b) 10⁸ : 2⁸ = (10:2)⁸ = 5⁸

c) 25⁴ . 2⁸ = 5⁸ . 2⁸= 10⁸

d) 15⁸ . 9⁴ = 15⁸ . 3⁸ = 45⁸

e) 27² : 25³ = (3³)² : (5²)³ = 3^3.2 : 5^2.3 = 3⁶ : 5⁶

Bài 37 trang 22 SGK Toán 7 Tập 1

Tính giá trị các biểu thức sau:

a) $\dfrac{4^2.4^3}{2^{10}}$

b) $\dfrac{(0,6)^5}{(0,2)^6};$

c) $\dfrac{2^7.9^3}{6^5.8^2}$

d) $\dfrac{6^3 + 3.6^2 + 3^3}{-13}$

Đáp án và hướng dẫn giải

a) $\dfrac{4^2.4^3}{2^{10}} = \dfrac{4^5}{2^{10}} =\dfrac{(2^2)^5}{2^{10}} = \dfrac{2^{10}}{2^{10}} =1$

b) $\dfrac{(0,6)^5}{(0,2)^6} = \dfrac{(3.0,2)^5}{(0,2).(0,2)^5} = \dfrac{3^{5}.(0,2)^5}{(0,2).(0,2)^5} = \dfrac{3^{5}}{(0,2)} = \dfrac{243}{(0,2)} = 1215$

c) $\dfrac{2^7.9^3}{6^5.8^2} = \dfrac{2^2.2^5.(3^2)^3}{(2.3)^5.(2^3)^2} = \dfrac{2^2.2^5.3^6}{2^5.3^5.2^6} = \dfrac{3}{2^4} = \dfrac{3}{16}$

d) $\dfrac{6^3 + 3.6^2 + 3^3}{-13}$

$= \dfrac{(2.3)^3 + 3.(2.3)^2 + 3^3}{-13}$

$= \dfrac{2^3.3^3 + 2^2.3^3 + 3^3}{-13}$

$= \dfrac{3^3(2^3 + 2^2 + 1)}{-13}$

$= \dfrac{27.13}{-13} = -27$

Bài 38 trang 22 SGK Toán 7 Tập 1

a) Viết các số 2²⁷ và 3¹⁸ dưới dạng các lũy thừa có số mũ là 9.

b) Trong hai số 2²⁷ và 3¹⁸ số nào lớn hơn.

Đáp án và hướng dẫn giải

a) Ta có 2²⁷ = (2³)⁹ = 8⁹

3¹⁸ = (3²)⁹ = 9⁹

b) Vì 8 < 9 nên 8⁹ < 9⁹ hay 2²⁷ < 3¹⁸

Bài 39 trang 23 SGK Toán 7 Tập 1

Cho x ∈ Q và x ≠ 0. Viết x¹⁰ dưới dạng:

a) Tích của hai lũy thừa trong đó có một thừa số là x⁷.

b) Lũy thừa của x².

c) Thương của hai lũy thừa trong đó số bị chia là x¹².

Đáp án và hướng dẫn giải

a) x¹⁰ = x³ . x⁷

b) x¹⁰ = (x²)⁵

c) x¹⁰ = x¹² : x²

Bài 40 trang 23 SGK Toán 7 Tập 1

Tính:

a) $\left(\dfrac{3}{7} + \dfrac{1}{2} \right)^2 ;$

b) $\left(\dfrac{3}{4} - \dfrac{5}{6} \right)^2 ;$

c) $\dfrac{5^4.20^4}{25^5.4^5} ;$

d) $\left(\dfrac{-10}{3} \right)^5 . \left(\dfrac{-6}{5} \right)^4$

Đáp án và hướng dẫn giải

a) $\left(\dfrac{3}{7} + \dfrac{1}{2} \right)^2 = \left(\dfrac{6 + 7}{14} \right)^2 = \left(\dfrac{13}{14} \right)^2 = \dfrac{169}{196}$

b) $\left(\dfrac{3}{4} - \dfrac{5}{6} \right)^2 = \left(\dfrac{9 - 10}{12} \right)^2 = \left(\dfrac{-1}{12} \right)^2 = \dfrac{1}{144}$

c) $\dfrac{5^4.20^4}{25^5.4^5} = \dfrac{5^4.(5.4)^4}{(5.5)^5.4^5} =\dfrac{5^4.5^4.4^4}{5^5.5^5.4^5} = \dfrac{1}{5.5.4} = \dfrac{1}{100}$

d) $\left(\dfrac{-10}{3} \right)^5 . \left(\dfrac{-6}{5} \right)^4 = \dfrac{(-2.5)^5}{3^5}.\dfrac{(2.3)^4}{5^4} = \dfrac{-2^5.5^5.2^4.3^4}{3^5.5^4} = \dfrac{-2^9.5}{3} = \dfrac{-2560}{3}$

Bài 41 trang 23 SGK Toán 7 Tập 1

Tính:

a) $\left(1 + \dfrac{2}{3} - \dfrac{1}{4}\right). \left( \dfrac{4}{5} - \dfrac{3}{4}\right)^2$

b) $2 : \left(\dfrac{1}{2} - \dfrac{2}{3}\right)^3$

Đáp án và hướng dẫn giải

a) $\left(1 + \dfrac{2}{3} - \dfrac{1}{4}\right). \left( \dfrac{4}{5} - \dfrac{3}{4}\right)^2$

$= \left(\dfrac{12 + 8 - 3}{12}\right). \left(\dfrac{16 - 15}{20}\right)^2$

$= \dfrac{17}{12}. \left(\dfrac{1}{20}\right)^2$

$= \dfrac{17}{4800}$

b) $2 : \left(\dfrac{1}{2} - \dfrac{2}{3}\right)^3$

$= 2 : \left(\dfrac{3 - 4}{6}\right)^3$

$= 2 : \left(-\dfrac{1}{6}\right)^3$

$= 2 : \dfrac{-1}{216}$

$= 2 . \dfrac{-216}{1} = -432$

Bài 42 trang 23 SGK Toán 7 Tập 1

Tìm số tự nhiên n, biết:

a) $\dfrac{16}{2^n} = 2;$

b) $\dfrac{(-3)^n}{81} = -27;$

c) $8^n : 2^n = 4.$

Đáp án và hướng dẫn giải

a) $\dfrac{16}{2^n} = 2 \Leftrightarrow 2^n.2 = 16 \Leftrightarrow 2^{n + 1} = 2^4 \Leftrightarrow n + 1 = 4 \Leftrightarrow n = 3$

b) $\dfrac{(-3)^n}{81} = -27 \Leftrightarrow (-3)^n = (-3)^3.3^4 \Leftrightarrow (-3)^n = (-3)^7 \Leftrightarrow n = 7$

c) $8^n : 2^n = 4 \Leftrightarrow \left(\dfrac{8}{2}\right)^n = 2^2 \Leftrightarrow 4^n = 2^2 \Leftrightarrow 2^{2n} = 2^2 \Leftrightarrow 2n = 2 \Leftrightarrow n = 1$

Bài 43 trang 23 SGK Toán 7 Tập 1

Đố: Biết rằng 1² + 2² + 3² + … + 10² = 385, đố em tính nhanh được tổng:

S = 2² + 4² + 6² + … + 20²

Đáp án và hướng dẫn giải

S = 2² + 4² + 6² + … + 20²

= (2.1)² + (2.2)² + (2.3)² … (2.10)²

= 2².1² + 2².2² + 2².3² + … + 2².10²

= 2² (1² + 2² + … + 10² )

= 4 . 385 = 1540

Bài tập tự luyện Lũy thừa của một số hữu tỉ

Phần câu hỏi

Câu 1: Tính (2/3)^3

A. 8/9

B. 8/27

C. 4/9

D. 4/27

Câu 2: Số x^12 ( với x≠0) không bằng số nào sau đây?

A. x^18:x^6

B. x^4⋅x^8

C. x^2⋅x^6

Câu 3: Tìm giá trị của n biết: 4^n+4^(n+1)=80

A. 1

B. 2

C. 3

D. 4

Câu 4: Cho (2x+1)^3=−8. Giá trị của x là:

A. -3

B. −3/2

C. 4/3

D. Không có giá trị nào

Câu 5: Số 2^33 viết dưới dạng lũy thừa với số mũ bằng 8 là:

A. 9^7

B. 8^11

C. 13^8

D. Một đáp án khác

Phần đáp án

1.B 2.C 3.B 4.B 5.B

Lời kết

Lũy thừa là một dạng toán yêu cầu cả tư duy logic và sự tính toán cẩn thận. Các em có thể sử dụng thêm máy tính bỏ túi để hỗ trợ, nhưng đừng lạm dụng quá nhé. Để làm thêm các bài tập từ cơ bản đến nâng cao, các em có thể làm trên nền tảng Toppy. Toppy luôn nỗ lực mang đến cho các em học sinh những trải nghiệm học tập tốt nhất, hiệu quả nhất, cam kết giúp học sinh tiến bộ và thêm yêu thích môn Toán.

>> Xem thêm bài giảng khác tại iToan:

Lũy thừa của số hữu tỉ – Bài tập & Lời giải SGK Toán 7

Mục tiêu bài học

Kiến thức cần nắm Lũy thừa của số hữu tỉ

Lũy thừa với số mũ tự nhiên

Tích và thương của hai lũy thừa cùng cơ số

Lũy thừa của lũy thừa

Lũy thừa của một tích

Lũy thừa của một thương

Giải bài tập SGK Lũy thừa của một số hữu tỉ

Bài 34 trang 22 SGK Toán 7 Tập 1

Bài 35 trang 22 SGK Toán 7 Tập 1

Bài 36 trang 22 SGK Toán 7 Tập 1

Bài 37 trang 22 SGK Toán 7 Tập 1

Bài 38 trang 22 SGK Toán 7 Tập 1

Bài 39 trang 23 SGK Toán 7 Tập 1

Bài 40 trang 23 SGK Toán 7 Tập 1

Bài 41 trang 23 SGK Toán 7 Tập 1

Bài 42 trang 23 SGK Toán 7 Tập 1

Bài 43 trang 23 SGK Toán 7 Tập 1

Bài tập tự luyện Lũy thừa của một số hữu tỉ

Phần câu hỏi

Phần đáp án

Lời kết

Minh Phương

Trả lời Hủy

Mục tiêu bài học

Kiến thức cần nắm Lũy thừa của số hữu tỉ

Lũy thừa với số mũ tự nhiên

Tích và thương của hai lũy thừa cùng cơ số

Lũy thừa của lũy thừa

Lũy thừa của một tích

Lũy thừa của một thương

Giải bài tập SGK Lũy thừa của một số hữu tỉ

Bài 34 trang 22 SGK Toán 7 Tập 1

Bài 35 trang 22 SGK Toán 7 Tập 1

Bài 36 trang 22 SGK Toán 7 Tập 1

Bài 37 trang 22 SGK Toán 7 Tập 1

Bài 38 trang 22 SGK Toán 7 Tập 1

Bài 39 trang 23 SGK Toán 7 Tập 1

Bài 40 trang 23 SGK Toán 7 Tập 1

Bài 41 trang 23 SGK Toán 7 Tập 1

Bài 42 trang 23 SGK Toán 7 Tập 1

Bài 43 trang 23 SGK Toán 7 Tập 1

Bài tập tự luyện Lũy thừa của một số hữu tỉ

Phần câu hỏi

Phần đáp án

Lời kết

Minh Phương

Giá trị tuyệt đối của số hữu tỉ- Cộng, trừ, nhân, chia số thập phân - Toán lớp 7

Đường tròn Toán lớp 6- Sách giáo khoa Cánh diều

Trả lời Hủy