Phân thức đại số – Những tính chất cần nằm lòng

Toán học là một trong các môn khoa học cơ bản. Toán được đưa vào chương trình giáo dục, giảng dạy ở các cấp học khác nhau. Trong chương trình Toán 8, các bạn học sinh sẽ được làm quen với kiến thức về phân thức đại số. Trong bài viết này, Itoan tổng hợp lý thuyết và bài tập về phân thức đại số. Cùng Itoan khám phá ngay sau đây:

Định nghĩa

Phân thức đại số hay phân thức là một biểu thức có dạng A/B. Trong đó:

• A, B là các đa thức
• Phân thức có nghĩa với điều kiện B phải khác 0.

Hai phân thức bằng nhau:

Với hai phân thức A/B và C/D (Điều kiện: B,D khác 0)

Ta nói: A/B = C/D nếu A.D = B.C

Tính chất cơ bản của phân thức lớp 8

Tính chất cơ bản của phân thức toán 8 mà các bạn học sinh nên nhớ:

• A/B = A.M/B.M với điều kiện M là một đa thức khác 0
• A/B = A:N/B:N với điều kiện N là một đa thức khác không, trong phép tính này N được coi là nhân tử chung của phân thức

Quy tắc đổi dấu:

• Nếu đổi dấu cả tử và mẫu của một phân thức ta sẽ được một phân thức mới bằng với phân thức đã cho: A/B = -A/-B
• Đổi dấu phân thức và tử số: A/B = -(-A)/B
• Đổi dấu phân thức và mẫu số: A/B = -(A)/-B
• Đổi dấu mẫu: A/-B = -(A)/B

Toán 8 tính chất cơ bản của phân thức được áp dụng với đa dạng các bài tập từ cơ bản đến nâng cao và vẫn còn sử dụng thường xuyên khi lên các lớp trên.

Dạng bài quy đồng mẫu thức

Bước 1: Tìm mẫu chung

• Phân tích phần hệ số thành thừa số nguyên tố và phần biến nhân tử
• Mẫu chung bao gồm: phận hệ số của các hệ số mẫu và phần biến là tích các nhân tử chung và riêng của mỗi phần tử lấy số mũ lớn nhất.

Bước 2: Tìm nhân tử phụ của mỗi phân thức bằng cách lấy mẫu chung chia cho từng mẫu đa phân tích thành phân tử ở bước 1.

Bước 3: Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Dạng bài rút gọn phân thức đại số

Đây là dạng bài đơn giản tuy nhiên cần khả năng phân tích tốt để có thể tìm ra cách giải nhanh nhất. Dạng bài rút gọn phân thức đại số chính là cách biến đổi những phân thức phức tạp thành những phân thức đơn giản hơn và bằng với phân thức đa cho.

Muốn rút gọn phân thức một cách nhanh chóng ta có thể làm như sau:

• Phân tích tử và mẫu thành nhân tử để có thể tìm được nhân tử chung.
• Chia cả tử và mẫu cho nhân tử chung để rút gọn biểu thức

Ví dụ: Rút gọn phân thức sau A = (x + 2x²)/( x² – x)

Bước 1: Phân tích tử và mẫu để tìm nhân tử chung

A = x(1 + 2x)/x(x – 1)

Vậy ta có nhân tử chung là x

Bước 2: Chia cả tử và mẫu cho nhân tử chung x

Vậy ta được phân thức rút gọn b = (1 + 2x)/(x – 1) bằng với phân thức A = (x + 2x)/(x² – x)

Dạng bài cộng trừ hai phân thức

Toán 8 phân thức đại số rất hay gặp dạng toán này, một số lưu ý như sau:

• Các tính chất của phép cộng và phép trừ các phân thức

Giao hoán: A/B + C/D = C/D + A/B

Kết hợp: (A/B + C/D) + E/F = A/B + (B/C + E/F)

Đổi dấu: -(A)/B = -A/B = A/-B  hay -(-A)/B = A/B

• Cộng trừ hai phân thức cùng mẫu

Quy tắc: Muốn cộng, trừ hai phân thức có cùng mẫu thức ta cộng, trừ tử số với nhau và giữ nguyên mẫu số của phân thức.

Ví dụ: A/B + C/B = (A + C)/B

D/E – F/E = (D -F)/E

• Cộng trừ hai phân thức khác mẫu

Quy tắc: Muốn cộng, trừ hai phân thức khác mẫu thức ta quy đồng mẫu thức của các phân thức rồi cộng, trừ các phân thức có cùng mẫu đã được tìm được trước đó.

Dạng bài nhân chia hai phân thức

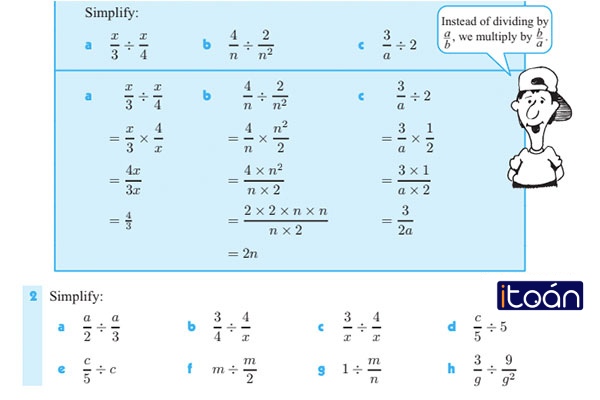
• Nhân hai phân thức

Quy tắc: Muốn nhân hai phân thức với nhau ta lấy tử nhân với từ và mẫu nhân với mẫu

Ví dụ: A/B * C/D = (A * C)/(B * D)

Giao hoán: A/B * C/D = C/D * A/B

Kết hợp: (A/B * C/D) * E/F = A/B * (C/D * E/F)

Phân phối đối với phép cộng: A/B * (C/D + E/F) = (A/B * C/D) + (A/B * E/F)

• Chia hai phân thức

Quy tắc: Muốn chia phân thức A/B cho phân thức C/D ( khác 0) ta chỉ cần lấy phân thức A?B nhân với nghịch đảo của phân thức C/D

Ví dụ: A/B : C/D = A/B * D/C

Phân thức nghịch đảo: Hai phân thức được gọi là nghịch đảo của nhau nếu tích của chúng bằng 1.

Ví dụ: Phân thức A/B và B/A là phân thức nghịch đảo của nhau

Dạng bài biến đổi các biểu thức hữu tỉ

Sử dụng các quy tắc cộng, trừ, nhân, chia phân thức để biến đổi các biến đổi các biểu thức hữu tỉ thành phân thức.

Lời kết

Trên đây là một số dạng bài đặc trưng của phân thức đại số lớp 8 mà Itoan muốn giới thiệu đến các bạn học sinh. Hy vọng giúp các bạn hiểu rõ hơn về dạng bài tập này. Nếu như bạn muốn học tốt môn toán thì đây sẽ là dạng bài tập mà bạn không nên bỏ qua.

Xem thêm: Cách chia đa thức một biến đã sắp xếp – Chinh phục Toán học