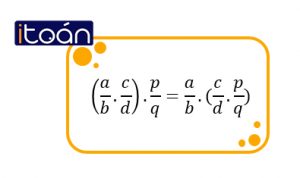Tính chất cơ bản của phép nhân phân số – Học tốt toán lớp 6

Bài học trước chúng ta đã có được cái nhìn tổng quan về phép tính nhân phân số phải không nào ? Cô mong rằng các bạn đều đã xem lại và ôn luyện lại bài cũ để có thể hiểu và nắm bắt thật tốt bài hôm nay nhé ! Bài học hôm nay sẽ giúp chúng ta hiểu về tính chất của phép nhân phân số , mang tên : “ Tính chất cơ bản của phép nhân phân số ” .Kính mời các bậc phụ huynh và quý thầy cô tham khảo .
Vào học ngay cùng Itoan các bạn nhé !
Mục tiêu bài học : Tính chất cơ bản của phép nhân phân số
Sau bài học này , các bạn cần nắm bắt được những nội dung kiến thức sau :
- Kiểm tra lại những kiến thức đã học tại bài học trước
- Nắm chắc được các nội dung liên qua đến tính chất cơ bản của phép nhân phân số
- Hoàn thành toàn bộ những bài tập được giao
Kiến thức cơ bản của bài học : Tính chất cơ bản của phép nhân phân số
Sau đây là phần tóm tắt nội dung cơ bản của bài học , yêu cầu các bạn nắm vững
Tương tự pháp nhân số nguyên, phép nhân phân số có các tính chất cơ bản sau:
-
-
-
- Tính chất giao hoán:
-
-
- Tính chất kết hợp:
- Nhân với số 1:
- Tính chất phân phối của phép nhân đối với phép cộng:
- Lũy thừa của một phân số: Với n∈N ta có:
Do tính chất giao hoán và kết hợp của phép nhân nên khi nhân nhiều số, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào sao cho việc tính toán được thuận tiện.
Hướng dẫn giải một số bài tập SGK Toán 6 bài : Tính chất cơ bản của phép nhân phân số
Khi đã cùng nhau điểm qua những nội dung lý thuyết cơ bản của bài học thì bây giờ , các bạn hãy làm một số bài tập sau đây nhé !
Bài 1 : ( trang 39 SKG Toán 6)
Trong hai câu sau đây, câu nào đúng?
Câu thứ nhất: Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu.
Câu thứ hai: Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu.
Lời giải:
Đáp án đúng cho câu hỏi trên là câu thứ hai.
Bài 2 :
Điền các số thích hợp vào bảng sau:
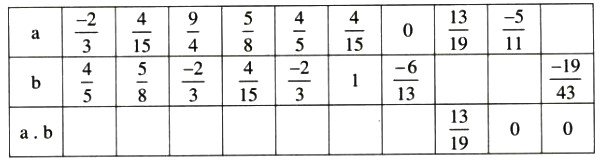
Lời giải:
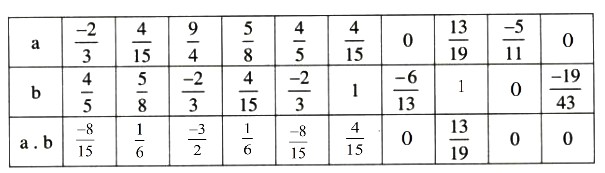
Bài 3 :
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể):

Lời giải:
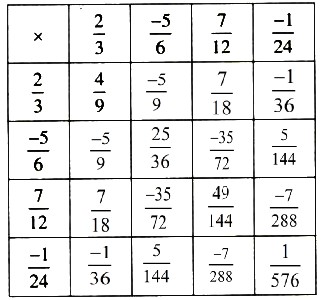
Bài 4 :
Tính giá trị các biểu thức sau:
Lời giải:
Bài 5 :
Tính giá trị các biểu thức sau:
với
với
với
Lời giải:
Tại thì
Tại thì
Tại thì
Bài 6 :Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Lời giải:
Bài 7 :
Tính:
| a) |
b) |
| c) |
d) |
Lời giải:
a)
b)
c)
d)
Bài 8 :
Tính diện tích và chu vi một khu đất hình chữ nhật có chiều dài km và chiều rộng
km.
Hướng dẫn:
Ta có một số những công thức cần tính toán như sau :
Chu vi hình chữ nhật bằng tổng chiều dài và chiều rộng nhân 2.
Diện tích hình chữ nhật bằng tích chiều dài với chiều rộng.
Lời giải:
Chu vi của khu đất là: km
Diện tích của khu đất là: km2
Bài 9:
| Toán vui: Một con ong và bạn Dũng cùng xuất phát từ A để đến B. Biết rằng mỗi giây ong bay được 5m và mỗi giờ Dũng đạp xe đi được 12km. Hỏi con ong hay bạn Dũng đến B trước?
|
 |
Hướng dẫn:
Để giải được các bài toán này , chúng ta cùng đi giải theo các bước sau đây :Tính vận tốc của con ong và bạn Dũng, sau đó so sánh vận tốc.
Vận tốc càng lớn thì thời gian đến B càng nhanh.
Lời giải:
Đổi 1 giờ = 3600 giây và 12km = 12000m
Vận tốc của con ong là: 5 : 1 = 5 (m/s)
Vận tốc của bạn Dũng là: 12000 : 3600 = (m/s)
Vì nên con ong đến B trước.
Bài 10:
Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A để đến B với vận tốc 15km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ B để đến A với vận tốc 12km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Lời giải:
Thời gian bạn Việt đi được tới chỗ gặp nhau là: 7 giờ 30 phút – 6 giờ 50 phút = 40 phút = giờ
Quãng đường bạn Việt đi được là: km
Thời gian bạn Nam đi được tới chỗ gặp nhau là: 7 giờ 30 phút – 7 giờ 10 phút = 20 phút = giờ.
Quãng đường bạn Nam đi được là: km
Quãng đường AB dài: 10 + 4 = 14km
Một số bài toán luyện tập thêm cho bài học : Tính chất cơ bản của phép nhân phân số
Bài 1 :
Tính – 5/7 . 2/11 + 5/7 . 9/11
A. 5/11 B. 19/4 C. 21/9 D. 23/11
Bài 2 :
Tính bằng cách hợp lí
−5/−10 x −268/91 + −5/−10 x 268/91
A. 0 B . -1 C. -2 D. 1
ĐÁP ÁN
- A 2. A
Lời kết :
Bài học sẽ trang bị thêm cho các bạn những kiến thức về phép nhân phân số . Đây đều là những kiến thức mới lạ đối với các bạn .Vì thế , các bạn cần tập trung học , ghi chép bài học đầy đủ cũng như hoàn thiện các bài tập được giao để đạt được hiểu quả tốt . Bài giảng trên được Itoan biên soạn rất kỹ lưỡng và chi tiết ,các bạn cần ôn luyện chăm chỉ để nhớ được những kiến thức đã học .Ngoài ra, các bạn có thể tham khảo thêm nhiều bài học khác tại :https://www.toppy.vn/
Chúc các bạn học tốt !
Xem thêm :
- Tính chất giao hoán của phép nhân – Bài giảng Toán 4
- Tính chất giao hoán của phép cộng – Bài tập & Lời giải Toán lớp 4
- Tính chất kết hợp của phép nhân – Bài tập & Lời giải Toán 4