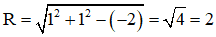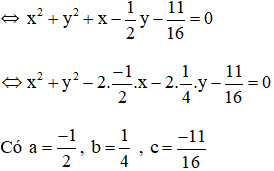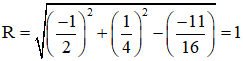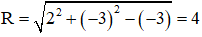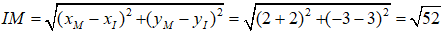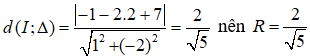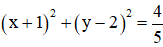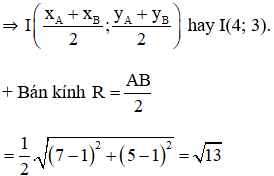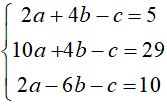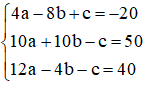Phương trình đường tròn – Bài tập Toán lớp 10

Tiết học hôm trước chúng ta đã được tìm hiểu và luyện tập về Phương trình đường thẳng, vậy Phương trình đường tròn thì viết như thế nào? Có tính chất nào khác? Cùng iToan học tập và đánh bay nỗi sợ môn Toán qua những bài giảng trực quan, thú vị nhé! Bài giảng: Phương trình đường tròn dược biên soạn bám sát theo chương trình sách giáo khoa Hình học lớp 10.

Nội dung kiến thức Phương trình đường tròn

Phương trình đường tròn có tâm và bán kính cho trước

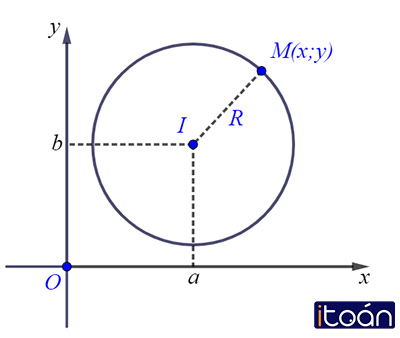
Trong mặt phẳng Oxy  , đường tròn (C)  tâm I(a,b)  bán kính R  có phương trình:

 (x−a)^2+(y−b)^2=R^2

Chú ý. Phương trình đường tròn có tâm là gốc tọa độ O  và bán kính R  là  x2+y2=R2

Ví dụ 1: Viết phương trình đường tròn nhận AB  làm đường kính với  A(1;1),B(7;5)

Giải

Gọi  I  là trung điểm của đoạn  AB suy ra I(4;3),AI=(4−1)2+(3−1)2−−−−−−−−−−−−−−−√=13−−√

Đường tròn cần tìm có đường kính là AB  suy ra nó nhận I(4; 3)  làm tâm và bán kính  R=AI=13−−√ nên có phương trình là  (x−4)2+(y−3)2=13 .

Nhận xét

Phương trình đường tròn (x−a)2+(y−b)2=R2  có thể viết dưới dạng

x2+y2−2ax−2by+c=0

trong đó  c=a2+b2−R2

●  Phương trình x2+y2−2ax−2by+c=0  là phương trình của đường tròn (C) khi  a2+b2−c>0.  Khi đó, đường tròn (C) có tâm I(a,b) bán kính

R=√a2+b2−c

Ví dụ

Trong các phương trình sau, phương trình nào biểu diễn đường tròn? Tìm tâm và bán kính nếu có.

a. x^2+y^2+2x−4y+9=0       (1)

b. x^2+y^2−6x+4y+13=0                (2)

c. 2x^2+2y^2−6x−4y−1=0            (3)

d.  2x^2+y^2+2x−3y+9=0                 (4)

Lời giải

a) Phương trình (1) có dang x^2+y^2−2ax−2by+c=0 với a=−1;b=2;c=9
Ta có a^2+b^2−c=1+4−9<0
Vây phương trình (1) không phải là phương trình đường tròn.
b) Ta có: a^2+b^2−c=9+4−13=0
Suy ra phương trình (2) không phải là phương trình đường tròn.
c) Ta có: (3)⇔x^2+y^2−3x−2y−12=0⇔(x−3/2)^2+(y−1)^2=15?4
Vây phương trình (3) là phương trình đường tròn tâm I(3/2;1)  bán kính R=15√2
d) Phương trình (4) không phải là phương trình đường tròn vì hê số của x^2 và y^2 khác nhau.

Phương trình tiếp tuyến của đường tròn

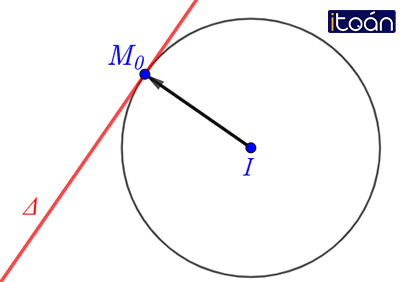
Cho đường tròn (C) có tâm I(a;b) và bán kính R.
Đường thẳng Δ là tiếp tuyến với (C) tại điểm M0(x0;y0).
Ta có:
M0(x0;y0)  thuộc Δ .
IM0−→−=(x0−a;y0−b)  là vectơ pháp tuyến của Δ

Do đó Δ có phương trình là

(x0−a)(x−x0)+(y0−b)(y−y0)=0

Ví dụ 3 : Viết phương trình tiếp tuyến tai điểm M(3;4) thuộc đường tròn

(C):(x−1)2+(y−2)2=8 .

Giải
(C) có tâm I(1;2), vây phương trình tiến tuyến với (C) tai điểm M(3;4) là:
(3−1)(x−3)+(4−2)(y−4)=0⇔2x+2y−14=0⇔x+y−7=0

Giải bài tập sách giáo khoa Phương trình đường tròn

Bài 1 (trang 83 SGK Hình học 10):

Tìm tâm và bán kính của các đường tròn sau:

a, x² + y²– 2x – 2y – 2 = 0

b, 16x² + 16y² + 16x – 8y -11 = 0

c, x² + y² – 4x + 6y – 3 = 0

Lời giải

Cách 1 : Xác định các hệ số a, b, c.

a) x² + y² – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2

⇒ tâm I (1; 1) và bán kính 

b) 16x² + 16y² + 16x – 8y –11 = 0

⇒ Đường tròn có tâm 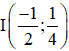 , bán kính 

c) x² + y² – 4x + 6y – 3 = 0

⇔ x² + y² – 2.2x – 2.(-3).y – 3 = 0

có hệ số a = 2, b = -3,c = -3

⇒ Đường tròn có tâm I(2 ; –3), bán kính 

Bài 2 (trang 83 SGK Hình học 10):

Lập phương trình đường tròn (C) trong các trường hợp sau:

a, (C) có tâm I(-2; 3) và đi qua M(2; -3);

b, (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng x – 2y +7 =0

c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).

Lời giải

a) (C) có tâm I và đi qua M nên bán kính R = IM

Ta có: 

Vậy đường tròn (C) : (x + 2)² + (y – 3)² = 52.

b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0

⇒ d(I; Δ) = R

Mà 

Vậy đường tròn (C) : 

c) (C) có đường kính AB nên (C) có :

+ tâm I là trung điểm của AB

Vậy đường tròn (C) : (x – 4)² + (y – 3)² = 13.

Bài 3 (trang 84 SGK Hình học 10):

Lập phương trình đường tròn đi qua ba điểm:

a, A(1; 2), B(5; 2), C(1; -3)

b, M(-2; 4), N(5; 5), P(6; -2)

Lời giải

Gọi phương trình đường tròn (C) là: x² + y² – 2ax – 2by + c = 0.

a) Do A(1; 2) ∈ (C) ⇔ 1² + 2² – 2.a.1 – 2.b.2 + c = 0

⇔ 5 – 2a – 4b + c = 0 ⇔ 2a + 4b – c = 5 (1)

Do B(5; 2) ∈ (C) ⇔ 5² + 2² – 2.a.5 – 2.b.2+ c = 0

⇔ 29 – 10a – 4b + c = 0 ⇔ 10a + 4b – c = 29 (2)

Do C(1; –3) ∈ (C) ⇔ 1² + (–3)² – 2.a.1 – 2.b.(–3) + c = 0

⇔ 10 – 2a + 6b + c = 0 ⇔ 2a – 6b – c = 10 (3)

Từ (1), (2) và (3) ta có hệ phương trình :

Giải hệ phương trình trên ta được nghiệm a = 3, b = –1/2, c = –1.

Vậy đường tròn đi qua ba điểm A, B, C là : x² + y² – 6x + y – 1 = 0.

b) M(–2 ; 4) ∈ (C) ⇔ (–2)² + 4² – 2.a.(–2) – 2.b.4 + c = 0 ⇔ 4a – 8b + c = –20 (1)

N(5; 5) ∈ (C) ⇔ 5² + 5² – 2.a.5 – 2.b.5 + c = 0 ⇔ 10a + 10b – c = 50 (2)

P(6; –2) ∈ (C) ⇔ 6² + (–2)² – 2.a.6 – 2.b.(–2) + c = 0 ⇔ 12a – 4b – c = 40 (3)

Từ (1), (2) và (3) ta có hệ phương trình:

Giải hệ phương trình trên ta được nghiệm a = 2, b = 1, c = –20.

Vậy đường tròn đi qua ba điểm M, N, P là : x² + y² – 4x – 2y – 20 = 0.

Bài 4 (trang 84 SGK Hình học 10):

Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và qua điểm M(2; 1).

Lời giải

Gọi đường tròn cần tìm là (C) có tâm I(a ; b) và bán kính bằng R.

(C) tiếp xúc với Ox ⇒ R = d(I ; Ox) = |b|

(C) tiếp xúc với Oy ⇒ R = d(I ; Oy) = |a|

⇒ |a| = |b|

⇒ a = b hoặc a = –b.

+ TH1: Xét a = b thì I(a; a), R = |a|

Ta có: M ∈ (C) ⇒ IM = R ⇒ IM² = R²

⇒ (2 – a)² + (1 – a)² = a²

⇔ 4- 4a + a² + 1 – 2a + a² = a²

⇔ 2a² – 6a + 5- a² =0

⇔ a² – 6a + 5 = 0

⇔ a = 1 hoặc a = 5.

* a = 1 ⇒ I(1; 1) và R = 1.

Ta có phương trình đường tròn (C): (x – 1)² + (y – 1)² = 1.

* a = 5 ⇒ I(5; 5), R = 5.

Ta có phương trình đường tròn (C) : (x – 5)² + (y – 5)² = 25.

+ TH2: Xét a = –b thì I(a; –a), R = |a|

Ta có: M ∈ (C) ⇒ IM = R ⇒ IM² = R²

⇒ (2 – a)² + (1 + a)² = a²

⇔ 4 – 4a + a² + 1+ 2a + a² – a² = 0

⇔ a² – 2a + 5 = 0 (Phương trình vô nghiệm)

Vậy có hai đường tròn thỏa mãn là: (C): (x – 1)² + (y – 1)² = 1 hoặc (C) : (x – 5)² + (y – 5)² = 25.

Bài 5 (trang 84 SGK Hình học 10):

Lập phương trình của đường tròn tiếp xúc với các trục tọa độ và có tâm nằm trên đường thẳng 4x – 2y – 8 = 0

Lời giải

Bài 6 (trang 84 SGK Hình học 10):

Cho đường tròn C có phương trình: x² + y² – 4x + 8y – 5 = 0

a, Tìm tọa độ tâm và bán kính của (C)

b, Viết phương trình tiếp tuyến với (C) đi qua điểm A(-1; 0)

c, Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng: 3x – 4y + 5 = 0.

Lời giải

a) x² + y² – 4x + 8y – 5 = 0

⇔ (x² – 4x + 4) + (y² + 8y + 16) = 25

⇔ (x – 2)² + (y + 4)² = 25.

Vậy (C) có tâm I(2 ; –4), bán kính R = 5.

b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:

(–1 – 2)² + (0 + 4)² = 3² + 4² = 5²= R²

⇒ A thuộc đường tròn (C)

⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A

⇒ (d’) là đường thẳng đi qua A và vuông góc với IA

⇒ (d’) nhận 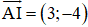 là một vtpt và đi qua A(–1; 0)

⇒ phương trình (d’): 3(x + 1) – 4(y – 0)= 0 hay 3x – 4y + 3 = 0.

2 phần vừa rồi các em đã làm đúng chưa, cùng làm tiếp phần c nhé!

c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).

(d) có 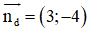 là một vtpt; 1 VTCP là u_d→(4; 3)

(Δ) ⊥ (d) ⇒ (Δ) nhận 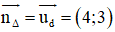 là một vtpt

⇒ (Δ): 4x + 3y + c = 0.

(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R

Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.

Bài tập tự luyện Phương trình đường tròn

Phần câu hỏi

Câu 1: Đường tròn tâm I(a,b) và bán kính R có dạng:

Câu 2: Điểu kiện để x2+y2−2ax−2by+c2=0 là một đường tròn là

Câu 3: Cho điểm M(x0;y0) thuộc đường tròn (C) tâm I(a,b) . Phương trình tiếp tuyến của đường tròn (C) tại điểm M là

Câu 4: Một đường tròn có tâm là điểm O(0,0) và tiếp xúc với đường thẳng Δ:x+y−4√2=0 . Hỏi bán kính đường tròn đó bằng bao nhiêu ?

Câu 5: Tìm tọa độ tâm đường tròn đi qua 3 điểm A(0;4),B(2;4),C(4;0) .

Phần đáp án

Lời kết