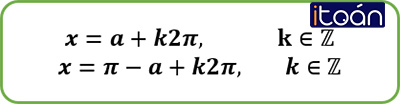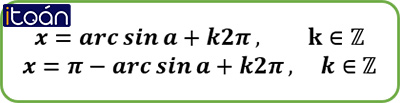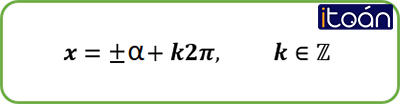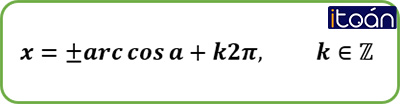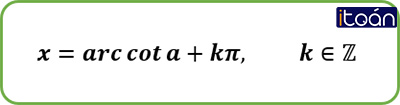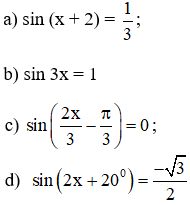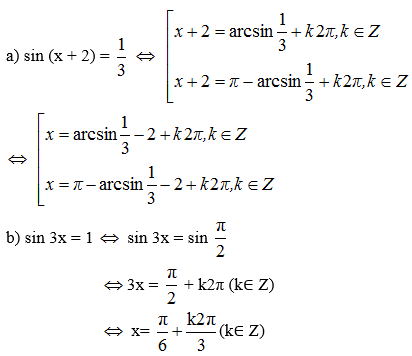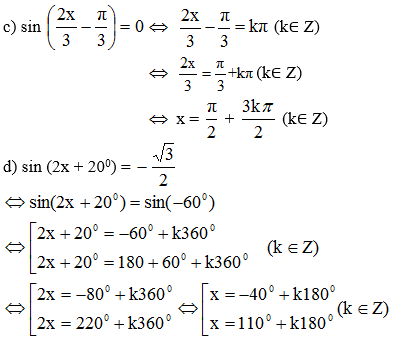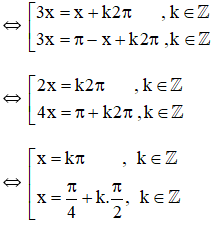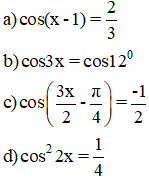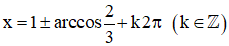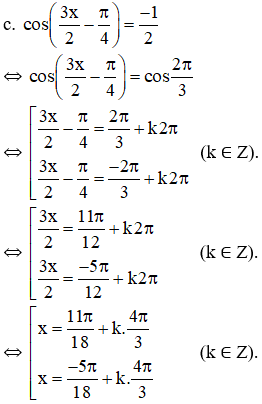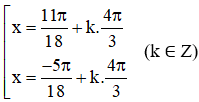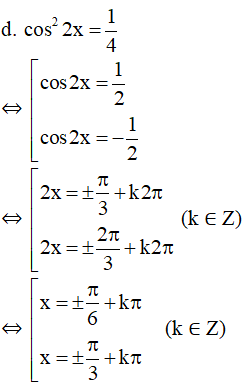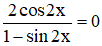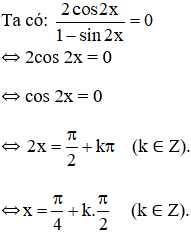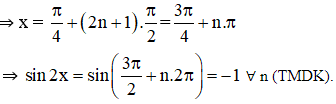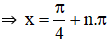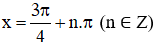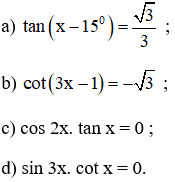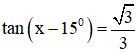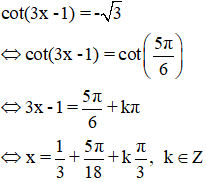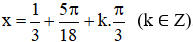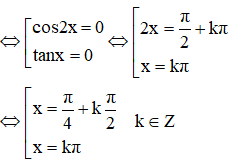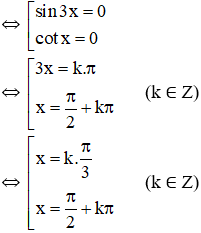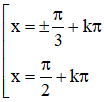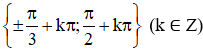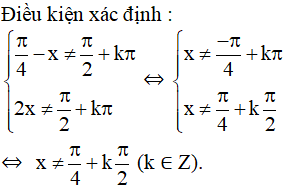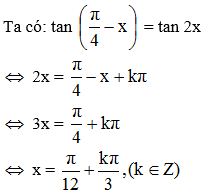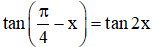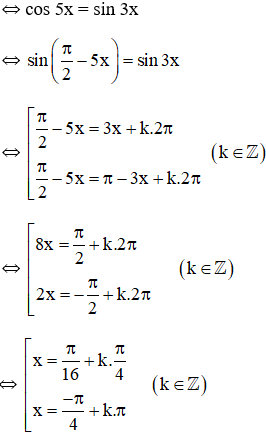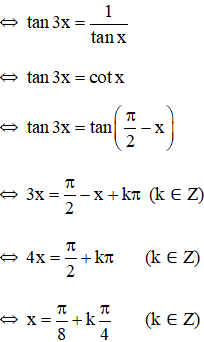Phương trình lượng giác cơ bản cần nhớ – Bài tập Đại số 10

Ở bài trước chúng ta đã được học về các hàm số lượng giác, bài hôm nay, chúng ta sẽ cùng tìm hiểu một số phương trình lương giác cơ bản cần ghi nhớ. Bài giảng: Phương trình lượng giác cơ bản – Đại số 10 được iToan biên soạn dựa theo bài học sách giáo khoa, với lý thuyết và giải bài tập chi tiết hơn, hy vọng sẽ giúp các em nắm được kiến thức cơ bản và thành thạo làm các bài tập liên quan.
Nội dung bài học Phương trình lượng giác cơ bản
Phương trình sin x= a
Xét phương trình sinx=a (1)
- Trường hợp |a|>1
Phương trình (1) vô nghiệm.
- Trường hợp |a|≤1
Gọi α (số đo radian) là một cung thỏa mãn sinα=a.
Nếu số thực α thỏa mãn điều kiện {−π2≤α≤π2sinα=a thì ta viết α=arcsina.
Khi đó các nghiệm của phương trình (1) là:
Chú ý
a. Phương trình sinx=sinα với α là một số cho trước, có các nghiệm là
x=α+k2π,k∈Z
x=π−α+k2π,k∈Z
Tổng quát
sinf(x)=sing(x)⇔[f(x)=g(x)+k2π,k∈Zf(x)=π−g(x)+k2π,k∈Z
b. Phương trình sinx=sinβ0 có các nghiệm là
x=β0+k3600,k∈Z
Và
x=1800−β0+k3600,k∈Z
c. Trong các công thức về nghiệm của phương trình lượng giác không dùng đồng thời hai đơn vị độ và radian.
d. Các trường hợp đặc biệt
sinx=0⇔x=kπ(k∈Z)
sinx=1⇔x=π2+k2π(k∈Z)
sinx=−1⇔x=−π2+k2π(k∈Z)
Phương trình cos x= a
Xét phương trình cosx=a (2)
- Trường hợp |a|>1
Phương trình (2) vô nghiệm.
- Trường hợp |a|≤1
Gọi α (radian) là một cung thỏa mãn cosα=a.
Khi đó phương trình (2) có các nghiệm là
Nếu số thực α thỏa mãn điều kiện {0≤α≤πcosα=a thì ta viết α=arccosa.
Khi đó các nghiệm của phương trình (1) là:
Chú ý
a. Phương trình cosx=cosα , với α là một số cho trước, có các nghiệm là
x=±α+k2π,k∈Z
Tổng quát
cosf(x)=cosg(x)⇔f(x)=±g(x)+k2π,k∈Z
b. Phương trình cosx=cosβ0 có các nghiệm là
x=±β0+k3600,k∈Z
c. Các trường hợp đặc biệt
cosx=0⇔x=π2+kπ(k∈Z)
cosx=1⇔x=k2π(k∈Z)
cosx=−1⇔x=π+k2π(k∈Z)
cosx=±1⇔cos2x=1⇔sin2x=0⇔sinx=0⇔x=kπ(k∈Z)
Phương trình tan x = a
Điều kiện của phương trình là x≠π2+kπ,(k∈Z)
Khi đó phương trình có nghiệm là
Chú ý
a. Phương trình tanx=tanα, với α là một số cho trước, có các nghiệm là:
x=α+kπ,k∈Z
Tổng quát
tanf(x)=tang(x)⇒f(x)=g(x)+kπ,k∈Z
b. Phương trình tan x=tanβ0có các nghiệm là
x=β0+k1800,k∈Z
c. Các trường hợp đặc biệt:
tanx=0⇔x=kπ(k∈Z)
tanx=±1⇔x=±π4+kπ(k∈Z)
Phương trình cot x=a
Điều kiện của phương trình là x≠kπ,(k∈Z)
Khi đó phương trình có nghiệm là
Chú ý
a. Phương trình cotx=cotα, với α là một số cho trước, có các nghiệm là:
x=α+kπ,k∈Z
Tổng quát
cotf(x)=cotg(x)⇒f(x)=g(x)+kπ,k∈Z
b. Phương trình cotx=cotβ0 có các nghiệm là:
x=β0+k1800,k∈Z
c. Các trường hợp đặc biệt:
cotx=0⇔x=π/2+kπ(k∈Z)
cotx=±1⇔x=±π/4+kπ(k∈Z)
Giải bài tập SGK trang 28 Phương trình lượng giác cơ bản
Bài 1 (trang 28 SGK Đại số 11): Giải các phương trình sau:
Lời giải:
Bài 2 (trang 28 SGK Đại số 11):
Với những giá trị nào của x thì giá trị của các hàm số y = sin 3x và y = sin x bằng nhau?
Lời giải:
Bài 3 (trang 28 SGK Đại số 11): Giải các phương trình sau:
Lời giải:
Vậy phương trình có họ nghiệm
b. cos 3x = cos 12º
⇔ 3x = ±12º + k.360º , k ∈ Z
⇔ x = ±4º + k.120º , k ∈ Z
Vậy phương trình có họ nghiệm x = ±4º + k.120º (k ∈ Z)
Vậy phương trình có hai họ nghiệm
Bài 4 (trang 29 SGK Đại số 11):
Giải phương trình
Lời giải:
+ Điều kiện: sin 2x ≠ 1.
+ Xét k lẻ. Đặt k = 2n + 1
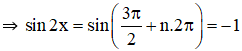
+ Xét k chẵn. Đặt k = 2n
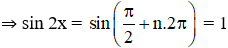
Vậy phương trình có họ nghiệm
Bài 5 (trang 29 SGK Đại số 11): Giải các phương trình sau:
Lời giải:
a. (Điều kiện : x – 15º ≠ 90º + k.180º với ∀ k ∈ Z)
⇔ x – 15º = 30º + k180º , k ∈ Z
⇔ x = 45º + k.180º, k ∈ Z
Vậy phương trình có họ nghiệm x = 45º + k.180º (k ∈ Z).
b. Điều kiện: 3x – 1 ≠ kπ ∀ k ∈ Z
Mọi giá trị thuộc họ nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có họ nghiệm
* Chú ý: Nếu các bạn sử dụng máy tính, kết quả cho được là 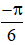
Các bạn sử dụng kết quả nào cũng đúng vì 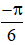
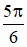
c. cos2x.tanx = 0
(Điều kiện xác định: 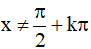
Vậy phương trình có hai họ nghiệm 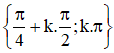
d. sin3x.cotx = 0
(Điều kiện xác định: x ≠ kπ ∀ k ∈ Z).
Kết hợp với điều kiện ta được
Vậy phương trình có các họ nghiệm
Bài 6 (trang 29 SGK Đại số 11):
Với giá trị nào của x thì giá trị của các hàm số y = tan(π/4 – x) và y = tan 2x bằng nhau?
Lời giải:
Kết hợp với điều kiện xác định suy ra 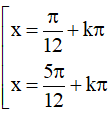
Vậy với 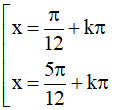
Bài 7 (trang 29 SGK Đại số 11): Giải các phương trình sau:
a. sin3x – cos5x = 0 ;
b. tan3x.tanx = 1
Lời giải:
a. sin3x – cos5x = 0
Vậy phương trình có hai họ nghiệm 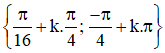
b. tan3x.tanx = 1 (Điều kiện: 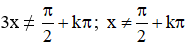
Các nghiệm thuộc họ nghiệm trên đều thỏa mãn điều kiện.
Vậy phương trình có họ nghiệm 
Bài tập tự luyện Phương trình lượng giác
Làm các bài tập tự luyện giúp em rèn luyện tư duy giải nhanh các bài trắc nghiệm:
Phần câu hỏi
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Phần đáp án
1.B 2.A 3. A 4.B 5.B
Lời kết
Sau bài học này, các em cần ghi nhớ các phương trình lượng giác cơ bản đã được giới thiệu bên trên và luyện tập các bài tập ứng dụng. Để giải quyết các thắc mắc và khó khăn trong các môn học, đặc biệt là môn Toán, các em có thể tìm kiếm Toppy. Các thầy cô Toppy luôn nỗ lực mang đến cho các em những bài giảng hay, dễ hiểu nhất, giúp các em tiến bộ hơn từng ngày.
Việc học không khó, hãy để Toppy lo !
>> Xem thêm: