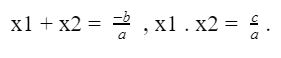Phương trình quy về phương trình bậc nhất bậc hai – Học cùng Itoan

Phương trình quy về phương trình bậc nhất bậc hai là phần kiến thức các em sẽ được học ở lớp 9. Đây là nội dung khá quan trọng để có thể làm các bài tập tiếp theo. Vậy nên, việc hệ thống lại là điều cực kỳ cần thiết. Cùng Itoan ôn lại các lý thuyết bài 7 phương trình quy về phương trình bậc hai và tìm hiểu về một số dạng bài tập có liên quan trong bài viết sau.
Phương trình bậc nhất
Cách giải và biện luận phương trình bậc nhất dạng ax + b = 0 (1) được thực hiện như sau:
a ≠ 0: (1) có nghiệm duy nhất
a = 0; b ≠ 0 (1) vô nghiệm.
a = 0; b = 0: (1) nghiệm đúng với mọi x∈R.
Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn.
Phương trình bậc hai
Phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) (2)
Δ = b2 − 4ac được gọi là biệt thức của phương trình (2).
+ Δ > 0 thì (2) có 2 nghiệm phân biệt
+ Δ = 0 thì (2) có nghiệm kép
+ Δ < 0 thì (2) vô nghiệm.
Định lí Vi–ét
Nếu phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 thì
Ngược lại, nếu hai số u và v có tổng u + v = S và tích u.v = P thì u và v là các nghiệm của phương trình x2 – Sx + P = 0.
Các dạng bài tập phương trình quy về phương trình bậc hai lớp 9
Các dạng bài tập về phương trình quy về phương trình bậc nhất bậc hai thường gặp như sau:
Phương trình trùng phương
Định nghĩa: Phương trình trùng phương là phương trình có dạng:
ax4 + bx2 + c = 0 (a ≠ 0)
Cách giải:
Giải phương trình trùng phương ax4 + bx2 + c = 0 (a ≠ 0)
+ Đặt x2 = t, t ≥ 0
+ Giải phương trình at2 + bt + c = 0
+ Với mỗi giá trị tìm được của t (thỏa mãn t ≥ 0), lại giải phương trình x2 = t.
Phương trình chứa ẩn ở mẫu thức
Phương trình quy về bậc nhất bậc hai chứa ẩn ở mẫu thức khi giải ta làm như sau:
Bước 1: Tìm điều kiện xác định của phương trình.
Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức.
Bước 3: Giải phương trình vừa nhận được.
Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho.

Phương trình chứa ẩn trong dấu giá trị tuyệt đối
Phương trình quy về phương trình bậc hai lớp 9 chứa ẩn trong dấu giá trị tuyệt đối cách giải là dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.
Ví dụ 1. Giải phương trình |x – 3| = 2x + 1. (3)
Cách giải:
Cách 1
a) Nếu x ≥ 3 thì phương trình (3) trở thành x – 3 = 2x + 1. Từ đó x = –4.
Giá trị x = –4 không thỏa mãn điều kiện x ≥ 3 nên bị loại.
b) Nếu x < 3 thì phương trình (3) trở thành –x + 3 = 2x + 1. Từ đó
Giá trị này thỏa mãn điều kiện x < 3 nên là nghiệm.
Kết luận. Vậy nghiệm của phương trình là x = 23
Cách 2.
Bình phương hai vế của phương trình (3) ta đưa tới phương trình hệ quả
(3) => (x – 3)2 = (2x + 1)2
=> x2 – 6x + 9 = 4x2 + 4x + 1
=> 3x2 + 10x – 8 = 0.
Phương trình cuối có hai nghiệm là x = –4 và
Thử lại ta thấy phương trình (3) chỉ có nghiệm là
Phương trình chứa ẩn dưới dấu căn
Để giải các phương trình quy về phương trình bậc nhất bậc hai có chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.
Ví dụ 2. Giải phương trình = x – 2 (4).
Cách giải
Điều kiện của phương trình (4) là
Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả
(4) => 2x – 3 = x2 – 4x + 4
=> x2 – 6x + 7 = 0.
Phương trình cuối có hai nghiệm là x = 3 + √2 và x = 3 – √2 . Cả hai giá trị này đều thỏa mãn điều kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x = 3 – √2 bị loại (vế trái dương còn vế phải âm), còn giá trị x= 3 + √2 là nghiệm (hai vế cùng bằng √2 + 1).
Kết luận. Vậy nghiệm của phương trình (4) là x= 3 + √2.
Giải phương trình quy về phương trình bậc hai chứa ẩn ở mẫu thức
Để giải phương trình quy về phương trình bậc hai chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn của phương trình.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình vừa nhận được ở bước 2.
Bước 4. So sánh các nghiệm tìm được ở bước 3 với điều kiện xác định và kết luận.
Phương trình đưa về dạng phương trình tích

Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng 0.
Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.
Giải phương trình bằng cách đặt ẩn phụ
Bước 1. Tìm điều kiện xác định (nếu có)
Bước 2. Đặt ẩn phụ và giải phương trình theo ẩn mới
Bước 3. Tìm nghiệm ban đầu và so sánh với điều kiện xác định ở bước 1 để kết luận nghiệm.
Giải phương trình chứa căn thức
Bước 1: Điều kiện xác định
Bước 2: Làm mất dấu căn bằng cách đặt ẩn phụ hoặc lũy thừa hai vế sau đó giải phương trình.
Bước 3: So sánh điều kiện và kết luận nghiệm.
Một số dạng khác
Ta có thể dùng hằng đẳng thức, thêm bớt hạng tử, hoặc đánh giá hai vế… để giải phương trình.
Các dạng bài tập phương trình quy về phương trình bậc hai rất đa dạng. Để các em có thể làm quen với các dạng bài tập này tốt hơn, hãy tìm hiểu thêm tại địa chỉ Itoan