Tổng hợp kiến thức về rút gọn phân thức – Chinh phục Toán 8

Toán học là một môn học quan trọng trong chương trình giáo dục các cấp. Trong chương trình Toán học 8, chúng ta sẽ đi tìm hiểu về phần kiến thức rút gọn phân thức. Rút gọn phân thức là gì? Các dạng bài tập liên quan, các lỗi thường gặp,… Cùng chúng tôi khám phá toán 8 rút gọn phân thức ngay sau đây nhé!
Tính chất cơ bản của phân thức
Tính chất cơ bản của phân thức toán 8:
- A/B = A.M/B.M. Trong đó: điều kiện M là một đa thức khác 0
- A/B = A:N/B:N. Trong đó điều kiện N là một đa thức khác không. N là nhân tử chung của phân thức.
Quy tắc đổi dấu mà học sinh nên nhớ:
- Đổi dấu phân thức và tử số: A/B = -(-A)/B
- Đổi dấu phân thức và mẫu số: A/B = -(A)/-B
- Đổi dấu mẫu: A/-B = -(A)/B
- Nếu đổi dấu tử và mẫu của một phân thức ta sẽ được một phân thức mới bằng với phân thức đã cho: A/B = -A/-B
Lý do cần làm các dạng bài tập rút gọn phân thức lớp 8
Rèn luyện tư duy logic
Rút gọn phân thức đại số lớp 8 là dạng bài tập đơn giản, không quá khó. Kiến thức này yêu cầu học sinh tập trung khi học và ứng dụng. Đây là dạng bài tập cơ bản giúp học sinh có thể hình dung và tư duy. Nhờ vậy, sau này có thể học tốt và làm được những dạng bài tập khó hơn, yêu cầu khả năng tư duy và phân tích vô cùng cao.
Tuy nhiên, rất nhiều bạn học sinh chủ quan cho rằng rút gọn các phân thức là những câu bài tập đơn giản. Vì vậy không tập trung vào việc học, phân tích cách giải mà chỉ làm qua loa để cho xong. Việc đó dẫn đến tính trạng kết quả học tập ngày càng sa sút. Như vậy, có thể thấy các dạng bài tập này chính là tiền đề để cho học sinh có thể phát triển tư duy và khả năng phân tích cho những dạng bài tập phân thức khó hơn.
Ứng dụng tốt hơn trong các môn học khác
Ngoài ra, cách rút gọn các phân thức không chỉ áp dụng cho riêng môn toán. Cách rút gọn này còn thường xuyên được sử dụng trong môn hóa học, môn lý, môn sinh học,… và các câu tính toán được áp dụng tại các trường đại học. Vì vậy, việc học tốt và làm tốt các dạng bài tập về việc làm gọn phân thức đại số sẽ giúp cho học sinh dễ dàng chinh phục những cột mốc quan trọng hơn trong tương lai.

Do đó, đây là dạng bài tập vô cùng quan trọng mà các bạn học sinh cần lưu ý để có phát triển con đường học vấn của bản thân. Và cách duy nhất để làm được điều đó là phải luôn tập trung cao độ khi giải những bài toán rút gọn để có thể tư duy và phát triển một cách nhanh chóng và toàn diện hơn.
Rút gọn phân thức đại số
Rút gọn phân thức là dạng bài cơ bản tuy nhiên muốn làm tốt thì học cần phải có khả năng phân tích bài toán nhanh nhạy. Dạng bài làm gọn các đại số chính là cách biến đổi những phân thức phức tạp thành những phân thức đơn giản hơn và bằng với phân thức đa cho.
Muốn thực hiện một cách nhanh chóng, chính xác ta có thể làm như sau:
- Phân tích tử và mẫu thành những nhân tử để có thể tìm được nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung để rút gọn biểu thức
Ví dụ: Rút gọn phân thức sau A = (x + 3x2)/( x2 – 2x)
Bước 1: Phân tích tử và mẫu để tìm nhân tử chung
A = x(1 + 3x)/x(x – 2)
Vậy ta có nhân tử chung là x
Bước 2: Chia cả tử và mẫu cho nhân tử chung x
Vậy ta được phân thức rút gọn b = (1 + 3x)/(x – 2) bằng với phân thức A = (x + 3x2)/( x2 – 2x)
Bài tập vận dụng
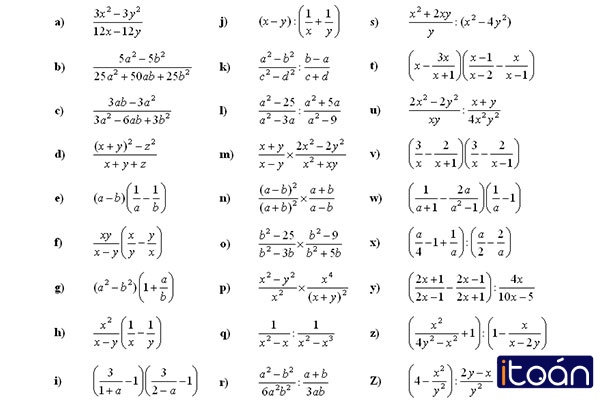
Bài 1: Rút gọn phân thức sau A = x(2y – 5) + xy +5x
Giải:
A = x(2y – 5) + xy +5x
= 2xy -5x +xy +5x
= 2xy + xy +5x – 5x
A = 3xy
Bài 2: Các nhận định dưới đây đúng hay sai?
- 3xy/9y = x/3
- (3xy + 3)/(9y + 3) = x/3
- (3xy + 3)/(9y + 3) = (x + 1)/6
- (3xy + 3)/(9y + 9) = x/3
Giải:
a) Đúng vì đã chia cả tử cả mẫu của vế trái cho 3y.
b) Vế phải chứng tỏ đã chia mẫu của vế trái cho 3y + 1 vì 9y + 3 = 3(3y + 1)
Nhưng tử của vế trái không có nhân tử 3y + 1. Nên phép rút gọn này sai.
c) Sai, vì y không phải là nhân tử chung của tử thức và mẫu thức của vế trái
d) Đúng, vì đã rút gọn phân thức ở vế trái với nhân tử chung là 3(y + 1)
Lời kết
Bài viết trên là một số kiến thức cơ bản mà về cách tính rút gọn phân thức đại số lớp 8 mà Itoan muốn gửi đến cho các bạn học sinh. Mong rằng, với những thông tin mà bài viết có thể giúp ích cho các bạn học sinh trong quá trình học tập.
