Số nguyên tố hợp số và bảng số nguyên tố – Để học tốt Đại số 6

Chào mừng các bạn đến với bài học của cô. Hôm nay cố sẽ dạy cho các em một phần kiến thức hoàn toàn mới lạ, đó là bài học Số nguyên tố hợp số và bảng số nguyên tố. Trong bài học này, cô đã phân chia rõ ràng các mục tiêu, lý thuyết và giải các bài tập trong sách giáo khoa nữa, hi vọng các bạn sẽ tiếp thu bài học thật tốt và đạt được kết quả cao trong học tập nha!
Mục tiêu của bài học Số nguyên tố hợp số và bảng số nguyên tố
Kiến thức bài học hôm nay có đôi chút liên quan đến những bài học trước, các bạn cố gắng học tốt những bài học trước và đặt ra mục tiêu cụ thể cho bài học hôm nay nhé!
- Bài toán về số nguyên tố , hợp số rút ra định nghĩa .
- Lập các số nguyên tố nhỏ hơn 100 và biết được số 0 và 1 không có trong bảng số nguyên tố .
- Các bài tập vận dụng giúp các con có kiến thức vững hơn .
Lý thuyết bài học Số nguyên tố hợp số và bảng số nguyên tố
Dưới đây là một số phần kiến thức quan trọng cơ bản cô đã biên soạn cho bài học hôm nay, các bạn nhớ học bài kỹ trước khi làm bài tập nhé!
1. Số nguyên tố. Hợp số.
- Số nguyên tố là số tự nhiên lớn hơn 1 , chỉ có hai ước là 1 và chính nó.
- Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.
Ví dụ
Trong các số 2,4,5,6 ta thấy:
– Số 2 và số 5 chỉ có hai ước là 1 và chính nó ⇒ chúng được gọi là số nguyên tố.
– Số 4 và số 6 có nhiều hơn hai ước ⇒ chúng được gọi là hợp số.
Lưu ý:
– Số 0 và số 1 không phải là số nguyên tố, cũng không là hợp số.
– Số 2 là số nguyên tố nhỏ nhất và là số nguyên tố chẵn duy nhất.
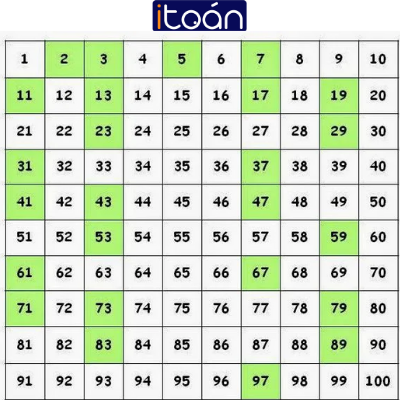
2. Lập bảng các số nguyên tố nhỏ hơn 100
Số nguyên tố là các số trong khung màu xanh
Nếu sau khi học xong phần lý thuyết phía trên mà các bạn vẫn chưa hình dung ra cách làm bài thì đừng vội bỏ cuộc nhé, các bạn có thể tham khảo thêm bài giảng của cô giáo Phạm Trần Thảo Vi đến từ trung tâm Toppy qua đoạn video dưới đây để hiểu bài học hơn nhé!
Xem thêm: Tập hợp các số nguyên – Hướng dẫn học tốt Đại số lớp 6 – itoan
Bài tập SGK Số nguyên tố hợp số và bảng số nguyên tố
Tiếp sau phần lý thuyết là phần giải các bài tập trong sách giáo khoa để áp dụng kiến thức vào bài tập nhé!
Bài 115 (trang 47 sgk Toán 6 Tập 1):
Các số sau là số nguyên tố hay hợp số? 312; 213; 435; 417; 3311; 67
Lời giải:
*Phương pháp kiểm tra một số a là số nguyên tố: Chia lần lượt a cho các số nguyên tố (2; 3; 5; 7; 11; 13; …) mà bình phương không vượt quá a
– 312 chia hết cho 2 nên không phải số nguyên tố.
– 213 có 2 + 1 + 3 = 6 nên chia hết cho 3. Do đó 213 không phải số nguyên tố.
– 435 chia hết cho 5 nên không phải số nguyên tố.
– 3311 chia hết cho 11 nên không phải số nguyên tố.
– 67 không chia hết cho 2; 3; 5; 7 nên 67 là số nguyên tố. (chỉ chia đến 7 vì các số nguyên tố khác lớn hơn 7 thì bình phương của chúng lớn hơn 67).
Bài 116 (trang 47 sgk Toán 6 Tập 1):
Gọi P là tập hơp các số nguyên tố. Điền kí hiệu ∈ , ∉ hoặc ⊂ vào ô trống cho đúng:
Lời giải:
Ta có:
83 không chia hết cho 2; 3; 5; 7 nên 83 là số nguyên tố. Do đó 83 ∈ P.
91 chia hết cho 7 nên 91 không phải số nguyên tố. Do đó 91 ∉ P.
15 là số tự nhiên nên 15 ∈ N.
Các số nguyên tố đều là số tự nhiên nên P ⊂ N.
Bài 117 (trang 47 sgk Toán 6 Tập 1):
Dùng bảng nguyên tố ở cuối sách tìm các số nguyên tố trong các số sau:
117; 131; 313; 469; 647
Lời giải:
Tra bảng số nguyên tố trang 128 SGK Toán 6 tập 1, ta được:
– Các số 131; 313; 647 là số nguyên tố.
Bài 118 (trang 47 sgk Toán 6 Tập 1):
Tổng (hiệu) sau là số nguyên tố hay hợp số?
a) 3.4.5 + 6.7 ; b) 7.9.11.13 – 2.3.4.7
c) 3.5.7 + 11.13.17 ; d) 16 354 + 67 541
Lời giải:
a) Ta có : (3.4.5) ⋮ 2 (vì 3.4.5 = 3.2.2.5 chia hết cho 2).
6.7 ⋮ 2 (vì 6.7 = 2.3.7 chia hết cho 2).
Do đó 3.4.5 + 6.7 ⋮ 2 nên 3.4.5 + 6.7 là hợp số.
b) 7.9.11.13 ⋮ 7 và 2.3.4.7 ⋮ 7 ⇒ (7.9.11.13 – 2.3.4.7) ⋮ 7.
Vậy (7.9.11.13 – 2.3.4.7) là hợp số.
c) 3.5.7 + 11.13.17 = 2536 ⋮ 2 nên 2536 là hợp số hay 3.5.7 + 11.13.17 là hợp số.
d) 16354 + 67541 = 83895 tận cùng bằng 5 nên chia hết cho 5. Do đó 16354 + 67541 là hợp số.
Bài 119 (trang 47 sgk Toán 6 Tập 1):
Thay chữ số vào dấu * để được hợp số: 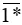
Lời giải:
Tra bảng các số nguyên tố ta có 11, 13, 17, 19, 31, 37 là các số nguyên tố.
– Các hợp số có dạng 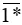
– Các hợp số có dạng 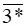
Bài tập tự luyện Số nguyên tố hợp số và bảng số nguyên tố
Phần bài tập tự luyện này cô biên soạn có kèm theo lời giải phía dưới, sau khi làm xong thì các bạn kiểm tra đáp án xem năng lực của mình như thế nào nhé!
Bài tập 1: Cho các số 21;71;77;101. Chọn phát biểu đúng trong các phát biểu sau?
A. Số 21 là hợp số, các số còn lại là số nguyên tố.
B. Có hai số nguyên tố và hai số là hợp số trong các số trên.
C. Chỉ có một số nguyên tố, còn lại là hợp số.
D. K
Bài tập 2: Trong các khẳng định sau, khẳng định nào sai?
A. Có hai số tự nhiên liên tiếp đều là số nguyên tố
B. Mọi số nguyên tố đều là số lẻ
C. Có ba số lẻ liên tiếp đều là số nguyên tố
D. Số 1 không là số nguyên tố và cũng không là hợp số
Bài tập 3: Có bao nhiêu số nguyên tố có hai chữ số mà chữ số hàng đơn vị là 7
A. 5
B. 6
C. 7
D. 8
Bài tập 4: Số tự nhiên có 2 chữ số khác nhau nhỏ nhất chia hết cho các số nguyên tố nhỏ hơn hoặc bằng 5 là:
A. 20
B. 25
C. 30
D. 35
Đáp án
Bài tập 1: B
Bài tập 2: B
Bài tập 3: A
Bài tập 4: C
Lời kết:
Vậy là bài giảng Số nguyên tố hợp số và bảng số nguyên tố của chúng ta sẽ khép lại tại đây, các bạn đã hiểu bài học chưa nhỉ? Cố gắng dành nhiều thời gian để tự ôn lại lý thuyết và làm bài tập nha! Ngoài bài học hôm nay, các bạn cũng có thể học tập nhiều bài học bổ ích khác nữa tại Toppy. Chúc các bạn học tập và áp dụng các kiến thức thật thành công.
Xem thêm bài giảng: