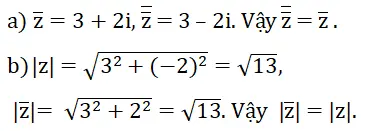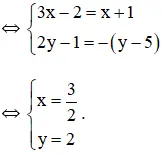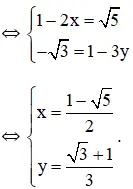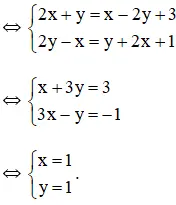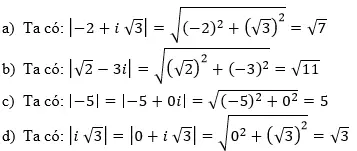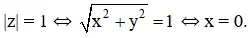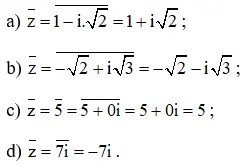Số phức – Chinh phục môn học giải tích lớp 12 cùng itoan

Số phức và các dạng toán liên quan đến số phức là một trong những nội dung mà nhiều bạn cảm thấy chúng khá trừu tượng và khó hiểu. Một phần nguyên nhân là chúng ta đã quá quen với số thực trong những năm học trước. Vì vậy ở bài viết này, itoan sẽ chọn lọc lý thuyết và giải các bài tập cơ bản trong sách giáo khoa giúp các bạn dễ dàng nắm được nội dung bài học Số phức nhé!
Mục tiêu bài học Số phức
Trước mỗi bài học, chúng ta đều đặt ra cho mình những mục tiêu nhất định để tạo động lực học bài!
- Hiểu được số phức, phần thực phần ảo của nó.
- Phân biệt được phần thực và phần ảo.
- Biết cách xác định được điều kiện để hai số phức bằng nhau.
Kiến thức Số phức
Lý thuyết của bài học hôm nay khá dễ hiểu, các bạn chú ý ghi chép lại bài học nhé!
1. Số i
Nghiệm của phương trình x2+1=0 được kí hiệu là i. Như vậy i2=−1
2. Định nghĩa số phức
Mỗi biểu thức dạng a+bi, trong đó a,b∈R, i2=−1 được gọi là một số phức.
Đối với số phức z=a+bi, ta nói a là phần thực, b là phần ảo.
Tập số phức kí hiệu là C .
Ví dụ 1: Xác định phần thực, phần ảo của các số phức sau: z=−5+4i,z=0−2i,z=7+0i
Giải
+ z=−5+4i, có phần thực bằng −5, phần ảo bằng 4.
+ z=0−2i, có phần thực bằng 0, phần ảo bằng −2.
+ z=7+0i, có phần thực bằng 7, phần ảo bằng 0.
3. Số phức bằng nhau
Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
a+bi=c+di ⇔ {a=c và b=d
Chú ý:
+ Mỗi số thực a được coi là số phức với phần ảo bằng 0, a=a+0i.
Như vậy, mỗi số thực cũng là một số phức.
+ Số phức 0+bi được gọi là số thuần ảo và viết đơn giản là bi.
bi=0+bi
i=0+1i
Số i được gọi là đơn vị ảo.
4. Biểu diễn hình học của các số phức
Điểm M(a;b) trong một hệ toạ độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z=a+bi
Ví dụ 3: Biểu diễn các số phức sau trên mặt phẳng toạ độ:
a)z=3+2i b)z=3−2i c)z=−3−2i
d)z=3i e)z=−3+2i h)z=4
Giải
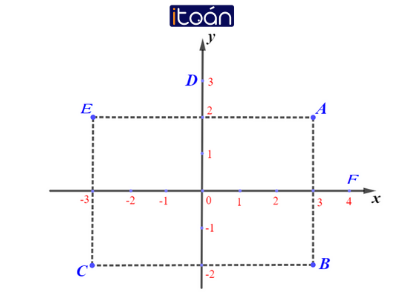
Gọi A,B,C,D,H lần lượt là điểm biểu diễn các số phức 3+2i, 3−2i, −3−2i, 3i, −3+2i, 4
Điểm A biểu diễn số phức z=3+2i .
Điểm B biểu diễn số phức z=3−2i .
Điểm C biểu diễn số phức z=−3−2i .
Điểm D biểu diễn số phức z=3i .
Điểm E biểu diễn số phức z=−3+2i .
Điểm H biểu diễn số phức z=4 .
5. Mô đun của số phức
Giả sử số phức z=a+bi được biểu diễn bởi điểm M(a;b) trên mặt phẳng tọa độ. Độ dài vectơ OM→ được gọi là môđun của số phức z và kí hiệu là |z|
6. Số phức liên hợp
Cho số phức z=a+bi. Ta gọi a−bi là số phức liên hợp của z và kí hiệu là z¯¯¯ =a−bi .
Ví dụ 4: Tìm số phức liên hợp của các số phức sau:
a)z=3+4i; b)z=2−5i;
c)z=1+3i ; d)z=−9i .
Giải
a) Số phức liên hợp của z=3+4i là z¯¯¯ =3−4i .
b) Số phức liên hợp của z=2−5i là z¯¯¯ =2+5i .
c) Số phức liên hợp của z=1+3i là z¯¯¯ =1−3i .
d) Số phức liên hợp của z=−9i là z¯¯¯ =9i .
Nếu học qua phần lý thuyết rồi mà vẫn còn nhiều khó khăn, các em có thể xem bài giảng của thầy giáo điển trai đến từ Toppy dưới đây nhé!
Giải bài tập SGK Số phức
Phần bài tập trong sách giáo khoa rất sát với lý thuyết chúng ta cần nhớ. Vậy nên các bạn chú ý giải hết rồi kiểm tra với đáp án của cô nhé!
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 130:
Tìm phần thực và phần ảo của các số phức sau: -3 + 5i, 4 – i√2, 0 + πi, 1 + 0i.
Lời giải:
| Số phức Phần thực Phần ảo | ||
| -3 + 5i | -3 | 5 |
| 4 – i√2 | 4 | -√2 |
| 0 + πi | 0 | π |
| 1 + 0i | 1 | 0 |
Số phức đó là z = 1/2 – √3/2 i.
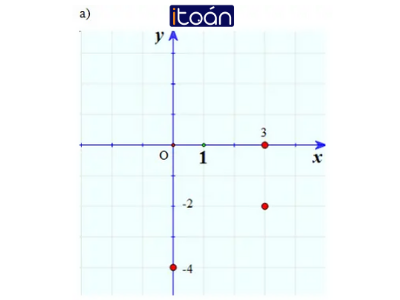
a) Biểu diễn trên mặt phẳng tọa độ các số phức sau: 3 – 2i, -4i, 3.
b) Các điểm biểu diễn số thực, số thuần ảo nằm ở đâu trên mặt phẳng tọa độ ?
b) Các điểm biểu diễn số thực nằm trên Ox, các điểm biểu diễn số ảo nằm trên Oy.
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 132:
Số phức nào có môđun bằng 0 ?
Lời giải:
Số phức là môđun bằng 0 là z = 0 + 0i.
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 132:
Biểu diễn các cặp số phức sau trên mặt phẳng tọa độ và nêu nhận xét:
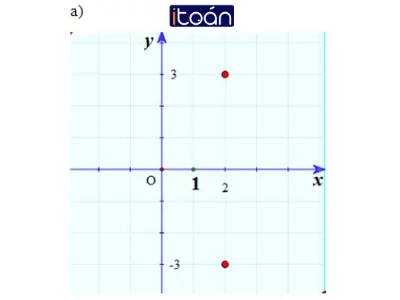
a) 2 + 3i và 2 – 3i;
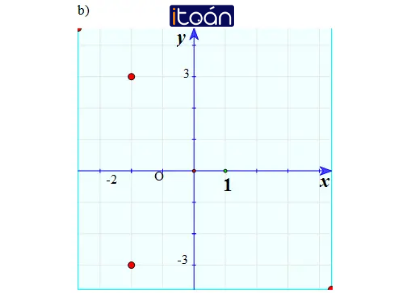
b) -2 + 3i và -2 – 3i.
Lời giải:
Hai điểm đối xứng nhau qua Ox.
Hai điểm đối xứng nhau qua Oy.
a) Hãy tính z– và 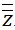
b) Tính |z| và |z–|. Nêu nhận xét.
Lời giải:
Bài 1 (trang 133 SGK Giải tích 12):
Tính phần thực phần ảo của số phức x, biết:
a) z = 1 – πi
b) z = √2 – i
c) z = 2 √2
d) z = -7i
Lời giải:
a) Phần thực: 1, phần ảo: -π
b) Phần thực: √2, phần ảo: -1
c) Phần thực: 2 √2, phần ảo: 0
d) Phần thực: 0, phần ảo: -7
Bài 2 (trang 133 SGK Giải tích 12):
Tìm các số thực x và y, biết:
a) (3x – 2) + (2y + 1)i = (x + 1) – (y – 5)i
b) (1 – 2x) – i√3 = √5 + (1 – 3y)i
c) (2x + y) + (2y – x)i = (x – 2y + 3) + (y + 2x + 1)i
Lời giải:
a) (3x – 2) + (2y – 1).i = (x + 1) – (y – 5).i
b) (1 – 2x) – i√3 = √5 + (1 – 3y)i
c) (2x + y) + (2y – x)i = (x – 2y + 3) + (y + 2x + 1)i
Bài 3 (trang 133 SGK Giải tích 12):
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bẳng -2
b) Phần ảo của z bẳng 3
c) Phần thực của z thuộc khoảng (-1;2)
d) Phần ảo của z thuộc đoạn [1;3]
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]
Lời giải:
a) Tập hợp các điểm thuộc đường thẳng x = -2
b) Tập hợp các điểm thuộc đường thẳng y = 3
c) Tập hợp các điểm thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x = 2 (hình có gạch sọc)
d) Phần mặt phẳng giới hạn bởi các đường thẳng song song y = 1 và y = 3( kể cả các điểm thuộc hai đường thẳng đó).
e) Các điểm thuộc hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y = -2, y = 2.
Bài 4 (trang 134 SGK Giải tích 12):
Tính |z|, với:
a) z = -2 + i √3
b) z = √2- 3i
c) z = -5
d) z = i√3
Lời giải:
Bài 5 (trang 134 SGK Giải tích 12):
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện:
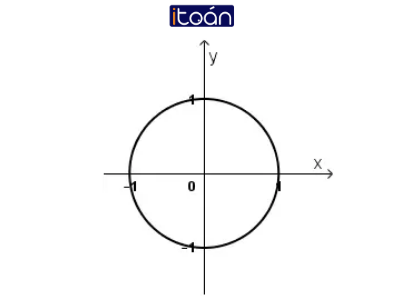
a) |z| = 1
b) |z| ≤ 1
c) 1<|z| ≤ 2
d) |z| = 1 và phần ảo của z = 1
Lời giải:
Gọi z = x + y.i có điểm biểu diễn là M(x; y).
a) |z| = 1 ⇔ √(x2 + y2 ) = 1 ⇔ x2 + y2 = 1
Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.
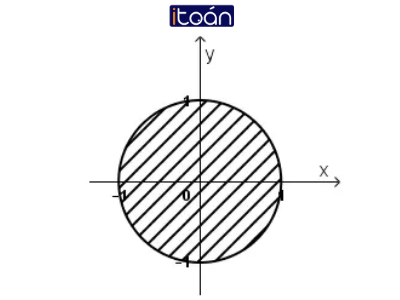
b) |z| ≤ 1 ⇔ √(x2 + y2 ) ≤ 1 ⇔ x2 + y2 ≤ 1
Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.
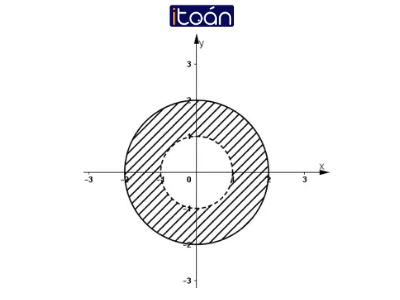
c) 1 < |z| ≤ 2 ⇔ 1 < √(x2 + y2 ) ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính tròn nhở bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.
d) Phần ảo của z bằng 1 ⇔ y = 1
Vậy điểm M(0; 1).
Bài 6 (trang 134 SGK Giải tích 12):
Tìm z, biết:
a) z = 1 – i√2
b) z = -√2 + i√3
c) z = 5
d) z = 7i
Lời giải:
Lời kết:
Vậy là bài học Số phức đã khép lại tại đây. Chúc mừng các em đã đạt được mục tiêu đề ra trong bài học. Để luyện tập nhiều hơn, các bạn hãy đến với Toppy . Ở đó có đầy đủ bài tập từ cơ bản đến nâng cao, giúp các bạn nắm vững bài học. Tạm biệt các em!
Xem thêm: