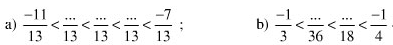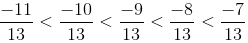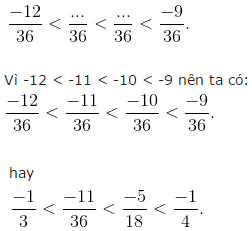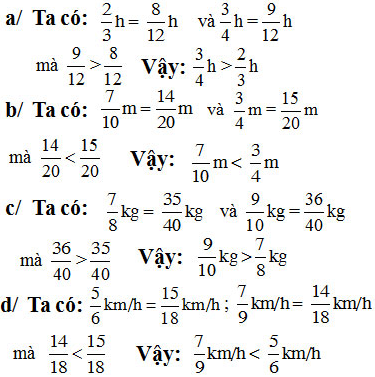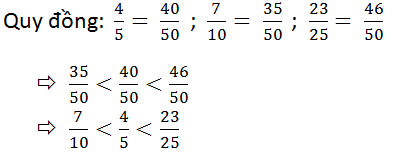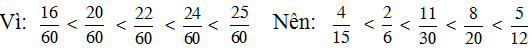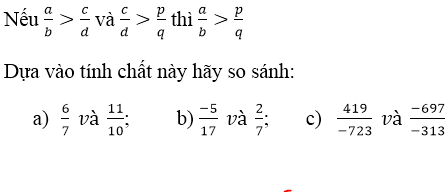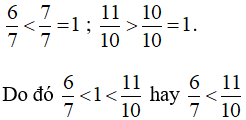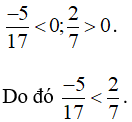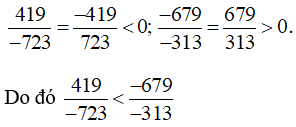So sánh phân số – Học tốt toán 6 cùng itoán

5/5 - (7 bình chọn)

Như chúng ta đã biết, phân số bao gồm có tử số và mẫu số, trong đó tử số là một số tự nhiên viết trên dấu gạch ngang, mẫu số là số tự nhiên khác 0 viết dưới dấu gạch ngang. Vậy làm thế nào để biết so sánh được nhiều phân số khác nhau? Hôm nay cô cùng các em sẽ cùng nhau tìm hiểu cách để So sánh phân số nhé. Cùng đến với bài học ngay thôi nào!

Mục tiêu bài học So sánh phân số

Nêu và vận dụng được quy tắc so sánh hai phân số cùng mẫu và không cùng mẫu
Nhận biết được phân số âm, dương.
Có kĩ năng viết các phân số đã cho dưới dạng các phân số cùng mẫu để so sánh phân số.

Để đạt được mục tiêu này, cô và các em cùng nhau đến với lý thuyết và bài tập để nắm rõ kiến thức bài học hôm nay nhé!

Lý thuyết So sánh phân số

1.1 So sánh hai phân số cùng mẫu:

So sánh 2 phân số cùng mẫu ta có quy tắc:

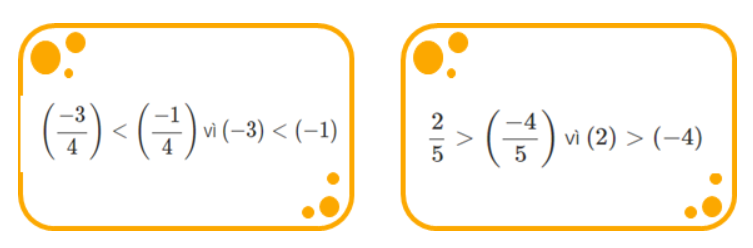
Trong hai phân số bất kì có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn

Ví dụ:

1.2 So sánh hai phân số không cùng mẫu:

So sánh 2 phân số không cùng mẫu ta có quy tắc:

Muốn so sánh 2 phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau.

Phân số nào có tử lớn hơn thì lớn hơn

Ví dụ: So sánh các phân số sau: $\frac{{10}}{{11}};\frac{{12}}{{13}}$ và $\frac{{15}}{{16}}$

Quy đồng tử số ta được $\frac{{10}}{{11}} = \frac{{60}}{{66}};\frac{{12}}{{13}} = \frac{{60}}{{65}};\frac{{15}}{{16}} = \frac{{60}}{{64}}$

Ta có $\frac{{60}}{{66}} < \frac{{60}}{{65}} < \frac{{60}}{{64}}$ nên $\frac{{10}}{{11}} < \frac{{12}}{{13}} < \frac{{15}}{{16}}$

*Lưu ý:

Phân số nào có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0. Phân số lớn hơn 0 được gọi là phân số dương.
Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0. Phân số nhỏ hơn 0 được gọi là phân số âm.

Các dạng toán thường gặp

Dạng 1: So sánh các phân số cùng mẫu số

– Bài toán 1. So sánh các phân số.

Bước 1: Viết phân số có mẫu âm thành phân số bằng nó và có mẫu dương.
Bước 2: So sánh các tử của các phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn

– Bài toán 2. Sắp xếp các phân số.

Bước 1. So sánh các phân số.
Bước 2. Sắp xếp các phân số theo thứ tự yêu cầu của bài toán.

Dạng 2: So sánh phân số khác mẫu số

– Cách 1: Quy đồng mẫu

Bước 1: Viết phân số có mẫu âm thành phân số bằng nó và có mẫu dương.
Bước 2: Quy đồng mẫu các phân số có mẫu dương
Bước 3: So sánh tử của các phân số đã quy đồng.

– Cách 2: Quy đồng tử

– Cách 3: Sử dụng phân số trung gian

Ngoài ra, chúng ta sẽ còn có các cách khác để so sánh (sẽ gặp trong ví dụ và bài tập) như rút gọn phân số hay sử dụng định nghĩa hai phân số bằng nhau.

Và để hiểu rõ hơn về các dạng toán này, chúng ta cùng nhau đến phần giải bài tập nhé!

Giải bài tập SGK So sánh phân số

Bài 37 (trang 23 SGK Toán 6 tập 2): Điền số thích hợp vào ô trống:

Lời giải:

a) Ta có -11 < -10 < -9 < -8 < -7, nên các số cần điền là:

b) Quy đồng mẫu số, ta đưa về dạng:

Bài 38 (trang 23-24 SGK Toán 6 tập 2):

Lời giải:

Gợi ý: quy đồng mẫu rồi so sánh.

Bài 39 (trang 24 SGK Toán 6 tập 2): Lớp 6B có 4/5 số học sinh thích bóng bàn, 7/10 số học sinh thích bóng chuyền, 23/25 số học sinh thích bóng đá. Môn bóng nào được nhiều bạn lớp 6B yêu thích nhất?

Lời giải:

Gợi ý: quy đồng mẫu rồi so sánh.

MSC = BSCNN(5, 10, 25) = 50. Thừa số phụ theo thứ tự là 10, 5, 2.

Vậy môn bóng đá được nhiều bạn lớp 6B thích nhất.

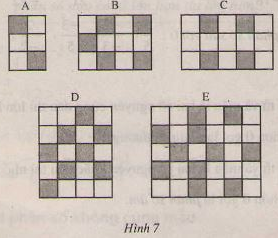
Bài 40 (trang 24 SGK Toán 6 tập 2): Lưới nào sẫm nhất?

a) Đối với mỗi lưới ô vuông ở hình 7, hãy lập một phân số có tử là số ô đen, mẫu là tổng số ô đen và trắng.

b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô đen so với tổng số ô là lớn nhất)

Lời giải:

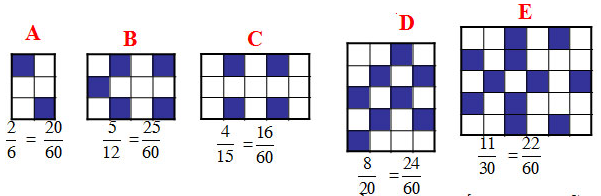
a) Lập phân số: tử số là số ô xanh, mẫu là tổng số ô xanh và trắng. Sau đó qui đồng:

b) Sắp xếp:

Vậy lưới sẫm nhất là lưới ở hình B.

Bài 41 (trang 24 SGK Toán 6 tập 2): Đối với phân số ta có tính chất:

Lời giải:

a) So sánh cả hai phân số với 1 ta có :

b) So sánh cả hai phân số với 0 ta có:

c) So sánh cả hai phân số với 0 ta có:

Bài tập tự luyện So sánh phân số

Câu 1: Sắp xếp các phân số $\frac{7}{{11}};\frac{3}{{11}};\frac{{ - 7}}{5};0;\frac{{ - 4}}{5};\frac{9}{{11}}$ theo thứ tự giảm dần ta được:

A. $\frac{{ - 7}}{5} > \frac{{ - 4}}{5} > \frac{7}{{11}} > 0 > \frac{9}{{11}} > \frac{3}{{11}}$

B. $\frac{7}{{11}} > \frac{{ - 4}}{5} > \frac{{ - 7}}{5} > \frac{3}{{11}} > \frac{9}{{11}} > 0$

C. $\frac{9}{{11}} > \frac{7}{{11}} > \frac{3}{{11}} > 0 > \frac{{ - 4}}{5} > \frac{{ - 7}}{5}$

D. $\frac{3}{{11}} > \frac{9}{{11}} > \frac{7}{{11}} > 0 > \frac{{ - 4}}{5} > \frac{{ - 7}}{5}$

Câu 2: Sắp xếp các phân số $\frac{{ - 3}}{4};\frac{1}{{12}};\frac{{ - 156}}{{149}}$ theo thứ tự tăng dần ta được:

A. $\frac{{ - 156}}{{149}} > \frac{{ - 3}}{4} > \frac{1}{{12}}$ B. $\frac{1}{{12}} < \frac{{ - 3}}{4} < \frac{{ - 156}}{{149}}$

C. $\frac{{ - 156}}{{149}} < \frac{{ - 3}}{4} < \frac{1}{{12}}$ D. $\frac{{ - 3}}{4} < \frac{{ - 156}}{{149}} < \frac{1}{{12}}$

Câu 3: So sánh các phân số $A = \frac{{3535.232323}}{{353535.2323}};B = \frac{{3535}}{{3534}};C = \frac{{2323}}{{2322}}$

A. A < B < C B. A = B < C C. A > B > C D. A = B = C

Câu 4: So sánh các phân số sau:

a, $\frac{{10}}{{11}};\frac{{12}}{{13}}$ và $\frac{{15}}{{16}}$

b, $\frac{{n + 1}}{{n + 5}}$ và $\frac{{n + 2}}{{n + 3}}$ (n là số tự nhiên)

Câu 5: So sánh hai phân số $A = \frac{{13579}}{{34567}}$ và $B = \frac{{13580}}{{34569}}$

Hướng dẫn giải bài tập tự luyện

Câu 1: C

Câu 2: C

Câu 3: A

Câu 4:

a, Quy đồng tử số ta được $\frac{{10}}{{11}} = \frac{{60}}{{66}};\frac{{12}}{{13}} = \frac{{60}}{{65}};\frac{{15}}{{16}} = \frac{{60}}{{64}}$

Ta có $\frac{{60}}{{66}} < \frac{{60}}{{65}} < \frac{{60}}{{64}}$ nên $\frac{{10}}{{11}} < \frac{{12}}{{13}} < \frac{{15}}{{16}}$

b, Để so sánh $\frac{{n + 1}}{{n + 5}}$ và $\frac{{n + 2}}{{n + 3}}$ , ta dùng phân số trung gian $\frac{{n + 1}}{{n + 3}}$

Ta có $\frac{{n + 1}}{{n + 5}} < \frac{{n + 1}}{{n + 3}}$ (so sánh hai phân số cùng tử) và $\frac{{n + 1}}{{n + 3}} < \frac{{n + 2}}{{n + 3}}$ (so sánh hai phân số cùng mẫu)

Vậy $\frac{{n + 1}}{{n + 5}} < \frac{{n + 2}}{{n + 3}}$

Câu 5:

Đặt 13579 = a và 34567 = b thì nhận thấy $A = \frac{a}{b}$ và $B = \frac{{a + 1}}{{b + 2}}$

$A = \frac{a}{b} = \frac{{a\left( {b + 2} \right)}}{{b\left( {b + 2} \right)}} = \frac{{ab + 2a}}{{b\left( {b + 2} \right)}};B = \frac{{a + 1}}{{a + 2}} = \frac{{b\left( {a + 1} \right)}}{{b\left( {b + 2} \right)}} = \frac{{ab + b}}{{b\left( {b + 2} \right)}}$

Ta thấy 13579.2 < 34567 tức là 2a < b

Suy ra A < B

Lời kết

Sau buổi học bài So sánh phân số, các em còn điều gì vướng mắc có thể comment dưới phần bình luận nhé, cô sẽ giải đáp cho các em. Ngoài ra, ở Toppy còn cung cấp khá nhiều bài học bổ ích khác nữa, các em có thể đăng nhập vào trang web làm bài luyện tập, củng cố và nâng cao kiến thức bài học. Chúc các em học tập tốt!

>> Xem thêm:

So sánh phân số – Học tốt toán 6 cùng itoán

Mục tiêu bài học So sánh phân số

Lý thuyết So sánh phân số

Các dạng toán thường gặp

Giải bài tập SGK So sánh phân số

Bài tập tự luyện So sánh phân số

Lời kết

Hoài Phương

Trả lời Hủy

Mục tiêu bài học So sánh phân số

Lý thuyết So sánh phân số

Các dạng toán thường gặp

Giải bài tập SGK So sánh phân số

Bài tập tự luyện So sánh phân số

Lời kết

Hoài Phương

Tam giác cân Toán 7 - Tổng hợp lý thuyết & Các dạng bài

Phép cộng phân số - Học tốt toán 6 cùng itoán

Trả lời Hủy