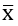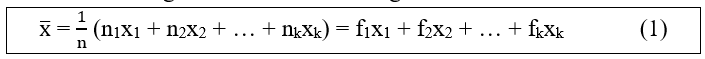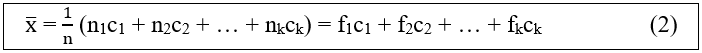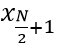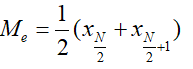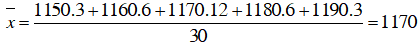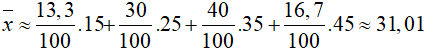Số trung bình cộng. số trung vị. mốt – Học toán lớp 10 đơn giản

Số trung bình cộng. số trung vị. mốt – Đây là bài học tiếp nối chuỗi những bài giảng về chủ đề tần số – tần suất. Đã được Itoan nhắc đến trong những bài đọc trước. Và đây là những chuyên đề mới, mở rộng hơn với nhiều phép toán từ đơn giản tới phức tạp. Yêu cầu kỹ năng đọc hiểu và phân tích đề bài, bên cạnh đó là tư duy nhanh. Hãy cùng Itoan rèn luyện ngay nhé!
Số trung bình cộng
Kí hiệu:
Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
| x1
x2 . xk |
n1
n2 . nk |
f1
f2 . fk |
| Cộng | n = n1 + … + nk | 100% |
Công thức
- Đối với bảng tần số
- Đối với bảng phân bố tần suất và tần số ghép lớp
Trong đó, ta có: ci, fi, ni là giá trị đại diện của lớp thứ i.

Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.
Số trung vị
Kí hiệu: Me
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa
Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là Me là :
+ Số đứng giữa dãy nếu số phần tử N lẻ: Me =
+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn:

Mốt
Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý
Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
Chọn đại diện cho các số liệu thống kê:
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
- Số các số liệu thống kê quá ít (n ≤ 10).
- Giữa các số liệu thống kê có sự chênh lệc quá lớn.
- Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)
Bài 1 (trang 122 SGK Đại Số 10): Tính số trung bình cộng của các bảng phân bố đã được lập ở các bài tập số 1 và số 2 của Bài 1.
Lời giải
Bài 1: Bảng phân bố tần số tuổi thọ của 30 bóng đèn điện.
| Tuổi thọ | Tần số |
| 1150 | 3 |
| 1160 | 6 |
| 1170 | 12 |
| 1180 | 6 |
| 1190 | 3 |
| Cộng | 30 |
Số trung bình:
Bài 2: Bảng phân bố tần suất ghép lớp độ dài của 60 lá dương sỉ trưởng thành:
| Lớp của độ dài (cm) | Tần suất | Giá trị đại diện |
| [10; 20) | 13,3 | 15 |
| [20; 30) | 30,0 | 25 |
| [30; 40) | 40,0 | 35 |
| [40; 50) | 16,7 | 45 |
| Cộng | 100 (%) |
Số trung bình:
Lời kết
Trên đây là bài viết nội dung về chủ đề Số trung bình cộng. số trung vị. mốt. Hy vọng đây sẽ là những kiến thức bổ ích dành cho các bạn học sinh. Đặc biệt là quý phụ huynh có nhu cầu ôn tập và giảng dạy cho các em. Trong quá trình học tập và ôn luyện, nếu có nhu cầu tìm kiếm đơn vị học tập uy tín, chất lượng. Hoặc muốn được giải đáp về những kiến thức liên quan đến môn học, hãy liên hệ với Itoan để được giải đáp nhanh nhất có thể