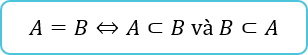Tổng hợp lý thuyết & bài tập về tập hợp – Đại số Toán 10

Tập hợp là phần kiến thức cơ bản trong chương trình toán 10 đại số. Các bạn học sinh cần nắm vững kiến thức lý thuyết và biết áp dụng vào bài tập. Trong bài viết này, Itoan tổng hợp lý thuyết và bài tập về tập hợp. Hãy cùng Itoan khám phá ngay thôi nào!
Lý thuyết về tập hợp
Tập hợp là một khái niệm cơ bản (không định nghĩa) của toán học.
Các tập hợp thường được kí hiệu bằng những chữ cái in hoa: A,B,...,X,Y. Các phần tử của tập hợp được kí hiệu bằng các chữ in thường a,b,...,x,y. Kí hiệu a∈A để chỉ a là một phần tử của tập hợp A hay a thuộc tập hợp A. Ngược lại a∉A để chỉ a không thuộc A.
Một tập hợp có thể được cho bằng cách liệt kê các phần tử của nó hoặc được cho bằng cách nêu tính chất đặc trưng của các phần tử của nó.
Ví dụ: A={1,2}
Hoặc A={x∈R/x2−3x+2=0}
Một tập hợp không có phần tử nào được gọi là tập hợp rỗng, kí hiệu Ø.
Biểu đồ ven
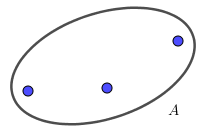
Để minh họa một tập hợp người ta dùng một đường cong khép kín giới hạn một phần mặt phẳng. Các điểm thuộc phần mặt phẳng này chỉ các phần tử của tập hợp ấy.
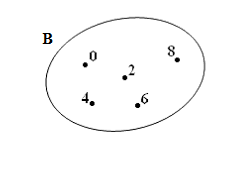
Ví dụ: B={0 ; 2 ; 4 ; 6 ; 8} được biểu diễn bằng biểu đồ Ven như sau:
Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B và viết A⊂B hoặc B⊃A.
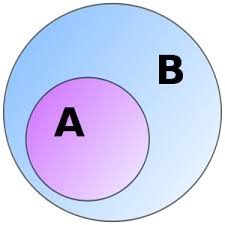
A⊂B⇔x∈A⇒x∈B
Nếu A không phải là một tập con của B ta viết A⊄B
Tính chất:
- A⊂A với mọi tập hợp A.
- A⊂B và B⊂C thì A⊂C.
- ∅⊂A với mọi tập hợp A.
Ví dụ: \(A={1;3;5;7;9},B={1;2;3;…;10}\)
Ta thấy mọi phần tử của A đều là phần tử của B, nên A⊂B.
Hai tập hợp bằng nhau
Hai tập hợp A và B bằng nhau, kí hiệu A=B, nếu mỗi phần tử của \(A\) là một phần tử của B và mỗi phần tử của B cũng là một phần tử của A.
Ví dụ:
C={x∈R∣2x2−5x+2=0}
D=12;2
Ta có
C={x∈R∣2x2−5x+2=0}={12;2}
⇒ C=D
Bài tập về tập hợp
Câu 1: Cho X={x∈R∣∣2x2−5x+3=0} , khẳng định nào sau đây đúng:
Câu 2: Cho tập hợp A={1,2,3,4,a,b} . Xét các mệnh đề sau đây:
(I) : “3∈A ”
(II) : “{3,4}∈A ”
(III) : “{a,3,b}∈A”
Trong các mệnh đề sau, mệnh đề nào đúng?
Câu 3:Hãy liệt kê các phần tử của tập hợp X={x∈R∣∣x2+x+1=0}
Câu 4: Cho A={x∈N|(2x−x2)(2x2−3x−2)=0};B={n∈N∗|3<n2<30}. Tìm A∩B
Câu 5: Cho tập hợp A={x∈R∣∣x4−6x2+8=0}. Tìm các phần tử của tập A.
Câu 6: Cho tập hợp A={ x∈N|x là ước chung của 36 và 120}. Tìm các phần tử của tập A.
Câu 7: Cho tập hợp A={x∈R∣∣(x2−1)(x2+2)=0}. Tìm các phần tử của tập A
Câu 8: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A={x∈R|4⩽x⩽9}
Bài tập nâng cao
Câu 9: Cho A={x∈R:x+2≥0},B={x∈R:5−x≥0}. Tìm A∖B.
Câu 10: Cho tập hợp A={x∈R∣∣x8−12x2+8=0}. Tìm các phần tử của tập A.
Trên là tổng của Toppy về lý thuyết và bài tập về tập hợp. Hy vọng những thông tin trên giúp ích cho các bạn học sinh trong học tập.