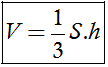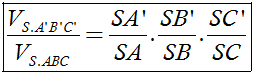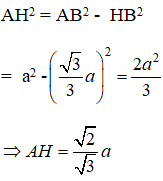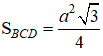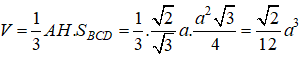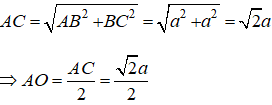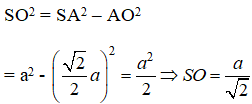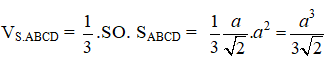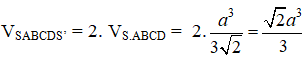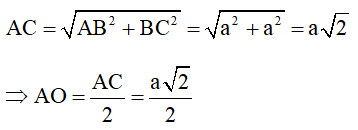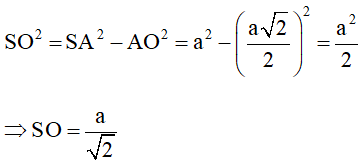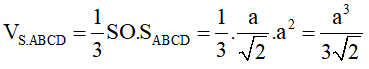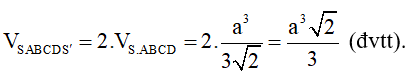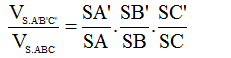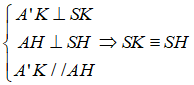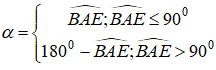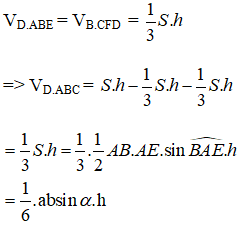Thể tích khối đa diện – Bài tập & Lời giải Toán 12

Khối đa diện là phần không gian được giới hạn nhờ một hình đa diện. Có nhiều loại khối đa diện cụ thể khác nhau, và mỗi loại lại có cách tính thể tích riêng. Trong bài giảng hôm nay: Thể tích khối đa diện, iToan sẽ đem đến cho các em kiến thức lý thuyết và hướng dẫn giải bài tập SGK chính xác & chi tiết nhất, giúp các em ôn tập tốt hơn!
Lý thuyết Thể tích khối đa diện
1. Hình lăng trụ đứng
Định nghĩa. Hình lăng trụ đứng là hình lăng trụ có cạnh bên tạo góc vuông với mặt đáy.
Tính chất. Mặt bên của hình lăng trụ đứng này là: các hình chữ nhật vuông góc với mặt đáy.
2. Hình lăng trụ đều
Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là hình đa giác đều.
Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.
3. Hình hộp đứng
Định nghĩa. Hình hộp đứng là hình hộp mà cạnh bên vuông góc với đáy.
Tính chất. Hình hộp đứng có 4 mặt xung quanh là 4 hình chữ nhật. 2 mặt đáy là 2 hình bình hành.
4. Hình hộp chữ nhật
Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là 2 hình chữ nhật.
Tính chất. Hình hộp chữ nhật có 6 mặt đều là 6 hình chữ nhật.
5. Hình lập phương
Định nghĩa. Hình lập phương là hình hộp chữ nhật mà 2 đáy và 4 mặt bên đều là hình vuông
Tính chất. Hình lập phương có 6 mặt đều là hình vuông.
6. Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.
Thể tích
1. Công thức tính thể tích khối chóp
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
2. Công thức tính thể tích khối lăng trụ
Trong đó: B là diện tích đáy, h là hiều cao khối lăng trụ
● Thể tích khối hộp chữ nhật: V = abc
Trong đó: a, b, c là ba kích thước của khối hộp chữ nhật.
● Thể tích khối lập phương: V = a3
Trong đó a là độ dài cạnh của hình lập phương.
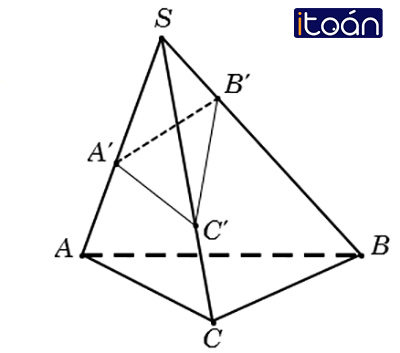
Tỉ số thể tích
Cho khối chóp S.ABC và A’, B’, C’ là các điểm tùy ý lần lượt thuộc SA, SB, SC ta có
Giải bài tập SGK 12 Thể tích khối đa diện
Bài 1: Tính thể tích khối tứ diện đều cạnh a.
Lời giải:
Gọi ABCD là tứ diện đều có cạnh a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)
Lại có: AB = AC = AD vì ABCD là tứ diện đều
⇒ HA là trục đường tròn ngoại tiếp tam giác BCD
⇒ HA ⊥ (BCD)
Vì tam giác BCD là tam giác đều nên H đồng thời trọng tâm tam giác BCD. Gọi M là trung điểm của CD.
Xét tam giác BCD ta có:
Áp dụng định lí pytago vào tam giác vuông AHB ta được:
Diện tích tam giác đều BCD cạnh a là:
Do đó, thể tích khối tứ diện đều ABCD là:
Bài 2: Tính thể tích khối bát diện đều cạnh a.
Lời giải:
Gọi khối bát diện đều là SABCDS’ cạnh a.
* Ta chia khối bát diện thành hai khối chóp tứ giác đều bằng nhau là:
S. ABCD và S’. ABCD có cạnh bằng a.
Khi đó, VSABCDS’ = VS.ABCD + VS’.ABCD = 2.VS.ABCD
Gọi O là giao điểm của AC và BD suy ra: SO ⊥ (ABCD)
* Ta tính thể tính khối tứ diện đều cạnh a.
Tứ giác ABCD là hình vuông cạnh a nên có diện tích là: SABCD = a2
Ta có:
Áp dụng định lí pytago vào tam giác SOA ta có:
Thể tích khối tứ diện đều S.ABCD là:
Thể tích khối bát diện đều cạnh a là:
Bài 3: Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số giữa thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Lời giải:
Gọi khối bát diện đều là SABCDS’ cạnh a.
* Ta chia khối bát diện thành hai khối chóp tứ giác đều bằng nhau là:
S.ABCD và S’.ABCD có cạnh bằng a.
Khi đó, VSABCDS’ = VS.ABCD + VS’.ABCD = 2.VS.ABCD
Gọi O là giao điểm của AC và BD suy ra: SO ⊥ (ABCD)
* Ta tính thể tính khối chóp tứ giác đều cạnh a.
Tứ giác ABCD là hình vuông cạnh a nên có diện tích là: SABCD = a2
Ta có:
Áp dụng định lí Pytago vào tam giác SOA ta có:
Thể tích khối chóp tứ giác đều S.ABCD là:
Thể tích khối bát diện đều cạnh a là:
Bài 4: Cho khối chóp S.ABC. Trên các đoạn thằng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng:
Lời giải:
Gọi H và K lần lượt là hình chiếu vuông góc của A và A’ trên mp(SBC),
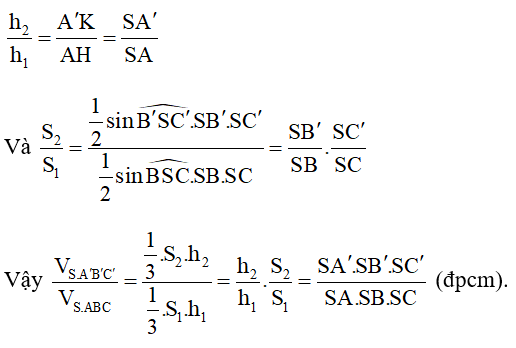
Đặt AH = h1 và A’K = h2 ,
S1 và S2 lần lượt là diện tích của hai tam giác SBC và SB’C’.
* Do A’K// AH nên bốn điểm A, A’; K và H đồng phẳng. (1)
Lại có, 3 điểm A, S, H đồng phẳng (2).
Từ (1) và (2) suy ra, 5 điểm A, A’, S. H và K đồng phẳng.
Trong mp(ASH) ta có:
⇒ Ba điểm S, H và K thẳng hàng.
* Ta có:
Bài 5: Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua C, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
Lời giải:
Bài 6: Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Lời giải:
Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
Do đó, thể tích khối tứ diện ABCD không đổi.
Lời kết
Bài giảng Thể tích khối đa diện kết thúc tại đây, để hiểu bài sâu và ghi nhớ lâu hơn,, các em nên làm thật nhiều các bài tập tự luyện, đặc biệt là các bài tập trắc nghiệm để luyện tư duy. Kho tài liệu bài giảng và bài tập từ cơ bản đến nâng cao được Toppy biên soạn và tổng hợp trên website.
Chúc các em học tốt!
>> Xem thêm:
- Tổng hợp công thức tính diện tích, thể tích hình lăng trụ đứng
- Tổng và hiệu hai Vecto
- Khối đa diện- Chinh phục hình học 12