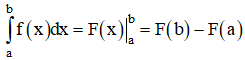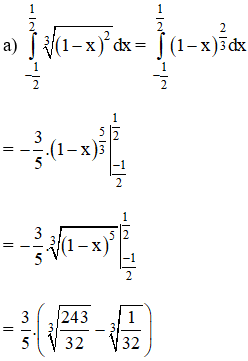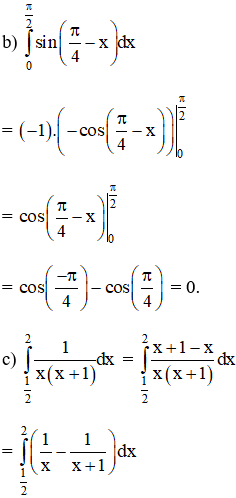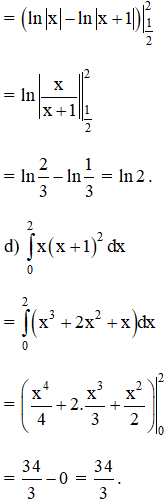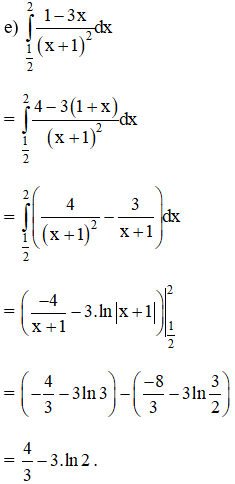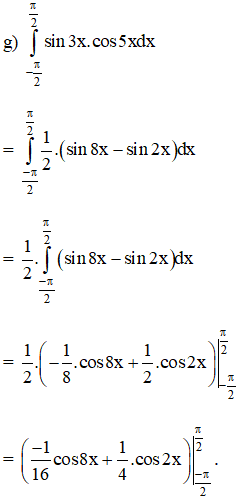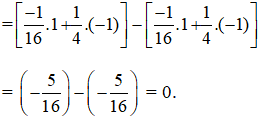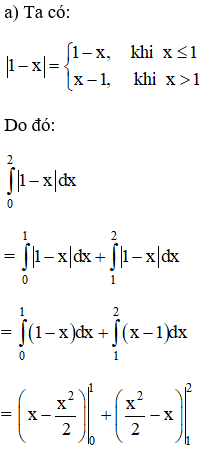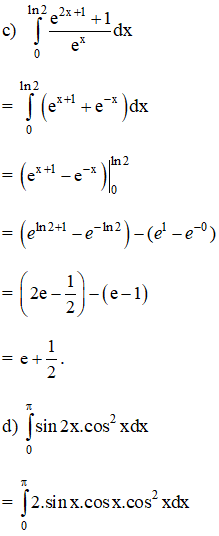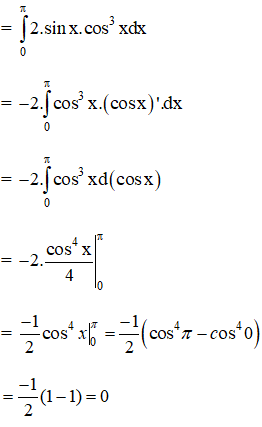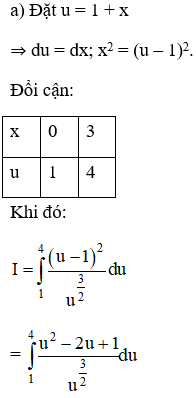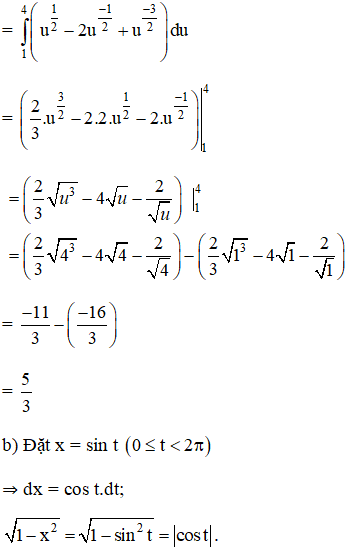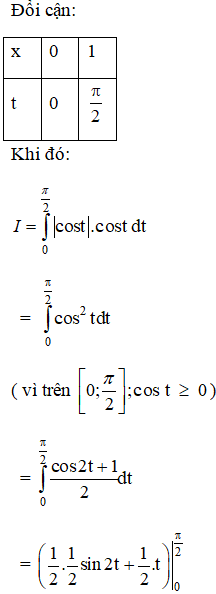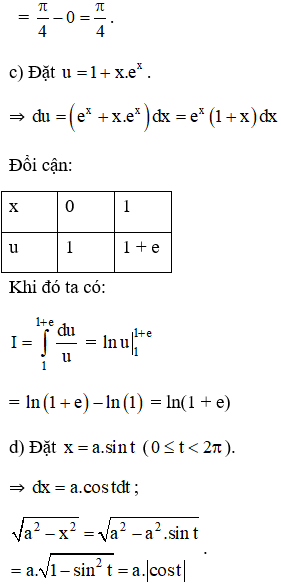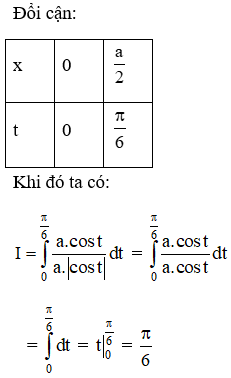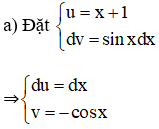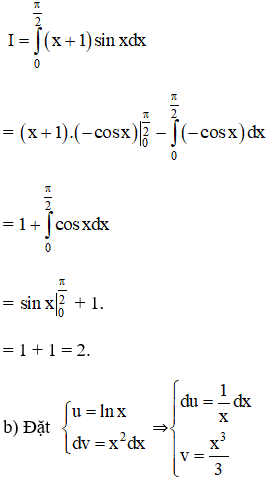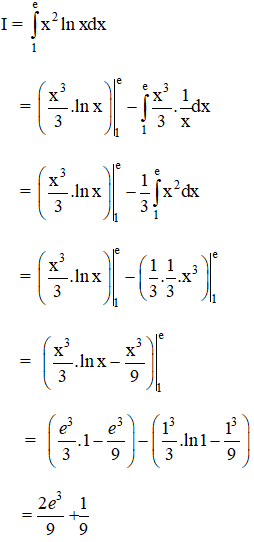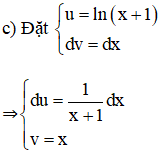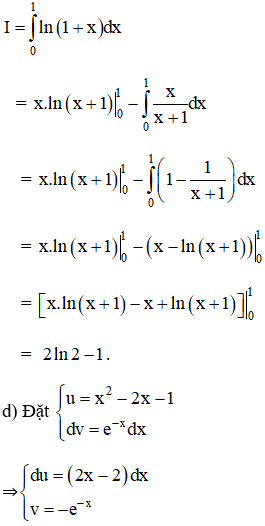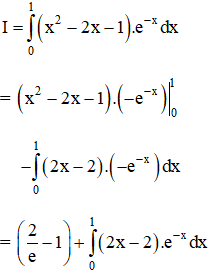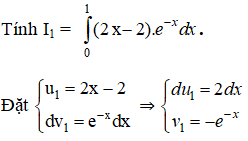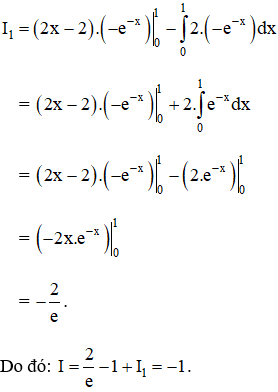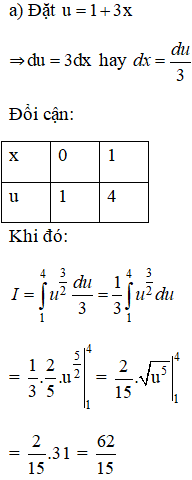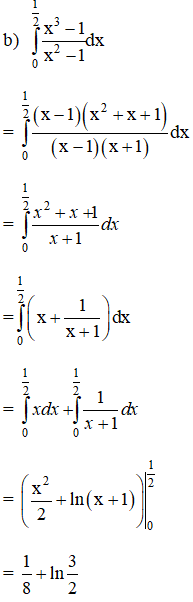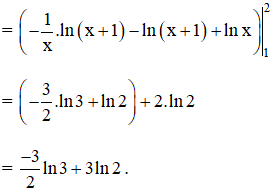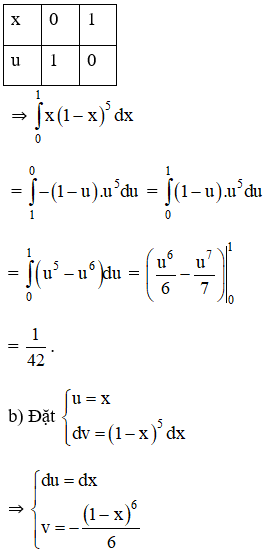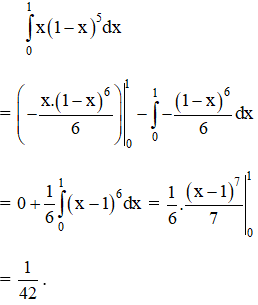Tích phân – Cùng itoan chinh phục SGK Giải tích lớp 12

Tích phân là một phần trong phân môn Giải tích lớp 12 và nó cũng thường có trong các đề thi tuyển sinh Đại học và Cao đẳng.Tích phân không phải đơn giản và nó thường gây lúng túng cho các bạn học sinh. Để góp phần giúp cho các bạn học sinh giảm bớt sự lúng túng khi “đụng độ” với tích phân, itoan xin giới thiệu bài giảng chi tiết hôm nay. Mời các bạn cùng tham khảo.
Mục tiêu của bài học tích phân
Kiến thức bài học hôm nay có đôi chút liên quan đến những bài học trước, các bạn cố gắng học tốt những bài học trước và đặt ra mục tiêu cụ thể cho bài học hôm nay nhé!
- Khái niệm, tính chất của tích phân.
- Các phương pháp tính tích phân (phương pháp đổi biến số, phương pháp tích phân từng phần)
- Áp dụng kiến thức đã học để giải bài tập liên quan tới hàm số.
Lý thuyết bài học tích phân
Dưới đây là một số phần kiến thức quan trọng cơ bản cô đã biên soạn cho bài học hôm nay, các bạn nhớ học bài kỹ trước khi làm bài tập nhé!
I. Khái niệm
1. Định nghĩa
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a;b].
Hiệu số F(b)−F(a) được gọi là tích phân từ a đến b của hàm số f(x) trên đoạn [a;b]. Kí hiệu: ∫abf(x)dx.
Vậy:
∫ab: dấu tích phân
a: cận dưới, b: cận trên.
2. Nhận xét
a) Tích phân của hàm số f từ a đến b có thể kí hiệu bởi ∫baf(x)dx hay ∫baf(t)dt. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến số. Tức là ∫baf(x)dx=∫baf(t)dt=∫baf(u)du
b) Ý nghĩa hình học: Nếu f(x) liên tục và không âm trên [a,b] thì diện tích của hình thang cong giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x=a,x=b là S=∫baf(x)dx
II. Tính chất
Tính chất 1:
∫ba k ⋅ f(x)dx = k ∫ba f(x)dx (k là hằng số )
Tính chất 2:
∫ba [f(x) ± g(x)] dx = ∫ba f(x)dx ± ∫ba g(x)dx
Tính chất 3:
∫ba f(x)dx = ∫ca f(x)dx + ∫bcf(x)dx (a<c<b)
III. Phương pháp tính tích phân
1. Phương pháp đổi biến số
a, Định lí
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số x=φ(t) có đạo hàm liên tục trên đoạn [α;β] sao cho φ(α)=a,φ(β)=b và a≤φ(t)≤b,∀t∈[α;β]. Khi đó
∫ba f(x)dx = ∫βαf(φ(t))φ′(t)dt
b. Phương pháp đổi biến số loại 1
Giả sử cần tính I=∫ab f(x)dx ta thực hiện các bước sau:
Bước 1: Đặt x=u(t) (với u(t) là hàm có đạo hàm liên tục trên [α;β], f(u(t)) xác định trên [α;β] và u(a)=a,u(β)=b) và a≥u(t)≥b.
Bước 2: Thay vào ta có: ∫ba f(x)dx=∫βαf(u(t))u′(t)dt .
Một số dạng thường dùng phương pháp đổi biến số dạng 1
Để tính tích phân I=∫ba f(x)dx, nếu f(x)=g[u(x)]⋅u′(x), ta có thể thực hiện phép đổi biến như sau
Bước 1: Đặt t=u(x)⇒dt=u′(x)dx.
Đồi cận x=a⇒t=u(a),x=b⇒t=u(b)
Bước 2: Thay vào ta có
2. Phương pháp tích phân từng phần
a, Định lí
Nếu u=u(x) và v=v(x) là hai hàm số có đạo hàm liên tục trên [a;b] thì:
∫ba u(x) v′(x) dx = (u(x) v(x))|ba−∫ba u′(x) v(x)dx
Hay
∫ba udv = uv|ba − ∫bavdu
Ta thường gặp các dạng sau
Sẽ dễ dàng hơn khi tiếp thu kiến thức mới nếu bạn kết học học lý thuyết và nghe giảng qua video dưới đây!
Hướng dẫn giải bài tập SGK: tích phân
Để nắm chắc lý thuyết, cô và các bạn cùng nhau giải các bài tập trong sách giáo khoa nhé!
Bài 1 (trang 112)
Tính:
Kiến thức áp dụng
+ Tích phân từ a đến b của hàm số f(x) có nguyên hàm là F(x) là:
+ Một số nguyên hàm sử dụng:
Hướng dẫn giải
Bài 2 (trang 112)
Tính:
Hướng dẫn giải:
Bài 3 (trang 113)
Sử dụng phương pháp đổi biến, hãy tính:
Hướng dẫn giải:
Bài 4 (trang 113)
Sử dụng phương pháp tích phân từng phần, hãy tính:
Hướng dẫn giải:
Theo công thức tích phân từng phần ta có:
Theo công thức tích phân từng phần ta có:
Theo công thức tích phân từng phần:
Theo công thức tích phân từng phần:
Theo công thức tích phân từng phần:
Bài 5 (trang 113)
Tính:
Hướng dẫn giải:
Bài 6 (trang 113)
Tính 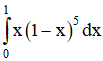
a) Đổi biến số u = 1 – x;
b) Tính tích phân từng phần.
Hướng dẫn giải:
a) Đặt u = 1 – x;
⇒ du = -dx
Đổi biến :
Theo công thức:
Lời kết:
Ứng dụng Tích phân là một dạng toán hay và đòi hỏi tính vận dụng cao. Các bạn nên dành nhiều thời gian để luyện bài tập và các chuyên đề liên quan để đạt kết quả tốt nhất! Các bạn có thể tham khảo thêm nhiều bài học thú vị và bổ ích khác tại Toppy. Toppy sẽ giúp các em học tốt và tìm được niềm đam mê với môn học yêu thích! Chúc các bạn học tập thật tốt! Chúng ta sẽ gặp lại nhau trong những bài học tiếp theo nhé!
Xem thêm các bài viết có liên quan: