Tính chất hình chóp đều – Chinh phục Hình học Toán 8

Hình chóp là loại hình học không gian khó và khá phức tạp. Tuy nhiên trong chương trình Toán 8, hình chóp đều là một trong những kiến thức trọng tâm quan trọng. Chính vì vậy để hiểu rõ tính chất hình chóp đều, diện tích xung quanh của hình chóp đều và các dạng bài tập thường gặp, hãy cùng Itoan tìm hiểu qua bài giảng chi tiết sau đây:
1. Khái niệm hình chóp đều
Hình chóp đều là hình có các đáy là đa giác đều như hình tam giác đều, hình vuông,… và tâm của đáy hình chóp trùng với chân đường cao thì đó được gọi là hình chóp đều. Để hiểu rõ hơn về hình chóp này, hãy cùng tìm hiểu qua tính chất và những thông tin liên quan.
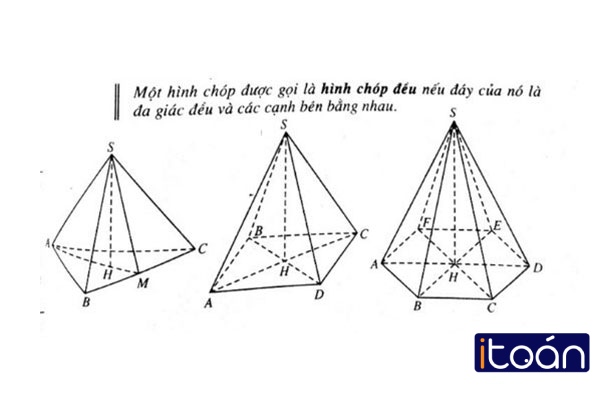
2. Tính chất hình chóp đều
Để hiểu rõ tính chất của hình chóp đều cần phân biệt rõ giữa hình chóp tam giác đều và tứ giác đều.
Về cơ bản, tính chất của loại hình này bao gồm những yếu tố sau:
- Hình chóp tam giác đều có tính chất là hình có 3 mặt phẳng nằm đối xứng với nhau.
- Các cạnh bên của hình chóp tam giác đều bằng nhau và có đáy là hình tam giác đều.
- Chân đường cao của hình chóp trùng với trọng tâm của mặt đáy.
- Mọi góc của hình chóp được tạo nên bởi mặt bên cũng như mặt đáy đều bằng nhau.
- Các góc được tạo nên bởi mặt đáy cũng như cạnh bên đều bằng nhau.
Một trong những tính chất quan trọng khác trong chương trình đó chính là kiến thức liên quan đến hình chóp tứ giác đều. Tính chất hình chóp tứ giác đều bao gồm những yếu tố sau:
- Đáy của hình chóp tứ giác đều là hình vuông.
- Các cạnh bên đều bằng nhau.
- Các mặt bên của hình chóp tứ giác đều là những tam giác cân bằng nhau.
- Chân đường cao của hình chóp trùng với giao điểm 2 đường chéo của mặt đáy.
- Tất cả những góc được tạo ra từ cạnh bên cũng như mặt đáy đều bằng nhau.
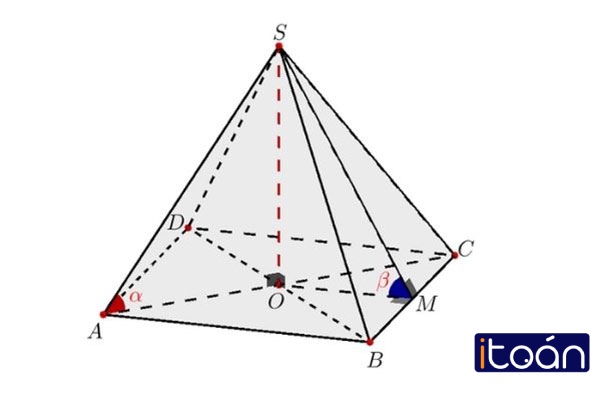
3. Hướng dẫn vẽ dựa vào tính chất hình chóp đều
Hình chóp đều là một trong những kiến thức hình học không gian trọng tâm trong chương trình trung học phổ thông. Để vẽ được chúng cần phụ thuộc vào các đặc tính cụ thể của loại hình này. Đối với hình chóp tứ giác đều cũng như tam giác đều thì các vẽ sẽ khá giống nhau và được thực hiện như sau:
- Bước 1: Tiến hành vẽ đáy hình chóp là hình vuông hoặc hình tam giác. Đối với hình chóp tứ giác đều thì vẽ đáy là hình vuông và hình chóp tam giác đều thì vẽ đáy là hình tam giác đều.
- Bước 2: Xác định tâm của mặt phẳng đáy, tâm của mặt phẳng đáy cũng chính là chân đường cao theo như tính chất hình chóp đều.
- Bước 3: Từ chân đường cao hình chóp kéo một đường thẳng nhất định để xác định đỉnh của hình chóp đều.
- Bước 4: Tiến hành vẽ những cạnh bên sao cho chúng đều bằng nhau. Vẽ cạnh bên bằng cách nối từ đỉnh hình chóp xuống góc đáy của hình chóp để tạo thành những cạnh bên là những tam giác đều và bằng nhau.
- Bước 5: Những góc tạo được bởi mặt đáy và cạnh bên của mặt đáy là bằng nhau
4. Cách tính diện tích của hình chóp đều:
a. Diện tích xung quanh hình chóp đều:
Dựa vào tính chất hình chóp đều ta có công thức tính diện tích xung quanh của hình chóp đều là tích của trung đoạn của hình chóp đều nhân với nửa chu vi đáy.
Công thức tổng quát tính diện tích xung quanh của hình chóp đều:
- Sxq=p×d
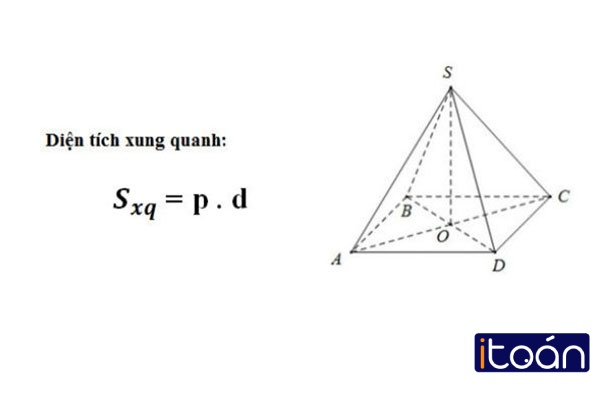
Trong đó:
- d là trung đoạn
- p là nửa chu vi đáy.
- Sxq: Diện tích xung quanh
b. Diện tích toàn phần hình chóp đều
Dựa vào tính chất hình chóp đều ta có công thức tính diện tích toàn phần của hình chóp đều là tổng của diện tích xung quanh và diện tích đáy.
Công thức tổng quát tính diện tích toàn phần của hình chóp đều:
- Stp=Sxq+Sđáy
Trong đó:
- Sđáy là diện tích mặt đáy
- Sxq: Diện tích xung quanh
- Stp: Diện tích toàn phần
Đối với diện tích đáy cần tùy thuộc vào dạng đáy mà áp dụng những công thức tính khác nhau.
5. Cách tính thể tích hình chóp đều:
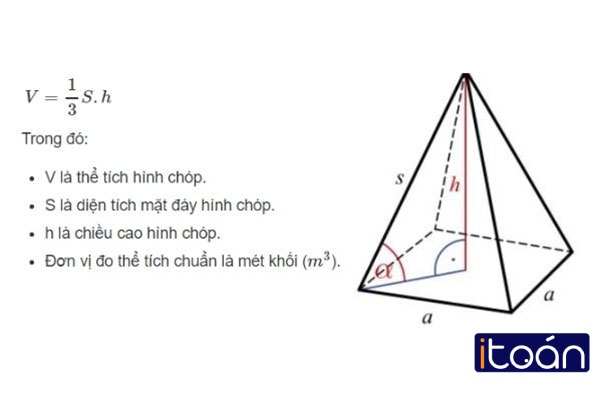
Để tính được thể tích hình chóp đều cần phụ thuộc vào các đặc tính của loại hình này như đã được nêu ở phía trên bài viết. Theo đó công thức tính thể tích hình chóp đều là tích của ⅓ diện tích đáy nhân với chiều cao.
Công thức tổng quát tính thể tích hình chóp đều cụ thể là:
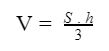
Trong đó:
- S là diện tích đáy và tùy thuộc vào mỗi hình đáy mà có những công thức tính diện tích đáy khác nhau.
- h là chiều cao.
- V là thể tích.
Bài giảng trên đã cung cấp đầy đủ tính chất hình chóp đều cũng như công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp. Hy vọng đây sẽ là những kiến thức bổ ích dành cho các em học sinh khi làm bài tập và quý phụ huynh có nhu cầu giảng dạy và ôn tập cho con em của mình.
>> Xem thêm: Tổng hợp công thức tính diện tích, thể tích hình lăng trụ đứng
