Tính chất 3 đường phân giác của tam giác – Toán 7

Bài học hôm trước các em đã được biết thế nào là tia phân giác của 1 góc, hôm nay chúng ta sẽ ứng dụng nó trong tam giác: Tính chất 3 đường phân giác của tam giác. Trong 1 tam giác thì ba đường phân giác có những tính chất gì, chúng có mối liên hệ với nhau như thế nào, cùng iToan tìm hiểu nhé!
Mục tiêu học trong bài:
- Ghi nhớ đường phân giác của tam giác và biết số lượng đường phân giác mỗi tam giác.
- Định lý đường phân giác của một tam giác cân.
- Vận dụng định lý này để giải toán.
Tính chất ba đường phân giác trong tam giác
Đường phân giác trong tam giác
-
-
-
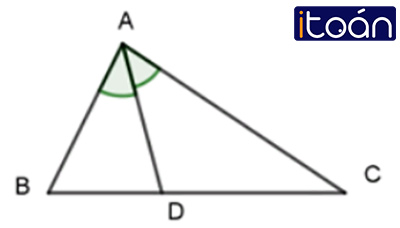
- Trong tam giác ABC, đường phân giác của góc A giao với BC tại điểm D, khi đó AD được gọi là đường phân giác (từ đỉnh A) của tam giác ABC. Đường thẳng AD còn được gọi là đường phân giác của tam giác ABC.
- Mỗi tam giác đều có ba đường phân giác.
-
-
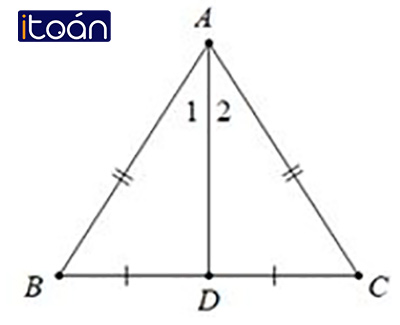
Tính chất: Trong tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời cũng là đường trung tuyến ứng với cạnh đáy.
- Giả thiết: ΔABC,AB=AC;A1ˆ=A2ˆ
- Kết luận: BD=DC
Tính chất ba đường phân giác trong tam giác
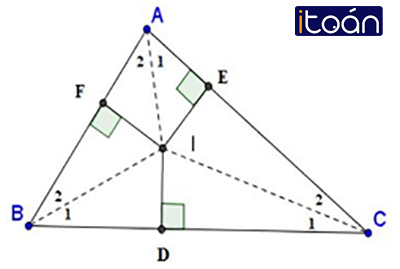
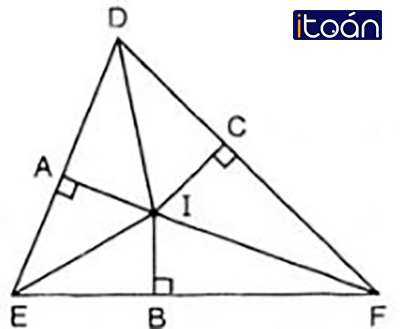
Đinh lý: Ba đường phân giác của một tam giác cùng đi qua một điểm và điểm này cách đều ba cạnh của tam giác đó.
-
-
-
- Giả thiết: Tam giác ABC có ba đường phân giác giao nhau tại I
- Kết luận: ID=IE=IF.
-
-
Ví dụ:
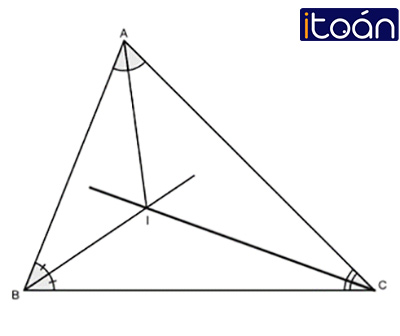
I là giao điểm của hai đường phân giác của góc B và góc C. Chứng minh:
BICˆ=90∘+Aˆ2
Giải:
Ta có: Aˆ+Bˆ+Cˆ=180∘ ( định lý tổng ba góc trong tam giác )
⇒Aˆ2+Bˆ2+Cˆ2=90∘.
⇒Bˆ2+Cˆ2=90∘−Aˆ2.
Mà BI là phân giác của góc ABC nên IBCˆ=B^2.
Góc ACB có CI là tia phân giác nên ICBˆ=Cˆ2. Trong tam giác BIC có:
BICˆ+IBCˆ+ICBˆ=180∘ ( định lý tổng ba góc trong tam giác).
⇒BICˆ=180∘−(IBCˆ+ICBˆ)
⇒BICˆ=180∘−(Bˆ2+Cˆ2)=180∘−(90∘−Aˆ2)=90∘+Aˆ2
Vậy BICˆ=90∘+Aˆ2.
Cùng xem video bài giảng để làm các ví dụ trực quan nhé!
Lời giải bài tập sách giáo khoa trang 72
Bài 36: Trang 72 – SGK Toán 7
Cho tam giác DEF, điểm I thuộc tam giác này và cách đều ba cạnh của nó. Chứng minh I là giao điểm của ba đường phân giác tam giác DEF.
Bài Làm:
Từ I ta kẻ IA ⊥ DE; IB ⊥ EF và IC ⊥ DF.
Vì I cách đều hai cạnh DE và DF nên I thuộc đường phân giác của góc EDF (định lí 2 – định lí đảo của tia phân giác)
Tương tự ta có điểm I thuộc tia phân giác của góc DEF và góc EFD.
Vậy I là giao điểm ba đường phân giác trong tam giác DEF.
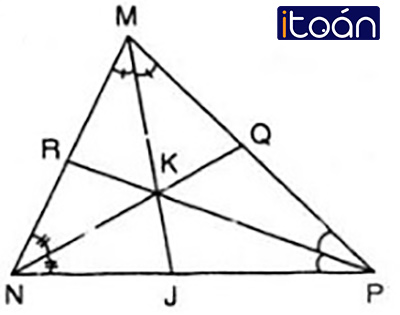
Bài 37: Trang 72 – SGK Toán 7
Nêu cách vẽ điểm K thuộc tam giác MNP sao cho khoảng cách từ K đến ba cạnh của tam giác bằng nhau. Vẽ hình minh họa.
Bài Làm:
Cách vẽ
Vẽ phân giác MJ của góc M, phân giác NQ của góc N. Giao điểm của hai tia phân giác chính là điểm K cần tìm.
Chứng minh
Vì K là giao điểm của hai phân giác của tam giác MNP nên K cách đều ba cạnh của tam giác (theo định lí giao điểm của ba đường phân giác.)
Bài 38: Trang 73 – SGK Toán 7
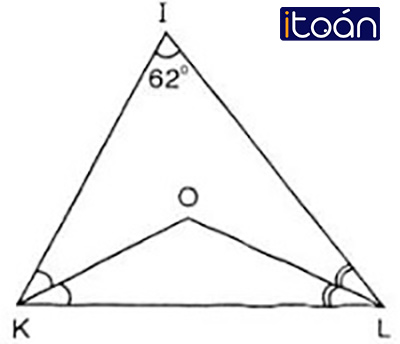
Cho hình 38.
a) Tính số đo góc KOL.
b) Kẻ tia IO, hãy tính số đo góc KIO.
c) Điểm O có cách đều ba cạnh của tam giác IKL không? Tại sao?
Bài Làm:
a) ∆KIL có Iˆ=620
nên IKLˆ+ILKˆ=1180
- Vì KO và LO là phân giác IKLˆ, ILKˆ
nên OKLˆ+OLKˆ=12.(IKLˆ+ILKˆ)
=> OKLˆ+OLKˆ=12.1180
=> OKLˆ+OLKˆ=590
- ∆KOL có OKLˆ+OLKˆ=590
nên KOLˆ=1800−590=1210
b) ΔKIL có O là điểm chung của hai đường phân giác KO và LO => OI là phân giác của góc KIL (định lí ba đường phân giác cùng đi qua một điểm).
Vậy: KIOˆ=1/2.KILˆ=1/2.62=31
c) O là giao điểm hai đường phân giác của Kˆ và Lˆ nên O cách đều ba cạnh của tam giác IKL.
Bài 39: Trang 73 – SGK Toán 7
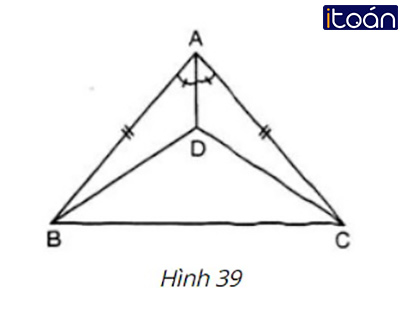
Cho hình 39.
a) Chứng minh ΔABD = ΔACD
b) So sánh 2 góc DBC và DCB.
Bài Làm:
a) Xét ΔABD và ΔACD có:
AB=AC (gt)
BADˆ=CADˆ (gt)
AD chung
⇒ΔABD=ΔACD (c−g−c) (đpcm)
b) Từ câu a) ta có: ΔABD=ΔACD
⇒BD=CD (cạnh tương ứng)
⇒ΔBDC cân tại D
⇒DBCˆ=DCBˆ (đpcm)
Bài 40: Trang 73 – SGK Toán 7
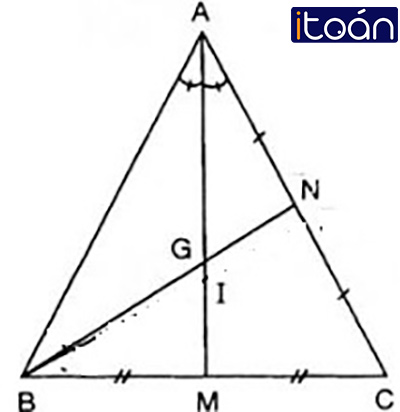
Tam giác ABC cân tại A có G là trọng tâm, I thuộc tam giác và cách đều ba cạnh của tam giác. Chứng minh A, G, I thẳng hàng.
Bài Làm:
Gọi M, N lần lượt là trung điểm của BC và AC.
- G là trọng tâm tam giác nên G nằm trên trung tuyến AM (1).
- I cách đều ba cạnh của tam giác => I là giao điểm ba đường phân giác trong của ΔABC.
- ΔABC cân nên đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến (tính chất).
Do đó, I thuộc AM (2).
Từ (1) và (2) => ba điểm A, G, I thẳng hàng (đpcm).
Bài 41: Trang 73 – SGK Toán 7
Trọng tâm của tam giác đều có cách đều ba cạnh của nó không? Giải thích?
Bài Làm:
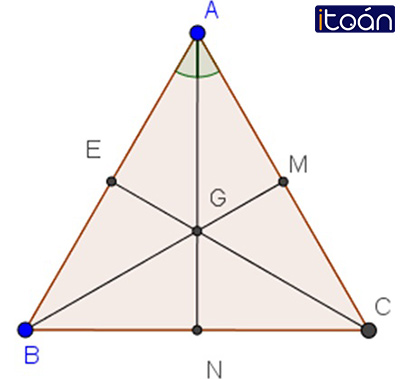
⇒GA=23,AN;GB=23.BM;GC=23.EC (tính chất đường trung tuyến trong tam giác)
∆ABC đều => AN= BM=CE
⇒GA=GB=GC (vì cùng bằng 2/3 các đoạn bằng nhau)
Xét ΔAMG và ΔCMG có:
GM chung
AM=MC (M là trung điểm AC)
AG=CG (cmt)
⇒ΔAMG=ΔCMG (c.c.c)
⇒AMGˆ=CMGˆ
Mà AMGˆ+CMGˆ=1800
⇒AMGˆ=900
⇒GM⊥AC tức là GM khoảng cách từ G đến AC.
Tương tự GE, GN là khoảng cách từ G đến AB, BC.
Mà GM=13.BM;GN=13.AN;EG=13.EC
Và AN=BM=EC nên GM=GN=GE.
Hay G cách đều ba cạnh của tam giác ABC.
Bài 43: Trang 73 – SGK Toán 7
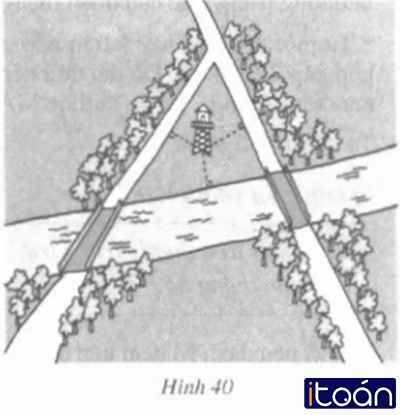
Đố: Hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau (h.40).
Tìm một địa điểm để xây đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông đều bằng nhau.
Có tất cả bao nhiêu điểm như vậy?
Bài Làm:
Ta thấy hai con đường cắt nhau và cùng cắt con sông tạo thành tam giác ABC.
- Địa điểm để xây đài quan sát phải là giao điểm I của 3 đường phân giác trong tam giác ABC.
- Giao điểm I’ của hai phân giác ngoài của góc B và C cũng thỏa mãn đề bài.
Vậy tìm được 2 điểm để xây đài quan sát là I và I’.
Bài tập tự luyện Tính chất 3 đường phân giác của 1 tam giác
Phần câu hỏi
Câu 1: Cho tam giác ΔABC cân tại A có I là giao điểm của 3 đường phân giác. Chọn kết luận đúng.
A. IC=IA
B. I là trọng tâm của tam giác ABC
C. IB=IA
D. Khoảng cách từ I đến ba đường thẳng AB,CB,CA bằng nhau
Câu 2: Cho tam giác ΔABC, M là một điểm nằm trong tam giác. Chọn phát biểu đúng:
A. M cách đều ba cạnh của tam giác khi và chỉ khi M là giao điểm của ba đường phân giác
B. Điểm M cách đều ba cạnh của tam giác ABC
C. MA=MB=MC
Câu 3: Cho △ABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có
A. I cách đều ba đỉnh của △ABC
B. A,I,G thẳng hàng
C. G cách đều ba cạnh của △ABC
Câu 4: Cho tam giác MNP có Mˆ=70o;Pˆ=60o . S là giao điểm của các đường phân giác MI và PK . Tính số do góc SNP
A. 25
B. 35
C. 60
D. 30
Phần đáp án
1. D 2.A 3.B 4.A
Lời kết
Những tính chất ba đường phân giác của tam giác rất quan trọng và được ứng dụng nhiều trong các bài toán hình học sau này. Để ôn luyện thêm cũng như nâng cao kiến thức, các em có thể nhờ đến sự trọ giúp của nền tảng học trực tuyến Toppy. Toppy với đội ngũ thầy cô giáo trẻ, giỏi chuyên môn , cùng với phưng pháp học tập mới mẻ sẽ giúp các em hứng thú hơn trong quá trình học tập.
>> Xem thêm bài giảng iToan: