Tính chất tia phân giác của 1 góc – Toán lớp 7

Bài giảng: Tính chất tia phân giác của 1 góc– nằm trong phần kiến thức hình học cơ bản của Toán lớp 7 tập 2. Bài giảng được các thầy cô iToan biên soạn với lý thuyết dễ hiểu& Hướng dẫn giải chi tiết bài tập sách giáo khoa, cuối cùng là các bài tập tự luyện giúp bạn ghi nhớ và thành thạo bài hơn.
Lý thuyết Tính chất tia phân giác của 1 góc
Định lý thuận
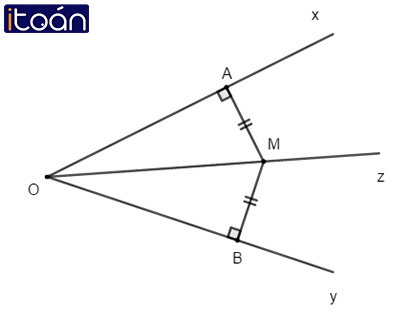
- Giả thiết: Oz là tia phân giác của xOyˆ. M∈Oz;MA⊥Ox;MB⊥Oy
- Kết luận: MA=MB.
Định lý đảo
-
-
-
- Giả thiết: M∈xOyˆMA⊥Ox;MB⊥OyMA=MB
- Kết luận: M∈ tia phân giác của xOyˆ.
- Nhận xét: Từ định lý thuận và địnnh lý đảo ta có: Tập hợp tất cả các điểm nằm trong một góc và cách đều hai cạnh của góc được gọi là tia phân giác của góc đó.
-
-
Ví dụ
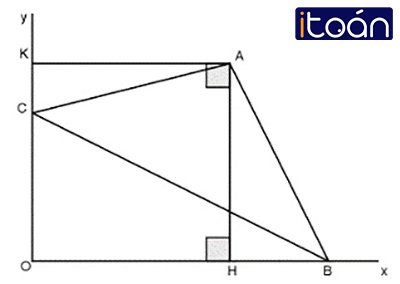
Ví dụ: Cho góc xOy vuông và tam giác ABC vuông cân tại A, có B∈Ox, C∈Oy, O và A thuộc hai nửa mặt phẳng đối nhau bờ BC. Chứng minh: OA là phân giác của góc xOy.
Giải:
Vẽ AH⊥Ox, AK⊥Oy.
Xét ΔKAC vuông tại K và ΔHAB vuông tại H.
Ta có:
KACˆ=HABˆ (do cùng là góc phụ với CAHˆ)
AC=AB (do tam giác ABC vuông cân tại A )
Do đó: △KAC=ΔHAB (cạnh huyền – góc nhọn)
⇒ AK=AH (cặp cạnh tương ứng bằng nhau)
Vậy OA là phân giác của góc xOyˆ.
Em hãy xem thêm video bài giảng dưới đây để hiểu bài và nhớ bài kĩ hơn!
Lời giải bài tập sách giáo khoa Tính chất tia phân giác của 1 góc
Bài 31: Trang 70 – SGK Toán 7
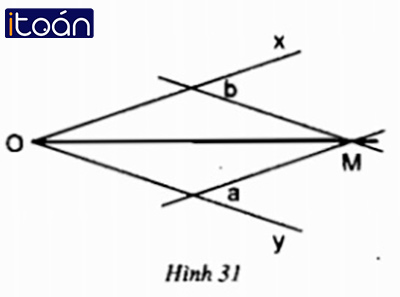
Hình 31 hướng dẫn cách thước hai lề để vẽ tia phân giác của góc xOy:
- Áp một lề của thước trùng vào cạnh Ox, kẻ đường thẳng a theo lề còn lại của thước.
- Tương tự, làm với cạnh Oy, ta sẽ kẻ được đường thẳng b.
- Gọi M là giao điểm của a và b, ta đã vẽ được OM là tia phân giác của góc xOy.
Chứng minh tia OM đúng là tia phân giác của góc xOy.
(Gợi ý: Dựa vào bài tập 12 sách giáo khoa Toán 7 để chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (đều bằng khoảng cách hai lề của chiếc thước) sau đó áp dụng định lí 2.
Bài Làm:
Gọi A, B lần lượt là chân đường cao hạ từ điểm M xuống Ox, Oy => MA, MB lần lượt là khoảng cách từ điểm M đến Ox, Oy.
Ta có tính chất độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.
Suy ra: MA = MB (đều bằng khoảng cách hai lề của thước) hay M cách đều hai cạnh Ox, Oy.
Theo định lý 2 suy ra: OM là tia phân giác của góc xOy.
Bài 32: Trang 70 – SGK Toán 7
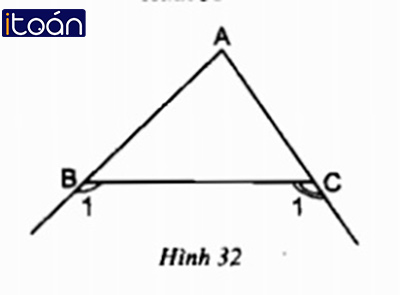
Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
Bài Làm:
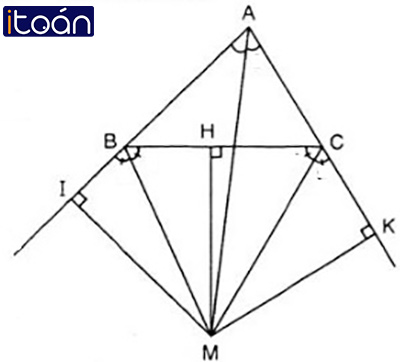
Gọi điểm M là giao điểm hai tia phân giác của hai góc ngoài B và C của ΔABC.
Ta kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
Vì M nằm trên tia phân giác của góc B1 suy ra MH = MI
Vì M nằm trên tia phân giác của góc C1 suy ra MH = MK
=> MI = MK
Vậy M thuộc phân giác của góc A (Định lí 2)
Bài 33: Trang 70 – SGK Toán 7
Cho O là giao điểm của hai đường thẳng xx’, yy’
a) Chứng minh hai tia phân giác Ot, Ot’ của một cặp góc kề bù tạo với nhau một góc vuông.
b) Chứng minh: Nếu điểm M thuộc đường thẳng Ot hoặc Ot’ thì M cách đều các đường thẳng xx’ và yy’.
c) Chứng minh: Nếu M cách đều hai đường thẳng xx’, yy’ thì M thuộc đường thẳng Ot hoặc Ot’.
d) Khi M ≡ O thì khoảng cách từ M đến xx’ và yy’ là bao nhiêu?
e) Hãy nhận xét về tập hợp các điểm cách đều hai đường thẳng xx’, yy’.
Bài Làm:
a)

nên yOtˆ=xOtˆ=12xOyˆ
Ot’ là phân giác của xOy′ˆ
nên xOt′ˆ=y′Ot′ˆ=12.xOy′ˆ
⇒xOtˆ+xOt′ˆ=12.xOyˆ+12.xOy′ˆ=12.(xOyˆ+xOy′ˆ)
mà xOyˆ+xOy′ˆ=1800 (2 góc kề bù)
=> xOtˆ+xOt′ˆ=12.1800=900
Vậy hai tia phân giác của hai góc kề bù tạo với nhau một góc vuông.
Các em đã làm đúng phần a chưa, chúng ta cùng làm tiếp phần b nhé!
b) Nếu M thuộc Ot hoặc Ot’ thì M cách đều hai đường thẳng xx’ và yy’
Thật vậy: M ∈ Ot do Ot là phân giác của xOyˆ nên M cách đều Ox, Oy.
=> M cách đều xx’, yy’
M ∈ Ot’ do Ot’ là phân giác của xOy′ˆ nên M cách đều xx’, yy’.
=> M cách đều xx’, yy’.
c) Nếu M cách đều hai đường thẳng xx’, yy’ và giả sử M nằm trong một góc trong bốn góc xOyˆ, xOy′ˆ, x′Oy′ˆ, x′Oyˆthì M phải thuộc phân giác của góc ấy. (áp dụng định lí 1)
Tức M phải thuộc Ot hoặc Ot’
d) Khi M ≡ O thì khoảng cách từ M đến xx’, yy’ bằng 0
e) Nhận xét rút ra được: Tập hợp các điểm cách đều hai đường thẳng cắt nhau xx’, yy’ thuộc hai đường thẳng vuông góc với nhau là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
Bài 34: Trang 71 – SGK Toán 7
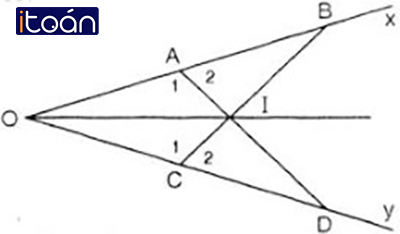
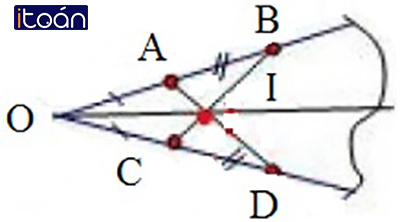
Cho góc xOy không phải góc bẹt. Trên tia Ox ta lấy hai điểm A và B, trên tia Oy ta lấy hai điểm C và D để OA = OC, OB = OD. Gọi I là giao điểm của AD và BC. Chứng minh:
a) BC = AD;
b) IA = IC, IB = ID;
c) OI là tia phân giác của góc xOy.
Bài Làm:
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
xOyˆ là góc chung
=> ∆AOD = ∆COB (c-g-c)
=> AD = BC (cạnh tương ứng)
b) ∆AOD = ∆COB (cmt)
=> AODˆ=OCBˆ
Mà: BAIˆ kề bù góc AODˆ; DCIˆ kề bù góc OCBˆ
=> BAIˆ=DCIˆ (2 góc kề bù với hai góc bằng nhau)
Xét: ∆DIC và ∆BIA có:
CD = AB (vì: OD = OB; OC = OA)
DCIˆ=ABIˆ ( 2 góc tương ứng của ∆AOD = ∆COB)
BAIˆ=DCIˆ (cmt)
=> ∆DIC = ∆BIA (g-c-g)
=> IC = IA và ID = IB.
c) Xét ∆OAI và ∆OCI có:
OA = OC (gt)
OI chung
IA = IC (cmt)
=> ∆OAI = ∆OCI (c.c.c)
=> COIˆ=AOIˆ
=> OI là phân giác của xOyˆ
Bài 35: Trang 71 – SGK Toán 7
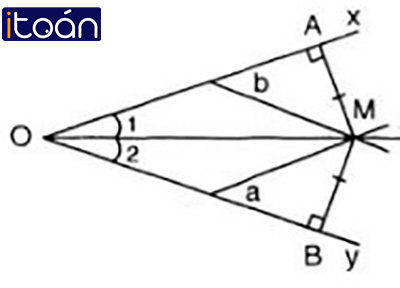
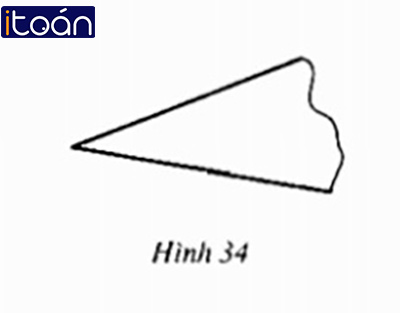
Cho một mảnh sắt phẳng có hình dạng một góc (h.34) và một chiếc thước thẳng có chia vạch. Làm cách nào để vẽ được tia phân giác của góc này một cách chính xác?
Gợi ý: Áp dụng bài tập 34.
Bài Làm:
- Gọi O là góc của mảnh sắt
- Trên cạnh thứ nhất ta lấy hai điểm phân biệt A, B; trên cạnh thứ hai lấy hai điểm C, D để OA = OC và OB = OD.
- Gọi I là giao điểm của 2 đoạn thẳng AD và BC. Đường thẳng OI là tia phân giác của góc này.
Chứng minh
- ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
xOyˆ là góc chung
=> ∆AOD = ∆COB (c-g-c)
=> AD = BC (cạnh tương ứng)
- Vì: ∆AOD = ∆COB (cmt)
=> AODˆ=OCBˆ
Mà: BAIˆ kề bù góc AODˆ; DCIˆ kề bù góc OCBˆ
=> BAIˆ=DCIˆ (2 góc kề bù với hai góc bằng nhau)
- Xét: ∆DIC và ∆BIA có:
CD = AB (vì: OD = OB; OC = OA)
DCIˆ=ABIˆ ( 2 góc tương ứng của ∆AOD = ∆COB)
BAIˆ=DCIˆ (cmt)
=> ∆DIC = ∆BIA (g-c-g)
=> IC = IA và ID = IB.
- Xét ∆OAI và ∆OCI có:
OA = OC (gt)
OI chung
IA = IC (cmt)
=> ∆OAI = ∆OCI (c.c.c)
=> COIˆ=AOIˆ
=> OI là phân giác của xOyˆ
=> OI là phân giác của xOyˆ
Bài tập tự luyện Tính chất tia phân giác của 1 góc
Phần câu hỏi
Câu 1: Chọn nhận định đúng về tính chất 2 tia phân giác của hai góc kề bù:
A. Hai tia phân giác của hai góc kề bù tạo với nhau góc 450
B. Hai tia phân giác của hai góc kề bù vuông góc với nhau
C. Hai tia phân giác của hai góc kề bù tạo với nhau góc 600
Câu 2: Điểm E nằm trên tia phân giác góc A của tam giác ABC ta có:
A. E nằm trên tia phân giác góc B
B. E cách đều hai cạnh AB,AC
C. E nằm trên tia phân giác góc C
Câu 3: Cho điểm M nằm trên tia phân giác At của góc xAy nhon. Kẻ MH⊥Ax ở H và MK⊥Ay ở K. So sánh MH và MK.
A. MH=MK
B. MH<MK
C. MH>MK
Câu 4: Lựa chọn phát biểu đúng:
A. HL là trung tuyến ứng với cạnh IK của tam giác HIK
B. HL là phân giác ứng với góc H của tam giác HIK
C. HL là đường cao ứng với cạnh IK của của tam giác HIK
Phần đáp án
1.B 2.B 3.A 4.
Lời kết
Qua bài học này, các em đã ghi nhớ hết tính chất và cách giải bài tập liên quan đến tính chất tia phân giác của 1 góc chưa? Để học tốt môn toán và nhiều môn học khác trong chương trình lớp 7, em có thể tìm hiểu về các khóa học trên Toppy. Toppy luôn nỗ lực đem đến cho học sinh những kiến thức bổ ích và những trải nghiệm học tập tốt nhất.
>> Xem thêm: