Tổng hợp kiến thức lý thuyết về Vị trí tương đối của hai đường tròn

Trong chương trình lớp 9, các em sẽ gặp một bài học về vị trí tương đối của hai đường tròn. Bài học này vô cùng quan trọng không chỉ ở trong chương học của lớp 9 mà còn trong các bài thi chuyển cấp. Chính vì thế, hôm nay Itoan sẽ giới thiệu cho các em lý thuyết và một số dạng bài tập thường gặp, hướng dẫn cách làm qua đó giúp các em qua môn và vượt cấp dễ dàng hơn nhé.

Đường nối tâm

Trước tiên, chúng ta sẽ xem đường nối tâm là đường như thế nào. Cùng xét hai đường tròn có tâm không trùng nhau, trong đó O là tâm của hình tròn số 1 và O’ là tâm của đường tròn số 2. Đường nối tâm chính là đường thẳng giữa tâm O và tâm O’. Và đoạn nối tâm chính là đoạn OO’. 

Hơn thế nữa, đường kính là trục đối xứng của mỗi đường tròn nên đường nối tâm cũng chính là trục đối xứng của hình gồm hai đường tròn đó

Ba vị trí tương đối của hai đường tròn

Khi xét vị trí tương đối của hai đường tròn (O;R) và (O’, r) R>r; chúng ta tìm thấy ba vị trí tương đối như sau:

Hai đường tròn cắt nhau

Đây là vị trí đầu tiên được nhắc đến khi nói về vị trí tương đối của 2 hình tròn. 

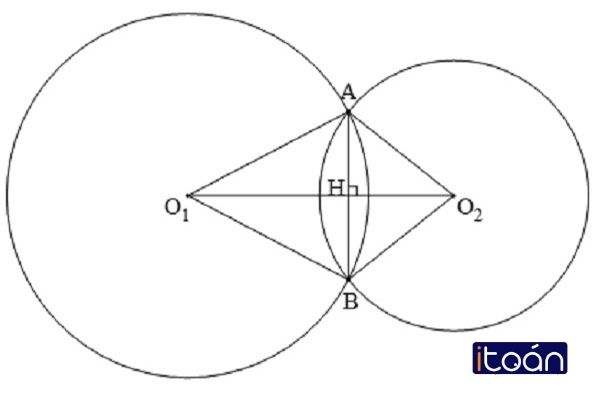
Hai đường tròn cắt nhau khi có hai điểm chung. Trong trường hợp này A và B là hai giao điểm, đoạn thẳng AB là dây chung, O1, O2 là đường nối tâm, đoạn thẳng O1O2 là đoạn nối tâm. Khi đặt O1A = R; O2A = r khi đó: |R – r| < O1O2 < R + r. 

Cũng theo tính chất của vị trí tương đối nêu ở trên, đường nối tâm là đường trung trục của dây chung.

Hai đường tròn tiếp xúc nhau

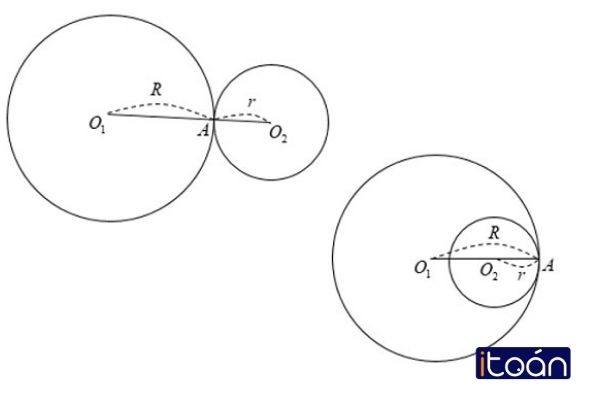
Một vị trí tương đối khác chính là hai đường tròn tiếp xúc nhau. Trong trường hợp này, có thể vẽ thành 2 trường hợp. Một trường hợp chính là hai đường tròn không thuộc nhau và có tiếp xúc tại 1 điểm. Trường hợp thứ hai chính là đường tròn (O2,r) thuộc đường tròn (O1,R) và có tiếp xúc tại 1 điểm A.

Như vậy, hai đường tròn tiếp xúc nhau khi nó có 1 điểm chung duy nhất. Khi đó, A được gọi là tiếp điểm. Và hai trường hợp ở trên được gọi như sau: trường hợp 1 là tiếp xúc ngoài tại A: O1O2 = R + r và tiếp xúc trong tại A: O1O2 = |R – r|.

Hai đường tròn không giao nhau

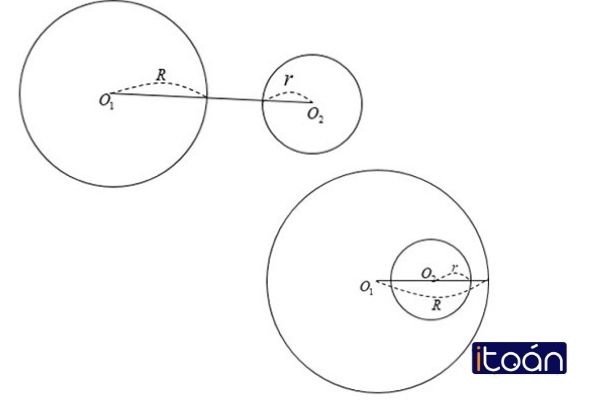
Vị trí tương đối thứ ba có thể gặp chính là hai đường tròn không hề giao nhau, tức là không có bất kỳ một điểm chung nào.

Có 3 trường hợp xảy ra, hoặc là hai đường tròn ngoài nhau: O1O2 > R + r; hoặc là hai đường tròn đựng nhau: O1O2 < |R – r|; hoặc là hai đường tròn đồng tâm O1O2 = 0.

Ba vị trí tương đối của đường thẳng và đường tròn

Tương tự như vị trí tương đối của hai đường tròn, toán 9 vị trí tương đối của đường thẳng và đường tròn cũng có 3 vị trí như sau:

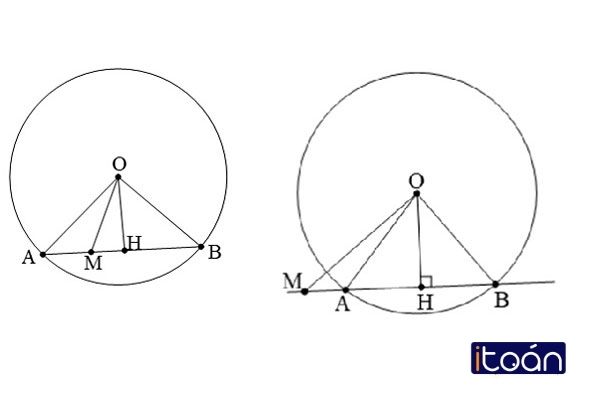
• Đường thẳng và đường tròn cắt nhau: Xảy ra khi đường thẳng có 2 điểm chung với đường tròn. Lúc này, đường thẳng cắt đường tròn ở 2 vị điểm  phân biệt

• Đường thẳng và đường tròn tiếp xúc nhau: xảy ra khi đường thẳng có một điểm chung với đường tròn.
• Đường thẳng và đường tròn không giao nhau: lúc này, đường thẳng và đường tròn không có điểm chung. Khi đó OH>R.

Tiếp tuyến chung của hai đường tròn

Một nội dung tiếp theo trong bài học vị trí tương đối của hai đường tròn chính là hiểu về định nghĩa của tiếp tuyến chung của hai đường tròn. Ở đây có thể hiểu là đường thẳng tiếp xúc với cả hai đường tròn đó.

Tiếp tuyến chung trong là tiếp tuyến chung cắt đoạn nối tâm. Tiếp tuyến chung ngoài là tiếp tuyến chung không cắt đoạn nối tâm.

Số tiếp tuyến chung của hai đường tròn ở một số vị trí tương đối như sau:

• Hai đường tròn cắt nhau: 2 tiếp tuyến chung ngoài.
• Hai đường tròn tiếp xúc ngoài: 2 tiếp tuyến chung ngoài và 1 tiếp tuyến chung trong.
• Hai đường tròn tiếp xúc trong: 1 tiếp tuyến chung.
• Hai đường tròn ở ngoài nhau: 2 tiếp tuyến chung ngoài và 2 tiếp tuyến chung trong.
• Hai đường tròn chứa nhau và hai đường tròn đồng tâm: không có tiếp tuyến chung.

Các dạng bài tập phổ biến

Với bài học này, có 4 dạng bài phổ biến như sau:

Dạng 1: Xác định vị trí tương đối của hai đường tròn

Với dạng bài 1, phương pháp giải chính là xác định độ dài đoạn nối tâm, sau đó xác định hệ thức liên hệ giữa độ lớn các bán kính và độ dài đoạn nối tâm

Dạng 2: Bài toán với hai đường tròn tiếp xúc nhau

Bài toán vẽ hình cũng khá phổ biến trong các bài tập liên quan. Để làm được bài toán này, các em cần vẽ đường nối tâm, sử dụng tính chất của tiếp điểm trên đường nối tâm; đường nối tâm là trục đối xứng của hình gồm cả hai đường tròn, sử dụng hệ thức là độ dài đoạn nối tâm.

Trong trường hợp cần thiết, các em cũng có thể vẽ tiếp tuyến chung tại tiếp điểm để sử dụng tính chất đặc trưng của hai tiếp tuyến cắt nhau.

Dạng 3: Bài toán với hai đường tròn cắt nhau

Để giải được các bài toán dạng này, các em vẽ dây chung, vẽ đường nối tâm. Sau đó, chỉ cần sử dụng tính chất của đường nối tâm là trung trực của dây chung là ra đáp án. Bài toán này các em chỉ cần nắm vững kiến thức lý thuyết là có thể giải được.

Dạng 4: Chứng minh các quan hệ hình học (song song, vuông góc, thẳng hàng…)

Đây là dạng bài tương đối phổ biến và các em thường gặp. Lúc này, hãy xác định vị trí tương đối của hai hình tròn xem nó thuộc vị trí nào. Sau đóm hãy vận dụng các tính chất chung của tiếp tuyến, tiếp tuyến chung, dây vuông góc… để giải.

Như vậy, kiến thức của vị trí tương đối của hai đường tròn khá dài, mỗi vị trí lại có định nghĩa, đặc trưng riêng. Vì thế các em đừng nhầm lẫn các vị trí với nhau nhé.