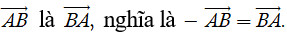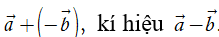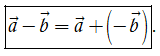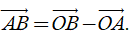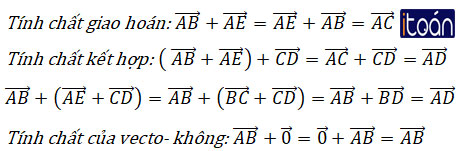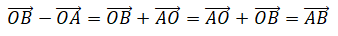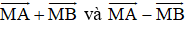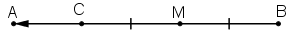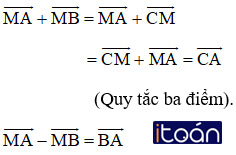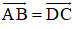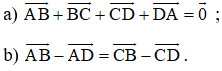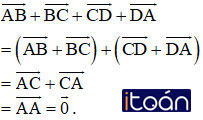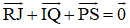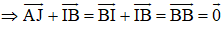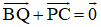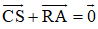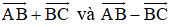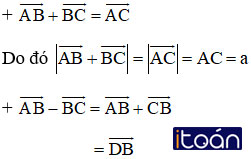Tổng và hiệu hai Vecto – Học toán cùng itoan

Bài học hôm nay sẽ giới thiệu đến các bạn một phần kiến thức mới thuộc chương trình Toán lớp 10, đó là Tổng và hiệu hai Vecto. Đây là kiến thức trọng tâm của bài học ngày hôm nay. Trong bài này, các em sẽ được tìm hiểu về định nghĩa của Tổng và hiệu hai Vecto và cách làm sao để tính Tổng và hiệu hai Vecto. Nội dung bài học tuy khó nhưng các em đừng nản nhé vì đây là bài quan trọng trong việc kiểm tra và thi cử sau này. Do đó, các em hãy tập trung học bài và ghi chú nhé. Không để các em đợi lâu nữa. Nào cùng vào bài học ngay với iToan thôi!
Mục tiêu bài học
Dưới đây là các mục tiêu bài học các em cần đạt được sau buổi học ngày hôm nay. Cùng cố gắng với itoan nhé!
Dưới đây là các mục tiêu mà các cô trò mình sẽ cố gắng đạt được sau buổi học.
- Nắm được kiến thức lý thuyết Tổng và hiệu hai Vecto
- Áp dụng lý thuyết vào bài tập
- Nắm được cách làm bài tập nâng cao
Lý thuyết
1. Tổng của hai vectơ
a. Định nghĩa.
Cho hai vectơ
Lấy một điểm A tùy ý, vẽ 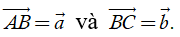
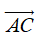
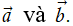
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
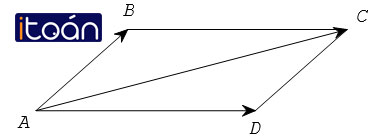
2. Quy tắc hình bình hành
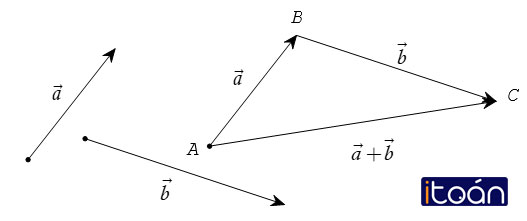
Nếu ABCD là hình bình hành thì
3. Tính chất của phép cộng các vectơ
Với ba vectơ 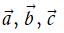
(tính chất giao hoán);
(tính chất kết hợp);
(tính chất của vectơ – không).
4. Hiệu của hai vectơ
a) Vectơ đối
Cho vectơ 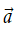
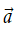
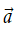
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của
Đặc biệt, vectơ đối của vectơ 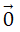
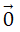
b) Định nghĩa hiệu của hai vectơ
Định nghĩa
Cho hai vectơ
Ta gọi hiệu của hai vectơ 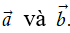
Như vậy:
Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có
c) Chú ý:
- Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.
- Với ba điểm tùy ý A, B, C ta luôn có
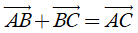
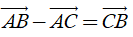
5. Áp dụng
a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi
b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi
Bài tập sách giáo khoa
Bài 2 trang 9:
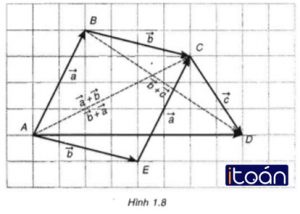
Hãy kiểm tra các tính chất của phép cộng trên hình 1.8.
Hướng dẫn giải:
Bài 2 trang 10:
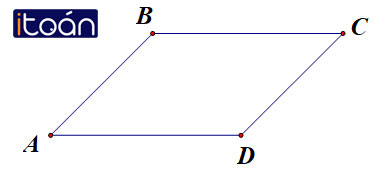
Vẽ hình bình hành ABCD. Hãy nhận xét về độ dài và hướng của hai vectơ AB→ và CD→
Hướng dẫn giải:
Về độ dài: hai vectơ AB→ và CD→ có cùng độ dài
Về hướng: hai vectơ AB→ và CD→ có hướng ngược nhau.
Bài 2 trang 11:
Hãy giải thích vì sao hiệu của hai vectơ OB→ và OA→ là vectơ AB→.
Hướng dẫn giải:
Bài 1 (trang 12 SGK Hình học 10):
Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vector
Hướng dẫn giải:
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy 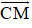
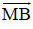
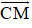
Khi đó:
Bài 2 (trang 12 SGK Hình học 10):
Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh rằng
Ta có: ABCD là hình bình hành nên
Bài 3 (trang 12 SGK Hình học 10):
Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
Hướng dẫn giải:
a) Ta có:
b) Áp dụng quy tắc trừ hai vec tơ ta có:
Bài 4 (trang 12 SGK Hình học 10):
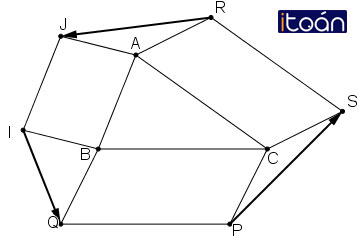
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành: ABIJ, BCPQ, CARS. Chứng minh rằng
Hướng dẫn giải:
Ta có:
AJIB là hình bình hành nên 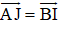
BCPQ là hình bình hành nên
CARS là hình bình hành nên
Do đó:
Bài 5 (trang 12 SGK Hình học 10):
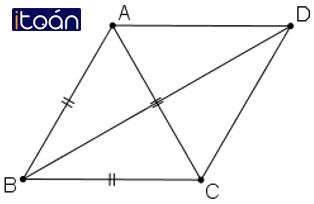
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ
Hướng dẫn giải:
Theo quy tắc hình bình hành với D là đỉnh còn lại của hình bình hành ABCD, ta có:
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
Lời kết
Sau khi học xong bài học Tổng và hiệu hai Vecto này, các em sẽ hiểu được Tổng và hiệu hai Vecto là gì và các cách tính. Nếu các em còn gặp khó khăn gì trong việc giải quyết bài tập hay cảm thấy phần lý thuyết còn khó hiểu, hãy nhắn tin ngay cho itoan để được giúp đỡ nhé. Chúc các em sức khỏe tốt và học tập thật giỏi nhé!
Xem thêm:
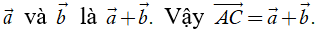
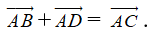
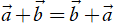 (tính chất giao hoán);
(tính chất giao hoán);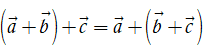 (tính chất kết hợp);
(tính chất kết hợp);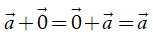 (tính chất của vectơ – không).
(tính chất của vectơ – không).