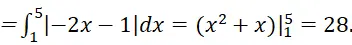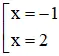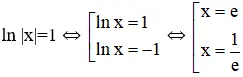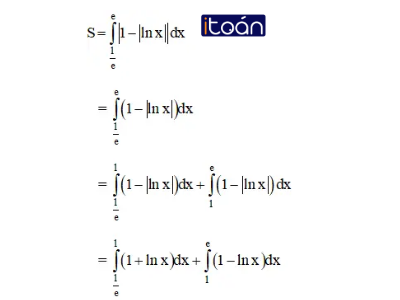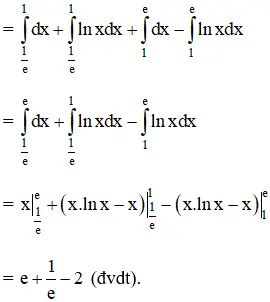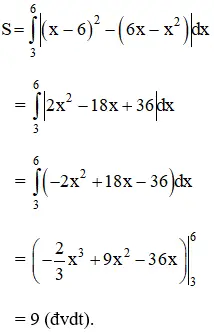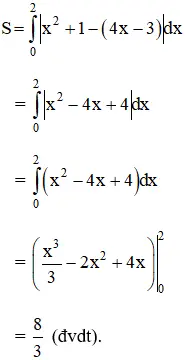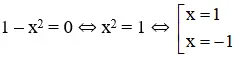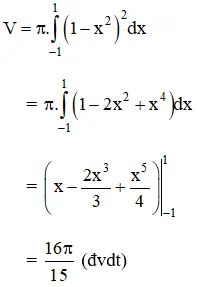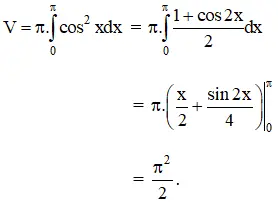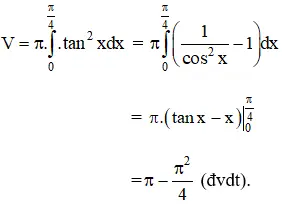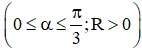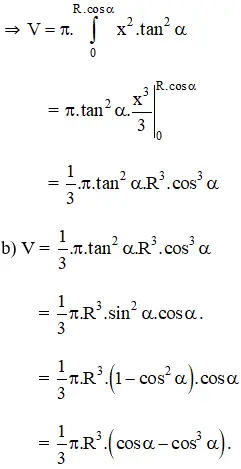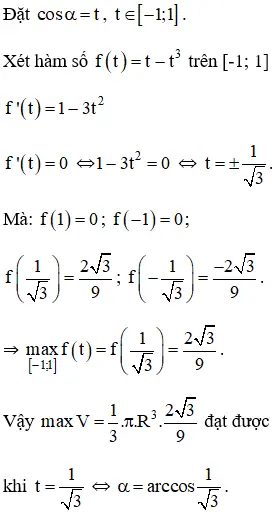Ứng dụng của tích phân trong hình học – Học tốt giải tích 12

Hôm nay chúng ta sẽ tiếp tục Series các bài giải hệ thống bài tập trong sách giáo khoa và sách bài tập Toán lớp 12. Itoan sẽ hỗ trợ các em tiết kiệm thời gian ôn luyện đạt hiệu quả nhất thông qua các phương pháp giải các dạng toán hay, nhanh và chính xác nhất. Dưới đây là lời giải bài tập SGK Bài 3 (Chương 3): Ứng dụng của tích phân trong hình học từ đội ngũ chuyên gia của itoan giàu kinh nghiệm biên soạn và chia sẻ.

Mục tiêu của bài học Ứng dụng của tích phân trong hình học

Kiến thức bài học hôm nay có đôi chút liên quan đến những bài học trước, các bạn cố gắng học tốt những bài học trước và đặt ra mục tiêu cụ thể cho bài học hôm nay nhé! 

•  Viết và giải thích được công thức diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục Ox, các đường thẳng x = a, x = b. Hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) và các đường thẳng x = a, x = b.
• Nắm được công thức thể tích của một vật thể nói chung.
• Nắm được công thức thể tích khối tròn xoay, công thức của khối nón, khối nón cụt, khối trụ tròn xoay trong trường hợp vật thể quay xung quanh trục Ox.
• Áp dụng được công thức tính diện tích hình phẳng, thiết lập được công thức tính thể tích khối chóp, khối nón và khối nón cụt.
• Ứng dụng được tích phân để tính được thể tích nói chung và thể tích khối tròn xoay nói riêng.
• Thấy được ứng dụng rộng rãi của tích phân trong việc tính diện tích, thể tích.

Lý thuyết bài học Ứng dụng của tích phân trong hình học

Dưới đây là một số phần kiến thức quan trọng cơ bản cô đã biên soạn cho bài học hôm nay, các bạn nhớ học bài kỹ trước khi làm bài tập nhé!

I. Tính diện tích hình phẳng

1. Diện tích hình phẳng giới hạn bởi một đường cong và trục hoành

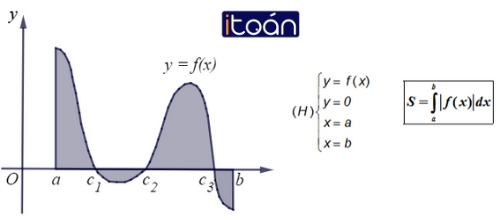
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a;b] , trục hoành và hai đường thẳng x=a,x=b được xác định: S=∫^b_a|f(x)|dx

Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=(x−2)²−1  , trục hoành và hai đường thẳng x=1,x=2.

Hướng dẫn giải:

Ta có: S=∫²₁ |(x−2)² − 1|dx=∫²₁|x²−4x+3|dx

Vì phương trình x²−4x+3 không có nghiệm trên 1;2  nên S=|∫²₁(x²−4x+3)dx|=2/3

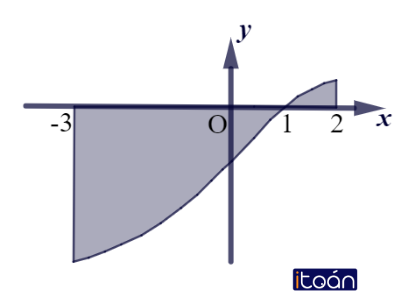
Ví dụ 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x) , trục hoành và hai đường thẳng x=−3,x=2. Đặt a=∫¹₋₃f(x)dx,b=∫²₁f(x)dx. Hãy tính S.

Hướng dẫn giải:

Ta có S=∫¹₋₃|f(x)|dx+∫²₁|f(x)|dx=−∫¹₋₃f(x)dx+∫²₁f(x)dx=−a+b

2. Hình phẳng giới hạn bởi 2 đường cong

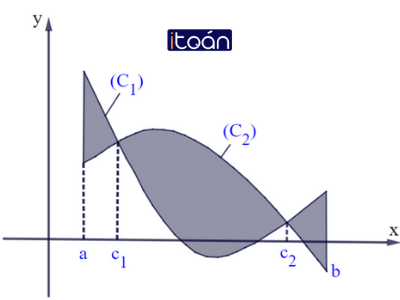
Diện tích hình phẳng (H) giới hạn bởi đồ thị hai hàm số (C1) y=f(x), (C2) y=g(x)  liên tục trên đoạn [a;b]  và hai đường thẳng  x=a,x=b (với a<b) được xác định theo công thức:  S=∫^b_a |f(x)−g(x)|dx

II. Tính thể tích

1.Thể tích của vật thể

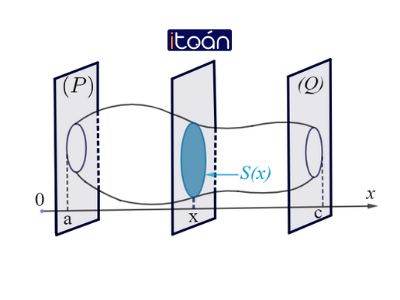
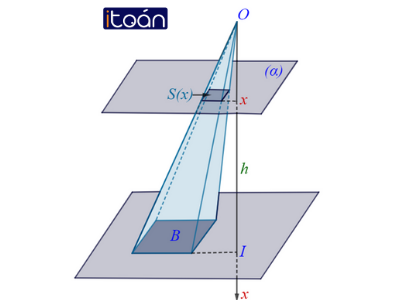
Cắt một vật thể B bởi hai mặt phẳng (P)  và (Q)  vuông góc với trục Ox lần lượt tại x=a  và x=b , với a<b . Một mặt phẳng tùy ý vuông góc với Ox tại điểm có hoành độ x (với a≤x≤b) cắt B theo thiết diện có diện tích S(x). Khi đó thể tích vật thể B là V=∫^b_a S(x)dx .

2. Thể tích khối chóp và khối chóp cụt

a. Thể tích khối chóp

Cho khối chóp có chiều cao bằng h và diện tích đáy bằng B. Chọn trục Ox vuông góc với mặt phẳng đáy tại điểm I sao cho gốc O trùng với đỉnh của khối chóp và có hướng xác định bởi vectơ OI. Khi đó OI=h. Một mặt phẳng (α) vuông góc với Ox tại x(0≤x≤h) cắt khối chóp theo thiết diện có diện tích là S(x).

Ta có:

b. Thể tích khối chóp cụt

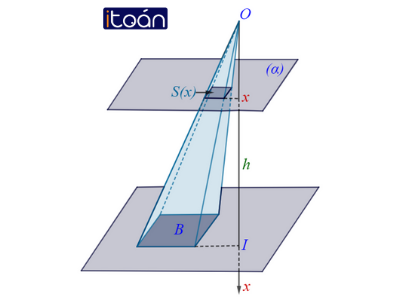
Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B,B′ và chiều cao bằng h.

Chọn trục Ox trùng với đường cao của khối chóp và gốc O trùng với đỉnh S. Hai mặt phẳng đáy của khối chóp cụt cắt Ox tại I và I′. Đặt OI=b,OI′=a(a<b). Gọi V là thể tích của khối chóp cụt.

Ta có:

III. Thể tích khối tròn xoay

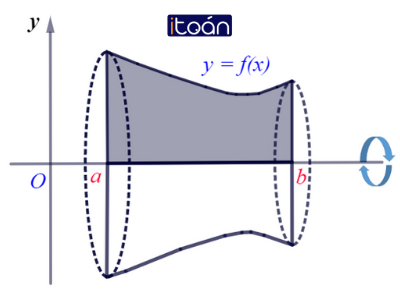
+ Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=a,x=b quanh trục Ox:

V = π∫^b_af²(x)dx

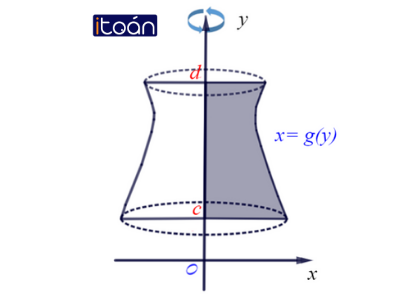
+ Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x=g(y), trục hoành và hai đường thẳng y=c,y=d quanh trục Oy là

V=∫^d_cg²(y)dx

Nếu sau khi học xong phần lý thuyết phía trên mà các bạn vẫn chưa hình dung ra cách làm bài thì đừng vội bỏ cuộc nhé, các bạn có thể tham khảo thêm bài giảng của Toppy qua đoạn video dưới đây để hiểu bài học hơn nhé!

Bài tập SGK Ứng dụng của tích phân trong hình học

Tiếp sau phần lý thuyết là phần giải các bài tập trong sách giáo khoa để áp dụng kiến thức vào bài tập nhé!

Trả lời câu hỏi Toán 12 Giải tích Bài 3 trang 114

Tính diện tích hình thang vuông được giới hạn các đường thẳng y = -2x – 1, y = 0, x = 1 và x = 5.

So sánh với diện tích hình thang vuông trong câu hỏi 1 bài 2.

Lời giải:

Ta có diện tích hình thang cần tính 

Công thức tính thể tích lăng trụ có diện tích đáy là B và chiều cao là h là: V = B*h.

– Khái niệm mặt tròn xoay: Trong không gian cho mặt phẳng (P) chứa đường thẳng Δ và chứ đường L. Khi quay mặt (P) xung quanh Δ một góc 360^o thì đường L tạo nên một mặt tròn xoay. Mặt tròn xoay đó nhận Δ làm trục, đường L được gọi là đường sinh.

– Khái niệm khối tròn xoay: Khối tròn xoay là khối hình học được tạo thành khi quay một hình phẳng quanh một đường thẳng cố định (trục quay) của hình.

Bài 1 (trang 121 SGK Giải tích 12): 

Tính diện tích hình phẳng giới hạn bởi các đường:

a) y = x²;y = x + 2

b) y =|lnx|; y = 1

c) y = (x – 6)²; y = 6x – x²

Lời giải:

a) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình :

x² = x + 2 ⇔ x² – x – 2 = 0 ⇔ 

Vậy diện tích cần tìm là:

b) Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:

Vậy diện tích cần tìm là:

(Vì lnx > 0 khi 1 < x < e và lnx < 0 khi

 ).

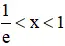
c) Hoành độ giao điểm của hai đồ thị là nghiệm của pt :

(x – 6)² = 6x – x²

⇔ (x – 6)(2x – 6) = 0

⇔ x = 3 hoặc x = 6

Vậy diện tích cần tìm là:

Bài 2 (trang 121 SGK Giải tích 12): 

Tính diện tích hình phẳng giới hạn bởi đường cong y = x²+1 , tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.

Lời giải:

Phương trình tiếp tuyến với đường cong y = x² + 1 tại điểm M(2; 5) là :

y = y’(2).(x – 2) + 5 ⇔ y = 4x – 3

Hoành độ giao điểm của tiếp tuyến và đường cong là x = 2.

Vậy diện tích hình giới hạn bởi y = x² + 1; tiếp tuyến y = 4x – 3; trục Oy (x = 0) và đường thẳng x = 2 là:

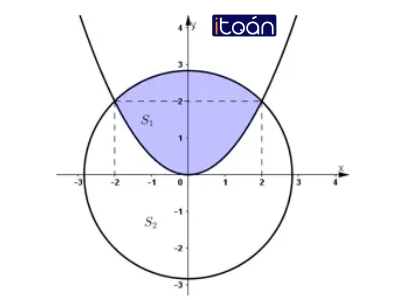
Bài 3 (trang 121 SGK Giải tích 12): 

Parabol 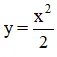 chia hình tròn có tâm tại gộc toạ độ, bán kính 2√2 thành hai phần. Tìm tỉ số diện tích của chúng.

Lời giải:

Bài 4 (trang 121 SGK Giải tích 12): 

Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:

Lời giải:

a) Hoành độ giao điểm là nghiệm của phương trình :

Vậy thể tích khối tròn xoay cần tính là:

b) Thể tích khối tròn xoay cần tính:

c) Thể tích khối tròn xoay cần tính:

Bài 5 (trang 121 SGK Giải tích 12): 

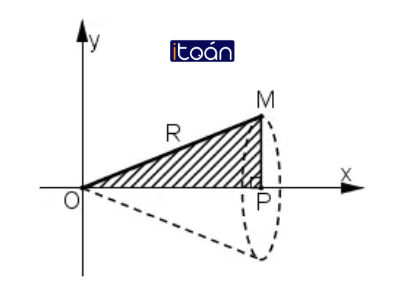
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt 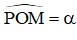 ; OM = R 

Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).

a) Tính thể tích của V theo α và R.

b) Tìm α sao cho thể tích V lớn nhất.

Lời giải:

a) OP = OM.sinα = R.cosα

Phương trình đường thẳng OM đi qua O nên có dạng: y = k.x

OM tạo với trục hoành Ox 1 góc

⇒ Hệ số góc k = tanα

⇒ OM: y = x.tanα

Vậy khối tròn xoay được tạo bởi hình phẳng giới hạn bởi đường thẳng y = x.tanα; y = 0; x = 0; x = R.cosα quay quanh trục Ox

Lời kết Ứng dụng của tích phân trong hình học

Vậy là bài giảng Ứng dụng của tích phân trong hình học của chúng ta sẽ khép lại tại đây, các bạn đã hiểu bài học chưa nhỉ? Cố gắng dành nhiều thời gian để tự ôn lại lý thuyết và làm bài tập nha! Ngoài bài học hôm nay, các bạn cũng có thể học tập nhiều bài học bổ ích khác nữa tại Toppy. Chúc các bạn học tập và áp dụng các kiến thức thật thành công.

Xem thêm bài giảng:

• Làm quen với số nguyên âm, tập hợp các số nguyên
• Số phần tử của một tập hợp, tập hợp con
• Phép nhân phân số
• Ghi số tự nhiên 
• Giải bài tập về ghi số tự nhiên