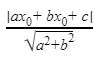Vị trí tương đối của đường thẳng và đường tròn – Học cùng Itoan

Với một chương mới về đường tròn ở hình học lớp 9, vị trí tương đối của đường thẳng và đường tròn là một kiến thức nền tảng vô cùng quan trọng để có thể áp dụng cho các bài tập sau này. Bài toán không chỉ ở những dạng lớp 9 mà còn xuyên suốt những năm học cấp 3 cùng với hình không gian và thi Đại học. Bài viết dưới đây, Itoan sẽ giúp các bạn hiểu kĩ hơn về phần lý thuyết này và một số bài tập liên quan.
Khái niệm về đường thẳng và đường tròn
Để có thể hiểu về các kiến thức sâu hơn, ta cần phải nắm chắc về những khái niệm cơ bản. Sau đây, Itoan sẽ giới thiệu cho các bạn những định nghĩa cơ bản nhất về đường thẳng và đường tròn trong hình học phẳng.
Đường thẳng
Đường thẳng là một khái niệm không được định nghĩa, là một cơ sở đầu tiên để xây dựng các khái niệm toán học khác. Đường thẳng có đặc điểm là không có chiều rộng và không cong tại mọi điểm. Một đường thẳng được xem là một đường dài, mỏng, thẳng và chỉ có một đường duy nhất đi qua hai điểm bất kì.
Đường tròn
Đường tròn là tập hợp của tất cả các điểm trên cùng một mặt phẳng. Và cách đều tâm (điểm cho trước) một khoảng cách nhất định. Đường tròn tâm O bán kính R được kí hiệu là (O;R).
Sau khi đã hiểu rõ các khái niệm về hai yếu tố chính của bài học toán 9 vị trí tương đối của đường thẳng và đường tròn. Itoan sẽ tiếp tục giới thiệu những kiến thức cơ bản của các vị trí tương đối.
Lý thuyết về ba loại vị trí tương đối giữa đường thẳng với đường tròn
Ba trường hợp về vị trí tương đối giữa đường thẳng với đường tròn là : Đường thẳng và đường tròn cắt nhau tại hai điểm . Đường thẳng và đường tròn tiếp xúc vuông góc tại một điểm duy nhất. Đường thẳng và đường tròn không giao nhau.
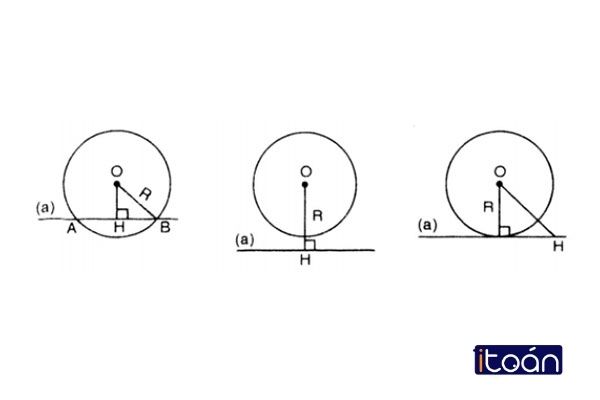
Đường thẳng và đường tròn cắt nhau
Đây là dạng đầu tiên của ba vị trí tương đối giữa đường thẳng với đường tròn. Trường hợp xảy ra khi một đường thẳng a bất kì cắt đường tròn tâm O bán kính R tại hai điểm chung.
Như vậy ta có thể nói, đường thẳng a và đường tròn (O;R) cắt nhau một khoảng từ O kẻ vuông góc với đường thẳng a. Gọi H là chân đường vuông góc và OH là khoảng cách giữa tâm và đường thẳng,
Đường thẳng và đường tròn tiếp xúc nhau tại một điểm
Trường hợp mà đường thẳng và đường tròn chỉ tiếp xúc tại 1 điểm chung duy nhất được gọi là điểm C. Thì ta có thể nói đường thẳng a và đường tròn (O;R) tiếp xúc với nhau.
Đường thẳng a trong trường hợp này được gọi là đường tiếp tuyến của đường tròn đó. Khoảng cách OC cũng được coi là bán kính của hình tròn (O;R).
Có một định lý cho trường hợp vị trí tương đối của đường thẳng và đường tròn này như sau: Nếu một đường thẳng a là đường tiếp tuyến của một đường tròn (O;R) thì đường thẳng đó vuông góc với bán kính R và tiếp xúc đường tròn tại tiếp điểm C.
Đường thẳng và đường tròn không tiếp xúc với nhau
Đây là trường hợp cuối cùng trong ba trường hợp vị trí tương đối giữa đường thẳng với đường tròn. Là khi mà giữa hai yếu tố đường thẳng và đường tròn không hề có một điểm chung nào.
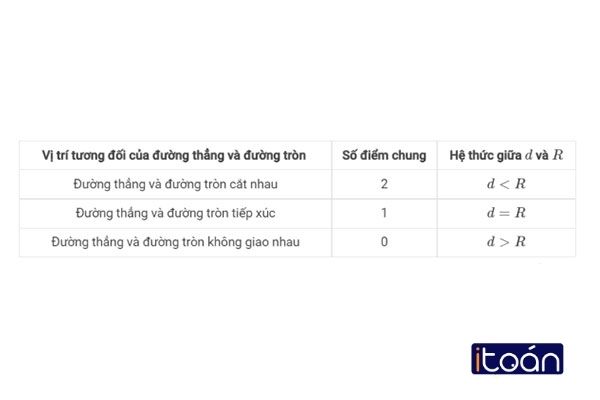
Hệ thức cho ba vị trí tương đối giữa đường thẳng và đường tròn
Từ các trường hợp như trên, có thể rút ra kiến thức trong bảng sau:
Các dạng bài tập thường gặp về vị trí tương đối giữa đường thẳng và đường tròn
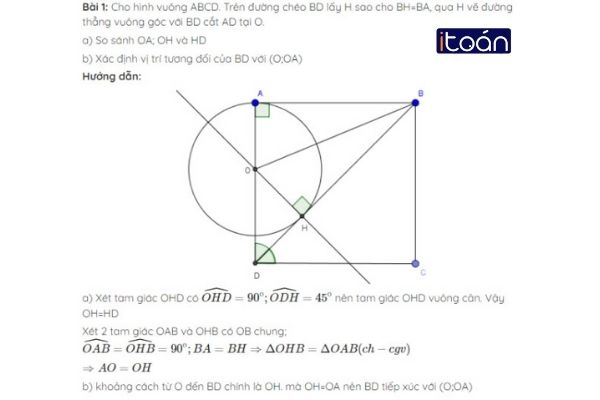
- Dạng 1: xác định vị trí tương đối giữa đường thẳng với đường tròn dựa vào hệ thức nêu trên. Từ đó, dựa vào tính chất của từng bài tập mà tính theo yêu cầu đề bài.
- Dạng 2: tính toán dựa vào tính chất tiếp tuyến. Đây là dạng bài tập thường gặp và có thể có dạng nâng cao. Khi gặp đề bài toán này, thường có một đường thẳng và là tiếp tuyến của đường tròn. Sau đó kẻ thêm hình và tính kết quả các cạnh. Thường áp dụng thêm định lý Py-ta-go.
- Dạng 3: Tìm tập hợp điểm cho sẵn theo yêu cầu đề bài. Dựa vào tính chất đường phân giác, đường vuông góc, đường song song để chứng minh.
Giải bài tập trong trục tọa độ:
Nếu cho một đường tròn (O;R) với R=d. Đường thẳng a chỉ tiếp xúc với đường tròn O khi khoảng cách từ O tới a bằng với bán kính R.
Trục tung Oy có phương trình x=0 nên đường tròn O tiếp xúc Oy khi và chỉ khi khoảng cách từ tâm O tới đường thẳng a bằng bán kính R.
Trục hoành Ox có phương trình y=0 nên đường tròn O tiếp xúc Ox khi và chỉ khi khoảng cách từ tâm O tới đường thẳng a bằng bán kính R.
Đường tròn O tiếp xúc cả 2 đường thẳng khi Ox=Oy=R.
Với đường thẳng a có dạng : ax + bx + c = 0 với tiếp điểm là C(x0;y0). Khoảng cách trong trục tọa độ được tính theo công thức :
Lời kết
Bài đọc Itoan đã khái quát cho bạn những kiến thức cơ bản để hình thành nên các trường hợp tương giao giữa đường thẳng và đường tròn. Từ khái niệm các đường cho tới đặc điểm các trường hợp. Mong rằng qua bài viết về vị trí tương đối của đường thẳng và đường tròn này sẽ giúp cho các bạn học sinh hiểu rõ hơn về bài học và làm tốt bài tập của mình. Chúc các bạn học tốt!