Bất phương trình bậc nhất một ẩn – Lý thuyết & Bài tập

Bất phương trình chứa một ẩn là kiến thức thuộc phần đại số của Toán 8. Trong bài viết sau Itoan sẽ giới thiệu về khái niệm bất phương trình bậc nhất một ẩn và tập nghiệm của bất phương trình. Hãy cùng Itoan khám phá ngay sau đây:
Thế nào là bất phương trình một ẩn?
Bất phương trình là gì?
Bất phương trình thường bao gồm những loại sau đây:
- Bất phương trình bậc nhất một ẩn. (trong đó, bất phương trình bậc nhất một ẩn lớp 8 là dạng toán đã xuất hiện trong chương trình học từ rất sớm).
- Bất phương trình bậc hai một ẩn.
- Bất phương trình bậc nhất hai ẩn.
Bất phương trình một ẩn là gì?
Khái niệm
Bất phương trình một ẩn là một mệnh đề so sánh giữa 2 hàm số f(x) và hàm số g(x) trên một trường số thực.
Việc giải tốt toán 8 bất phương trình bậc nhất một ẩn là tiền đề để tìm hiểu các bài toán về bất phương trình phức tạp hơn. Bất phương trình có chứa một ẩn thường được thể hiện dưới 1 trong các dạng sau:
- f(x) < g (x)
- f(x) > g(x)
- f(x) ≤ g(x)
- f(x) ≥ g(x)

Cách giải
Để tìm tập xác định của bất phương trình có một ẩn, ta cần phải tìm điểm giao giữa 2 tập xác định của 2 hàm số f(x) và g(x). Tất cả các bất phương trình một ẩn đều có thể được chuyển về dạng bất phương trình tương đương (điển hình như f(x) > 0, f(x) ≥ 0).
Trong bất phương trình 1 ẩn, biến x sẽ được gọi là ẩn. Như vậy, khi nhìn vào một bất phương trình f(x) > 0. Với giá trị x = a và f(a) > 0 là một bất đẳng thức đúng. Ta sẽ có: a là nghiệm của bất phương trình có một ẩn. Việc giải bất phương trình lớp 8 thành thạo sẽ giúp học sinh giải các loại bất phương trình phức tạp hơn.
Như Itoan đã đề cập, bạn có thể chuyển bất phương trình có chứa một ẩn về dạng f(x) > 0 hoặc f(x) ≥ 0. Khi phân loại bất phương trình có một ẩn nghĩa là phân loại bất phương trình theo hàm f(x).
- Những bất phương trình vô tỷ – bất phương trình khai căn.
- Bất phương trình mũ là những bất phương trình mà trên lũy thừa có chứa biến hay còn được gọi là bất phương trình có hàm mũ.
- Bất phương trình logarit là những bất phương trình có chứa biến bên trong dấu logarit.
- Bất phương trình bậc k là những bất phương trình chứa f(x) là một đa thức bậc k.
Bất phương trình bậc nhất một ẩn
Bất phương trình bậc nhất 1 ẩn là một loại thuộc các phương trình 1 ẩn. Bất phương trình bậc nhất có một ẩn thường được viết dưới dạng sau đây:
- ax + b < 0
- ax + b > 0
- ax + b 0
- ax + b 0
Trong dạng bất phương trình này, a và b là 2 số đã được cho trước và a ≠ 0.
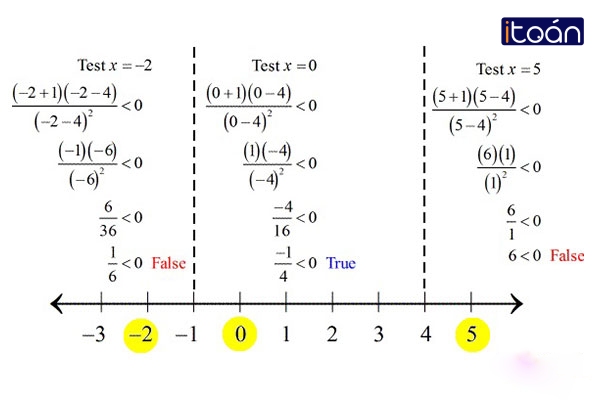
Giải bất phương trình bậc nhất một ẩn
Những quy tắc khi biến đổi bất phương trình
Để biến đổi BPT bậc nhất 1 ẩn, bạn cần phải thực hiện theo 2 quy tắc quan trọng là quy tắc chuyển vế hoặc quy tắc nhân với một số.
Quy tắc chuyển vế
Quy tắc chuyển vế được phát biểu rất đơn giản, khi bạn chuyển một hạng tử trong bất phương trình từ một vế sang vế còn lại, bạn cần phải đổi dấu của hạng tử đó.
Quy tắc nhân với một số
Quy tắc nhân với một số nghĩa là bạn nhân 2 vế của bất phương trình bậc nhất có một ẩn với cùng một số khác 0. Khi đó, bạn cần phải.
- Giữ nguyên chiều của bất phương trình như cũ nếu số được nhân là số dương.
- Đổi chiều của bất phương trình sang chiều ngược lại nếu số được nhân là số âm.
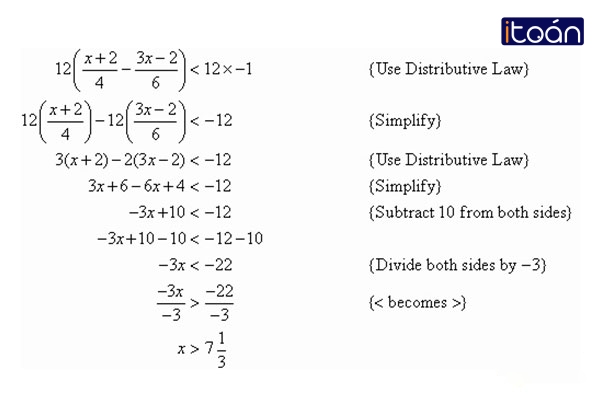
Áp dụng giải bất phương trình bậc nhất một ẩn
Sau khi đã áp dụng 2 quy tắc chuyển vế và quy tắc nhân với một số vào các vế của bất phương trình, các bạn có thể bắt đầu giải BPT bậc nhất 1 ẩn như sau: Bất phương trình có dạng ax + b > 0 ⇒ ax > -b.
- Nếu a > 0 thì bất phương trình sẽ có nghiệm là x > -b/a.
- Nếu a < 0 thì bất phương trình sẽ có nghiệm là x < b/a.
Như vậy, bài viết trên đã tổng hợp tất cả những kiến thức liên quan đến bất phương trình, bất phương trình bậc nhất một ẩn cũng như hướng dẫn giải những dạng bất phương trình.
>> Xem thêm: Giải bài toán bằng cách lập phương trình – Học tốt toán lớp 8
