Góc tạo bởi tia tiếp tuyến và dây cung – Toán học dễ dàng cùng itoan

Góc tạo bởi tia tiếp tuyến và dây cung trong đường tròn là một trong những góc đặc biệt là thường bắt gặp trong những bài toán khó lớp 9. Để có thể nắm vững được kiến thức và các mẹo nâng cao điểm Toán của loại góc đặc biệt này cũng như các dạng bài tập thường gặp. Hãy cùng itoan tìm hiểu chi tiết qua bài giảng ngay sau đây.
I. Lý thuyết của góc tạo bởi tia tiếp tuyến và dây cung
1. Định nghĩa
Được định nghĩa như sau:
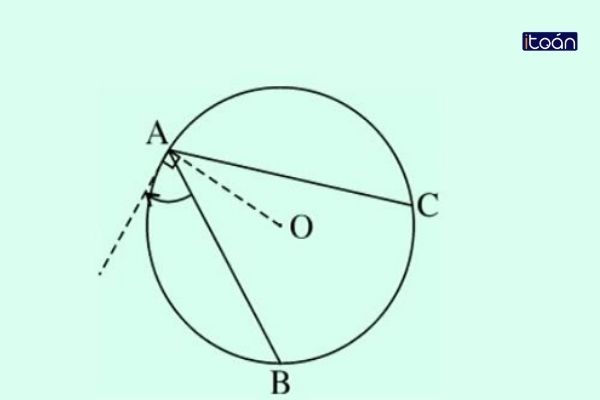
- Xét đường tròn tâm O, bán kính R (O;R) ta có đỉnh A của góc BAx nằm trên đường tròn và cạnh Ax là tia tiếp tuyến, cạnh còn lại chứa dây cung AB. Khi đó ta có góc BAx chính là góc được tạo bởi dây cung và tia tiếp tuyến.
2. Định lí:
Góc giữa tiếp tuyến và dây cung có số đo bằng một nửa số đo cung bị chắn.
3. Hệ quả:
Góc được tạo bởi dây cung và tia tiếp tuyến trong 1 đường tròn và góc nội tiếp mà cùng chắn 1 cung sẽ có số đo bằng nhau.
II. Các dạng bài tập
Qua bài giảng lý thuyết về toán 9 bài 4, các em cần hoàn thành được 1 số mục tiêu mà bài giảng đưa ra như:
- Nắm vững được định nghĩa, định lí và các hệ quả
- Vận dụng được các lý thuyết và giải được các bài tập tự luận cơ bản và trong sách giáo khoa.
1. Bài tập tự luận
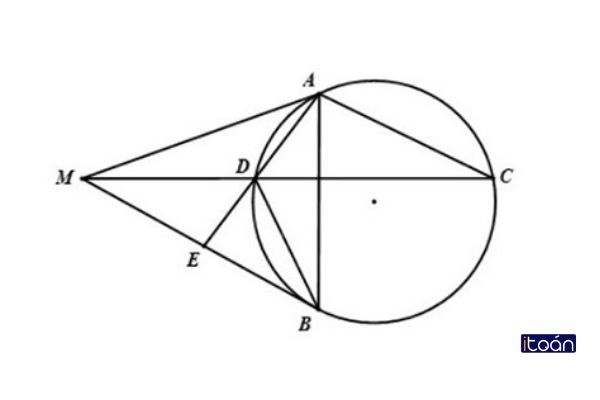
Bài tập 1: Cho đường tròn tâm O, bán kính R, từ điểm nằm ngoài đường tròn M, vẽ 2 tiếp tuyến lần lượt là MA và MB của đường tròn tâm O và cắt tại điểm A, B. Qua điểm A vẽ một đường thẳng song song với tiếp tuyến MB và cắt đường tròn tại điểm C. Nối điểm C với M và cắt đường tròn tâm O tại điểm D. Nối điểm A với D và cắt tiếp tuyến MB tại điểm E. Chứng minh:
- a) ΔABE và ΔBDE là 2 tam giác đồng dạng. ΔMEA và ΔDEM là 2 tam giác đồng dạng.
- b) Điểm E là trung điểm của đường tiếp tuyến MB.
Hướng dẫn giải:
-
a) Xét ΔABE và ΔBDE ta có:
- E là góc chung
- Góc BAE = Góc DBE (Là góc nội tiếp và là góc được tạo bởi dây cung và tia tt cùng chắn 1 cung BD).
Vậy ΔABE và ΔBDE là 2 tam giác đồng dạng theo trường hợp góc góc.
Ta có AC // MB ⇒ Góc ACM = Góc CMB (2 góc so le trong)
Mà ta có ACM = MAE (2 góc nội tiếp và là góc nằm giữa dây cung và tia tiếp tuyến cùng chắn cung AD)
⇒ Góc CMB = Góc MAE
Xét ΔMEA và ΔDEM ta có:
- E là góc chung
- Góc MAE = Góc CMD (cmt)
Vậy ΔMEA và ΔDEM là 2 tam giác đồng dạng theo trường hợp góc góc.
-
b) Ta có:
- ΔABE và ΔBDE là 2 tam giác đồng dạng ⇒ 2EB = AE.DE
- ΔMEA và ΔDEM là 2 tam giác đồng dạng ⇒ 2ME = DE.EA
Vậy EB = EM ⇒ E là trung điểm của đường tiếp tuyến MB.
2. Bài tập sách giáo khoa:
Đây là kiến thức vô cùng quan trọng theo sát các em về sau. Chính vì vậy dưới đây là một số bài toán về kiến thức này trong sách giáo khoa để các bạn ôn luyện được hiệu quả.
Bài tập 1 (Bài 28/SGK trang 79 Toán 9, Tập 2)
Cho 2 đường tròn tâm (O), (O’) và cắt nhau tại 2 điểm lần lượt là A và B. Tiếp tuyến từ điểm A của đường tròn tâm (O) tại điểm P. Tia PB sẽ cắt đường tròn tâm (O’) tại Q. Chứng minh rằng đường thẳng AQ là đường thẳng song song tiếp tuyến tại điểm P của đường tròn tâm (O) dựa vào các định lý của góc tạo bởi tia tiếp tuyến và dây cung.
Bài tập 2 (Bài 29/SGK trang 79 Toán 9, Tập 2)
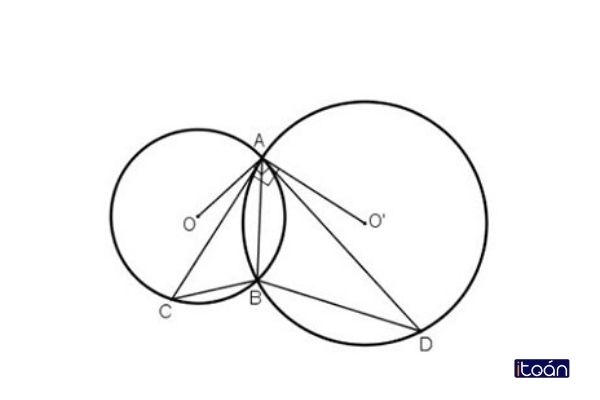
Cho 2 đường tròn tâm (O), (O’) và cắt nhau tại 2 điểm lần lượt là A và B. Tiếp tuyến từ điểm A của đường tròn tâm (O’) cắt đường tròn tâm (O) tại điểm C và đường tròn tâm (O) cắt đường tròn tâm (O’) tại điểm D. Chứng minh góc CBA = góc DBA
Bài tập 3 (Bài 30/SGK trang 79 Toán 9, Tập 2)
Sử dụng định lý đảo. Nếu như góc BAx bằng nửa số đo cung AB và đây là cung nằm bên trong của góc đó thì cạnh Ax sẽ là tia tiếp tuyến đường tròn. (Gợi ý có thể chứng minh bằng phương pháp phản chứng hoặc phương pháp trực tiếp của góc tạo bởi tia tiếp tuyến và dây cung)
Bài giảng trên đã cung cấp kiến thức về góc tạo bởi tia tiếp tuyến và dây cung cũng như các dạng bài tập và hướng dẫn chi tiết. Hy vọng đây sẽ là những kiến thức bổ ích dành cho các bạn học sinh ôn luyện được hiệu quả. Nếu có nhu cầu tìm kiếm thêm những kiến thức toán lớp 9 hoặc có bất kỳ câu hỏi liên quan hãy liên hệ với Itoan để được giải đáp nhanh nhất có thể.