Phép đối xứng tâm Toán 8 – Tổng hợp lý thuyết & bài tập

Một trong những bài học các em không thể bỏ qua trong Toán học lớp 8 chính là bài học về phép đối xứng tâm. Bài học này, Itoan sẽ giới thiệu đến các em phần lý thuyết chung và phần thực hành liên quan đến phép đối xứng tâm. Cùng Itoan, tìm hiểu ngay sau đây:
Lý thuyết
Định nghĩa
Trong lý thuyết về đối xứng tâm lớp 8, việc đưa ra định nghĩa phép đối xứng tâm thông qua việc định nghĩa các phép đối xứng về điểm, hình đối xứng hay hình có tâm đối xứng. Hiểu đơn giản nếu phép biến hình biến M thành M’ sao cho:
- I là trung điểm của đoạn thẳng MM’ thì được gọi là phép đối xứng tâm I.
- Trong trường hợp M trùng với I thì biến hình đối xứng tâm sẽ biến I thành chính nó.
Vì là một phép dời hình, nên tất cả tính chất của phép dời hình cũng có ở trong phép này. Nếu I là tâm của hình. H chính là đối xứng qua tâm của H cũng chính là H. Hay như M’ là ảnh qua phép đối xứng tâm I của M. Chứng tỏ M là ảnh của M’ của phép biến hình đối xứng tâm I và ngược lại.
Hai điểm đối xứng qua một điểm
Trước tiên, lý thuyết các em cần phải hiểu đó chính là hai điểm đối xứng qua một điểm. Nó được gọi là đối xứng nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Quy ước: Điểm đối xứng với O qua điểm O cũng là O.
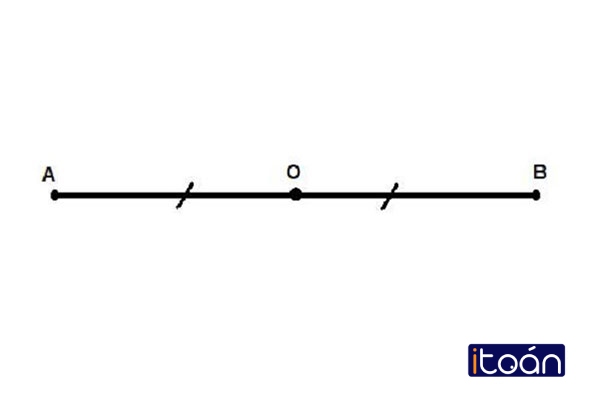
Hai điểm A và A’ đối xứng nhau qua điểm O. Như vậy. A, O và A’ thẳng hàng và OA’=OA.
Hai hình đối xứng qua một điểm
Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm của hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.
Như vậy, nếu xét các điểm A, B, C đối xứng qua O
=> A’, B’, C’ là các đỉnh của hình tam giác.
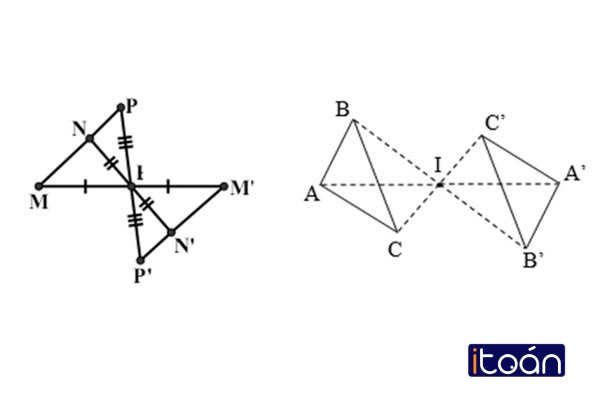
Từ định nghĩa trên, ta thấy nếu hai hình đối xứng qua một điểm thì các điểm (ví dụ A, B) sẽ có đầy đủ tính chất:
- AB = A’B’
- AB và A’B’ đối xứng với nhau qua O.
Một điểm đáng lưu ý trong đối xứng tâm toán 8 chính là:
- Hình đối xứng của đường tròn là đường tròn bằng nó.
- Hình đối xứng của của một đường thẳng là đường thẳng song song với nó,
- Hình đối xứng của của một góc là một góc bằng nó.
- Hình đối xứng của một tam giác cũng là một tam giác bằng nó.
Hình có tâm đối xứng
Nhìn vào thực tế, chúng ta sẽ thấy một vài hình có tâm đối xứng vô cùng quen thuộc trong đời sống hằng ngày. Ví dụ như đường tròn (tâm đối xứng chính là tâm của nó); hình bình hành (tâm đối xứng là giao điểm của hai đường chéo). Như vậy, giao điểm của hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Tóm lại, điểm O được gọi là tâm đối xứng của hình H nếu điểm đối xứng của mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
Như vậy, phép đối xứng tâm qua mỗi hình, mỗi điểm sẽ được định nghĩa khác nhau. Bên cạnh những định nghĩa trên, các em còn được tiếp xúc với khái niệm tâm đối xứng của đồ thị hàm số trong những bài học ở lớp cao hơn.
Các dạng bài toán về phép đối xứng tâm
Từ lý thuyết ở trên, có rất nhiều dạng bài tập khác nhau áp dụng phép biến hình này. Các em có thể thấy các dạng bài sau nhé.
- Dạng 1: Xác định ảnh của một hình. Để giải được bài toán này, các em phải sử dụng đến biểu thức tọa độ và tính chất của nó để áp dụng giải.

- Dạng 2: Xác định tâm đối xứng khi biết ảnh và tạo ảnh.
- Dạng 3: Tìm tâm đối xứng của một hình. Ở dạng bài này, sử dụng định nghĩa và tính chất của hình có tâm đối xứng để giải;
- Dạng 4: Sử dụng phép biến hình đối xứng tâm để giải bài toán dựng hình.
- Dạng 5: Giải bài toán hợp điểm.
Có tới 5 dạng bài áp dụng để giải các phép biến hình đối xứng tâm. Vì thế, phần lý thuyết vô cùng quan trọng để giúp cho các em có thể áp dụng vào từng bài một cách nhuần nhuyễn.
Như vậy, chúng ta đã cùng nhau trải qua các lý thuyết cần nắm vững và các dạng bài tập thực hành cho nội dung phép đối xứng tâm. Chúc các em thành công và giải những bài toán tương tự một cách thuần thục.
>> Xem thêm: Phép đối xứng trục – Chinh phục Toán 8 Hình học
