Phép tịnh tiến – Học toán 11

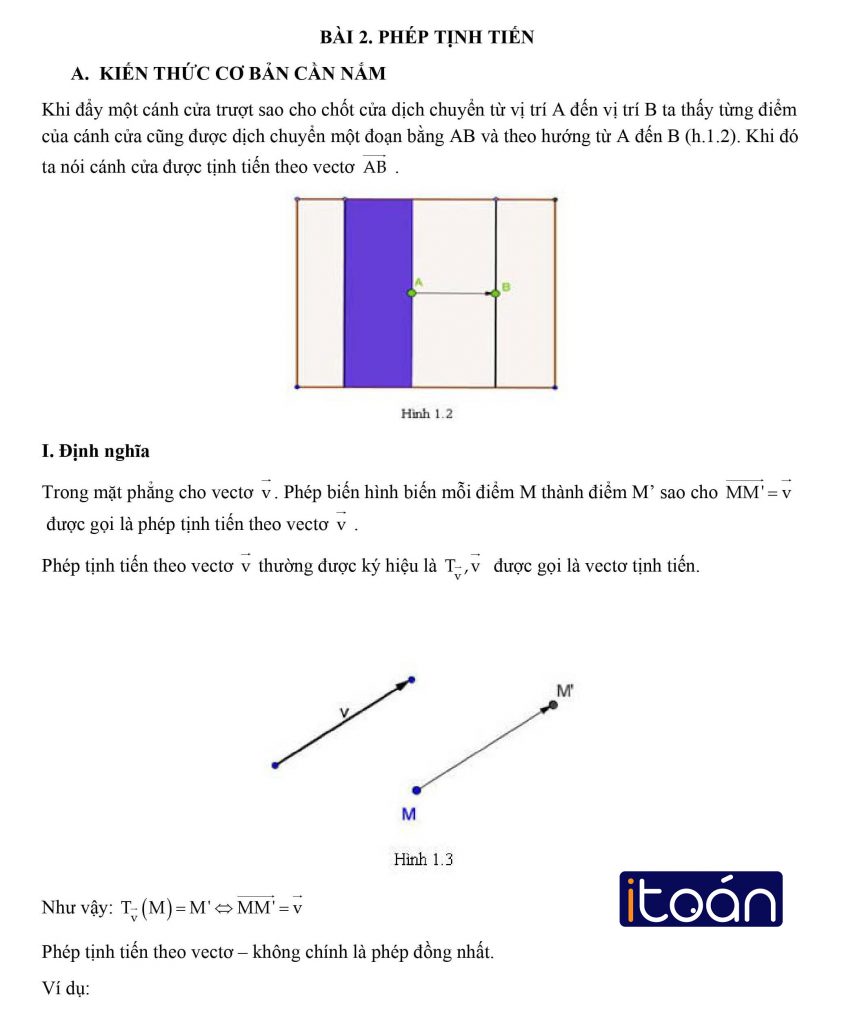
Ở bài học trước , chúng ta đã cùng nhau làm quen với phép biến hình đầu tiên , các bạn còn nhớ đó là phép gì không nhỉ ? Nếu chưa nhớ ra hãy qua lại bài học hôm qua và tiếp tục bài học này nhé .Bài học hôm nay sẽ giới thiệu thêm một phép dời hình nữa . Các bạn có đoán ra được phép đó mang tên gì không ? Vậy thì để Itoan bật mí cho bạn , đó chính là” phép tịnh tiến ” – một phép toán hình học quan trọng.
Cùng đi khám phá xem sự thú vị của bài học : Phép tịnh tiến!
Mục tiêu bài học : Phép tịnh tiến
Qua bài học hôm nay các bạn sẽ học được :
- Định nghĩa , tính chất của phép tịnh tiến
- Các tịnh tiến và áp dụng vào làm các bài tập từ cơ bản đến nâng cao
Kiến thức cần nhớ của bài học : Phép tịnh tiến
Sau đây là một số nội dung quan trọng của bài học , các bạn chú ý ghi chép lại những kiến thức cốt lõi để hiểu và áp dụng làm bài tập
Hướng dẫn giải bài tập SGK Toán 11 bài học : Phép tịnh tiến
Bài học trên đã giúp các bạn hiểu được phần nào về bài học của chúng ta .Vậy hãy cùng giải một số bài tập trong SGK nhé !
Bài 1 (trang 7 SGK Hình học 11)
![]()
Lời giải:
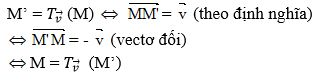
Bài 2 (trang 7 SGK Hình học 11)
Ta có bài toán như sau : Cho tam giác ABC có G là trọng tâm. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ AG . Dựng điểm D sao cho phép tịnh tiến theo vectơ AG biến D thành A.
Lời giải:
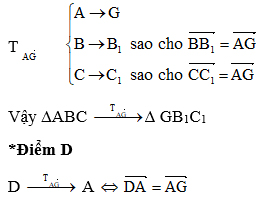
<=> A là trung điểm của đoạn thẳng DG
Bài 3 (trang 7 SGK Hình học 11)
Bài toán cung cấp cho chúng ta những dữ liệu sau : Trong mặt phẳng tọa độ Oxy cho vectơ v→ = (-1; 2), A(3; 5), B(-1; 1) và đường thẳng d có phương trình x – 2y + 3 = 0.
a. Tìm tọa độ của các điểm A’, B’ theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v.
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v→.
c. Tìm phương trình của đường thẳng d’ là ảnh của d qua phép tịnh tiến theo v.
Lời giải:
a. Gọi tọa độ của A’ là (x’, y’). Theo công thức tọa độ của phép tịnh tiến, ta có:
vecto v = (-1; 2), A(3; 5); A’ = Tv.(A) => x’ = – 1 + 3 => x’ = 2
y’ = 2 + 5 => y’ = 7 => A’(2, 7)
Tương tự, ta tính được B’(-2 ; 3).
b. Gọi tọa độ của C là (x; y). A(3; 5) là ảnh của C qua phép tịnh tiến theo vectơ
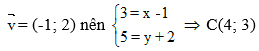
c. Vì d’ = Tv.(d) nên d’ // d, do đó để viết phương trình của d’, ta tìm một điểm M ∈ d và ảnh M’ của nó qua phép tịnh tiến theo vectơ v→ và sau đó viết phương trình đường thẳng đi qua M’ và song song với d.
Trong phương trình x – 2y + 3 = 0, cho y = 0 thì x = – 3. Vậy ta được điểm M(-3; 0) thuộc d.
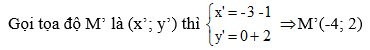
Đường thẳng d có phương trình: x – 2y + 3 = 0
Đường thẳng d’ song song với d có phương trình x – 2y + m =0, d’ đi qua M’ nên:
(-4) – 2.2 + m = 0 <=> m = 8.
Vậy phương trình của d’ là: x – 2y + 8 = 0
Bài 4 (trang 8 SGK Hình học 11)
Bài toán có những dữ liệu sau :Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Lời giải:
*Lấy A ∈ a và B ∈ b, lúc đó:
Phép tịnh tiến vectơ AB biến a thành b.
*Vì có vô số cách chọn A ∈ a và B ∈ b nên có vô số phép tịnh tiến biến a thành b.
Một số bài tập củng cố kiến thức : Phép tịnh tiến
Cùng luyện tập thêm với một số bài tập dưới đây nhé !
Lời kết :
Bài học của chúng ta đã kết thúc , Itoan mong rằng các bạn có thể áp dụng các kiến thức đã được học ở trên để làm được những dạng bài toán liên quan .Với các kiến thức trọng tâm kết hợp với các ví dụ minh học dễ hiểu sẽ giúp các bạn tư duy các bài toán tốt hơn. Các bạn cần chăm chỉ xem lại bài và hoàn thiện các bài tập để củng cố lại kiến thức .Các bạn có thể tham khảo những bài giảng hay khác tại : https://www.toppy.vn/
Chúc các bạn học tốt !
Xem thêm :
- 6 cộng với một số: 6+5 – Bài tập & Lời giải Toán lớp 2
- Phép cộng 25+14- SGK Lớp 1 Cánh diều
- Phép cộng dạng 14+3- SGK Toán 1