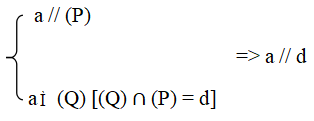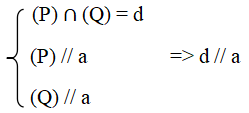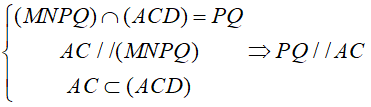Đường thẳng và mặt phẳng song song – Học tốt toán 11

Sau khi đã cùng nhau đi tìm hiểu những phép dời hình trong toán học lớp 11 thì chúng ta sẽ được tìm hiểu những mối quan hệ , tính chất của đường thẳng và mặt phẳng . Bài học “ Đường thẳng và mặt phẳng song song ” sẽ giúp bạn giải đáp toàn bộ thắc mắc về nội dung kiến thức của bài học . Cùng bước vào bài học ngay nhé các bạn.
Mục tiêu bài học : Đường thẳng và mặt phẳng song song
Sau bài học , các bạn cần nắm bắt được những kiến thức sau :
- Mối liên hệ giữa đường thẳng và mặt phẳng
- Các dạng bài tập đặc trưng và phương pháp giải
- Hoàn thiện các bài tập luyện tập
Kiến thức cơ bản của bài học : Đường thẳng và mặt phẳng song song
Dưới đây là toàn bộ kiến thức cần nhớ của bài học : Đường thẳng và mặt phẳng
1. Vị trí tương đối của đường thẳng và mặt phẳng
Cho đường thẳng a và mặt phẳng (P). Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:
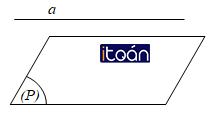
a. Đường thẳng a và mặt phẳng (P) không có điểm chung, tức là:
a ⋂ (P) = ∅ ⇔ a // (P).
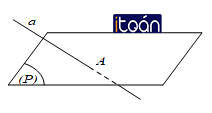
b. Đường thẳng a và mặt phẳng (P) chỉ có một điểm chung, tức là:
a ⋂ (P) = A ⇔ a cắt (P) tại A.
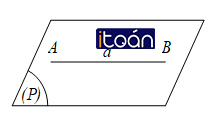
c. Đường thẳng a và mặt phẳng (P) có hai điểm chung, tức là:
Ta có :a ⋂ (P) = {A, B} ⇔ a ∈ (P).
Ta có tính chất như sau :a ⋂ (P) = ∅ ⇔ a // (P).
Ta có tính chất như sau : a ⋂ (P) = A ⇔ a cắt (P)
Ta có tính chất như sau : a ⋂ (P) = {A, B} ⇔ a ∈ (P).
2. Điều kiện để một đường thẳng song song với một mặt phẳng
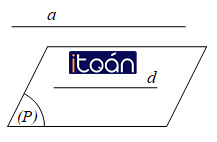
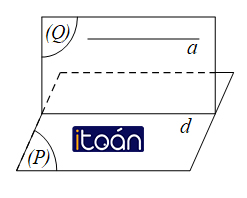
Định lí 1: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).
Tức là, a ∉ (P) thì nếu: a // d ∈ (P) ⇒ a // (P).
3. Tính chất
Định lí 2 được phát biểu như sau : Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì sẽ cắt theo một giao tuyến song song với a.
Tức là, nếu
Hệ quả 1 được phát biểu như sau : Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng.
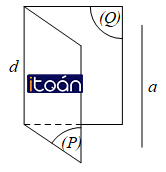
Hệ quả 2 được phát biểu như sau : Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến (nếu có) của chúng song song với đường thẳng đó.
Tức là:
Hệ quả 3 được phát biểu như sau : Nếu a và b là hai đường thẳng chéo nhau thì qua a có một và chỉ một mặt phẳng song song với b.
Hướng dẫn giải bài tập SGK Toán lớp 11 bài học : Đường thẳng và mặt phẳng song song
Sau đây để luyện tập thêm về kiến thức đã học ở trên , chúng ta sẽ cùng nhau đi làm một số bài tập cơ bản SGK nhé !
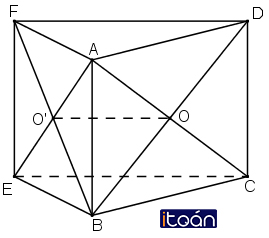
Bài 1 : Ta có đề bài như sau :Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song và các mặt phẳng (ADF) và (BCF)
b) Gọi M và N lần lượt là trọng tâm của tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).
Lời giải:
a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO’ // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ Ta có kết luận về bài toán : OO’ // (BCE).
b)
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên ta có thể kết luận MN // (CEFD) hay MN // (CEF).
Bài 2 :
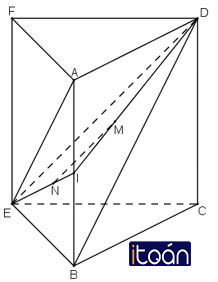
Bài tập của chúng ta như sau : Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường thẳng AC và BD.
a) Tìm giao tuyến của (α) với các mặt của tứ diện.
b) Thiết diện của tứ diện cắt bởi mặt phẳng (α) là hình gì?
Lời giải:
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.
Bài 3 :
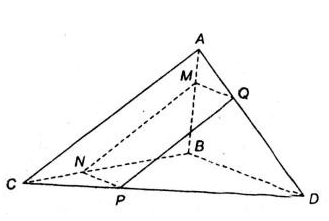
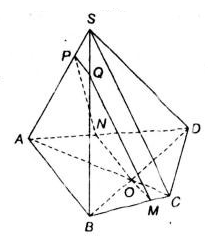
Đề bài của chúng ta như sau : Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
Lời giải:
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.
Lời kết :
Bài học sẽ ngày càng dài , kiến thức ngày càng khó ,chính vì vậy mà các bạn cần phải cố gắng ,nỗ lực hết mình để hiểu và áp dụng vào làm các bài tập liên quan . Một yếu tố qua trọng bên cạnh những bài giảng hay đó chính là ý thức của các bạn , tinh thần tự học cao sẽ giúp các bạn học tập tốt .Itoan mong rằng sẽ có thể đồng hành với các bạn , giúp cho các bạn học tập tốt hơn . Các bạn có thể tham khảo thêm các bài giảng khác tại : https://www.toppy.vn/
Chúc các bạn học tập tốt !
Xem thêm :
- Khoảng cách – Hướng dẫn học tốt Hình học lớp 11 – itoan
- Hai đường thẳng song song
- Hai đường thẳng chéo nhau và hai đường thẳng song song
- Từ vuông góc đến song song