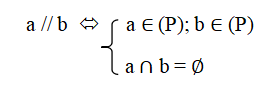Hai đường thẳng chéo nhau và hai đường thẳng song song – Toán 11

Sau đây , bài học mang tên : ” Hai đường thẳng chéo nhau và hai đường thẳng song song “.Đề bài cũng đã phần nào tiết lộ cho các bạn về bài học của chúng ta về những vấn đề sẽ được giải quyết trong bài học rồi phải không ? Nhưng để hiểu sâu và áp dụng vào làm các bài tập vẫn dụng thì các bạn cần phải chú ý ,tập trung học lý thuyết và làm bài tập thực hành . Bạn không cần tìm kiến đâu xa vì Itoan đã soạn ra một bài giảng về chủ đề này . Chúng ta cùng bước vào bài học ngay nhé !
Mục tiêu bài học : Hai đường thẳng chéo nhau và hai đường thẳng song song
Sau đây là tóm tắt những nội dung mà các bạn sẽ học trong bài :
- Vị trí tương đối của hai đường thẳng
- Hai đường thẳng song song
- Hoàn thiện bài tập cơ bản trong SGK
Kiến thức cơ bản của bài học : Hai đường thẳng chéo nhau và hai đường thẳng song song
Sau đây là toàn bộ kiến thức cơ bản của bài học
1. Vị trí tương đối của hai đường thẳng phân biệt
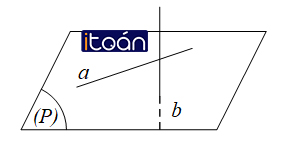
Cho hai đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của hai đường thẳng ta có bốn trường hợp sau:
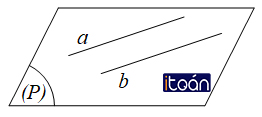
a. Hai đường thẳng song song: cùng nằm trong một mặt phẳng và không có điểm chung, tức là
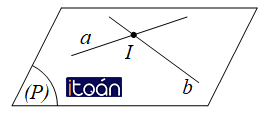
b. Hai đường thẳng cắt nhau: chỉ có một điểm chung.
a cắt b khi và chỉ khi a ⋂ b = I.
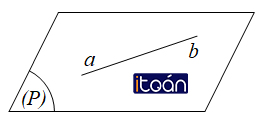
c. Hai đường thẳng trùng nhau: có hai điểm chung phân biệt.
a ⋂ b = {A, B} ⇔ A ≡ B
d. Hai đường thẳng chéo nhau: không cùng thuộc một mặt phẳng.
a chéo b khi và chỉ khi a, b không đồng phẳng.
a song song với b
a cắt b tại giao điểm I
a và b cắt nhau tại vô số điểm (trùng)
a và b chéo nhau
2. Hai đường thẳng song song
Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.
Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Định lí: (về giao tuyến của hai mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Hệ quả: Nếu hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).
Hướng dẫn giải bài tập toán SGK lớp 11 bài học : Hai đường thẳng chéo nhau và hai đường thẳng song song
Học thì nên đi đôi với hành .Nắm được nguyên tắc như vậy thì sau khi học xong lý thuyết chúng ta nên bắt tay ngay vào làm những bài tập cơ bản củng cố kiến thức . Sau đây cùng Itoan đi giải bài tập trong SGK nhé !
Bài 1 :
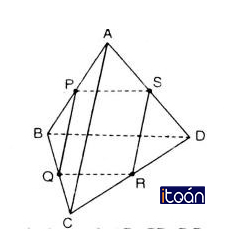
Sau đây là đề bài của bài toán cần ta giải : Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD và DA. Chứng minh rằng nếu bốn điểm P, Q, R và S đồng phẳng thì:
a) Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy.
b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy.
Lời giải:
a) Ta có:
PQ = (ABC) ∩ (PQRS)
RS = (PQRS) ∩ (ACD)
AC = (ABC) ∩ (ACD)
Vậy hoặc PQ, RS, AC đồng qui hoặc song song.
b) PS =(ABD) ∩ (PQRS)
RQ = (BCD) ∩ (PQRS)
BD = (ABD) ∩ (CBD)
Vậy PS, RQ, BD đồng quy hoặc song song.
Bài 2 :
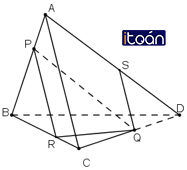
Đề bài cho ta những dữ liệu sau đây : Cho tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.
a) PR song song với AC;
b) PR cắt AC.
Lời giải:
a) PR // AC
mp(PQR) và mp(ACD) lần lượt chứa hai đường thẳng song song PR // AC
⇒ (PQR) ∩ (ACD) = Qt là đường thẳng song song với AC và PR.
Gọi Qt ∩ AD = S
⇒ S = AD ∩ (PQR).
b) PR ∩ AC = I.
Có : Q ∈ (ACD) ∩ (PQR)
+ (ABC) ∩ (PQR) = PR.
+ (ACD) ∩ (ABC) = AC
+ (ACD) cắt (PQR)
⇒ PR; AC và giao tuyến của (ACD) và (PQR) đồng quy
Mà PR ∩ AC = I
⇒ I ∈ (ACD) ∩ (PQR).
⇒ (ACD) ∩ (PQR) = QI.
trong (ACD): QI ∩ AD = S chính là giao tuyến của (PQR) và AD.
Bài 3 :
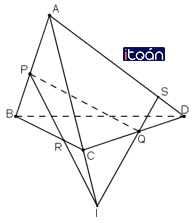
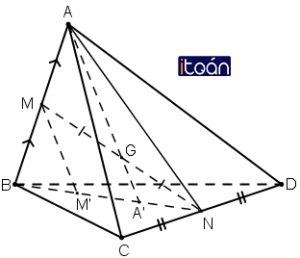
Đề bài cho ta những dữ liệu để giải bài toán như sau : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Lời giải:
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.
Lời kết :
Lượng kiến thức ngày càng lớn yêu cầu các bạn cần nắm bắt tất cả chúng không phải là điều dễ dàng nhưng chỉ cần các bạn quyết tâm và có một lộ trình học tập phù hợp thì hoàn toàn có thể . Bên cạnh học tập trên lớp các bạn nên tìm hiểu thêm nhiều nguồn thông tin học tập mới lạ vừa để rèn luyện và nâng cao kiến thức của bản thân . Itoan sẽ giúp bạn trên chặng đường đi tìm tri thức . Cảm ơn các bạn đã tin tưởng chọn lựa Itoan . Các bạn có thể xem thêm những bài giảng khác tại : https://www.toppy.vn/
Chúc các bạn học tập thật tốt !
Xem thêm :
- Đường thẳng và mặt phẳng – Học tốt toán 11
- Hai đường thẳng song song
- Từ vuông góc đến song song
- Khoảng cách – Hình học 11