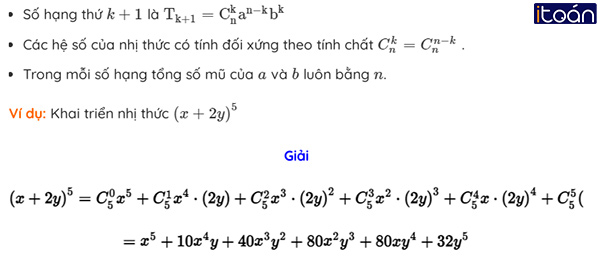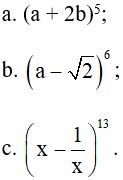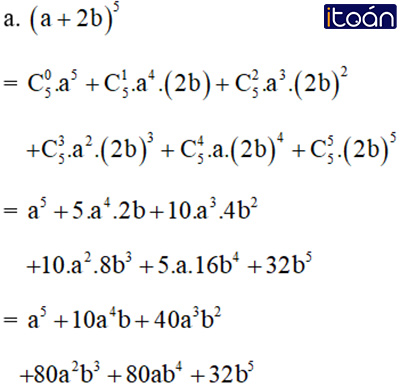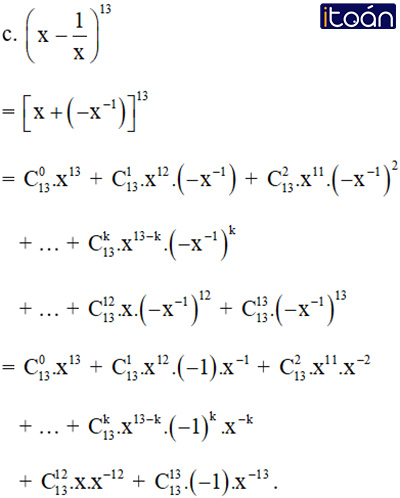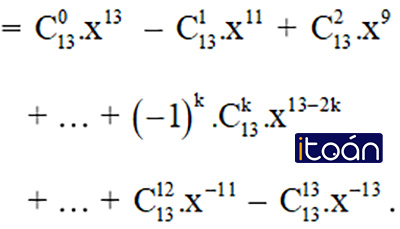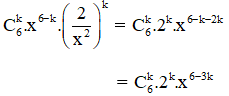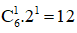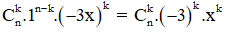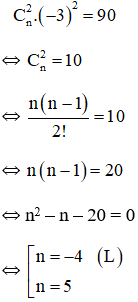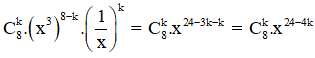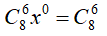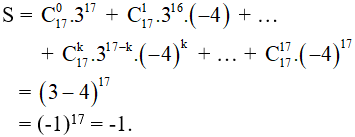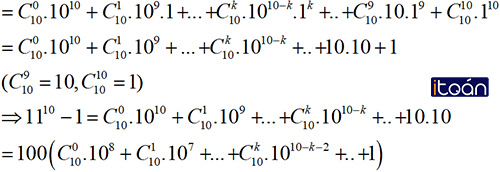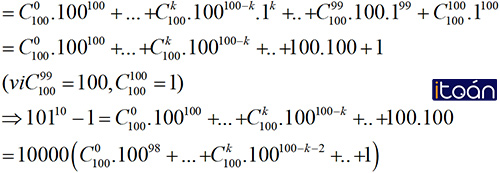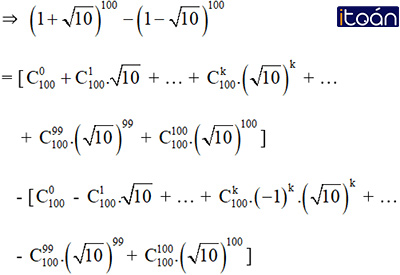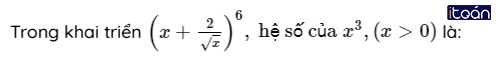Nhị thức Newton – Bài tập & Lời giải Toán lớp 11

Newton là nhà toán học, vật lý học thiên tài. Ông được công nhận là nhà một trong những nhà khoa học vĩ đại, ảnh hưởng nhất mọi thời đại. Trong cuộc đời ông đã tạo ra nhiều giả thuyết, kiến thức có ý nghĩa lớn, một trong số đó là Nhị thức Newton. Bài giảng: Nhị thức Newton được iToan biên soạn với mục đích giúp các em học sinh tổng hợp lại kiến thức lý thuyết và làm tốt các dạng bài tập liên quan. Cùng học với iToan nhé!
Các phần kiến thức trong bài
- Tổng hợp lý thuyết cơ bản cần nắm
- Hướng dẫn giải bài tập SGK
- Bài tập tự luyện giúp em tiến bộ
Tổng hợp lý thuyết về Nhị thức Newton
Công thức nhị thức Newton
c. 💡Chú ý
Trong biểu thức ở vế phải của công thức (1)
- Số các hạng tử là (n+1).
- Các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a0=b0=1
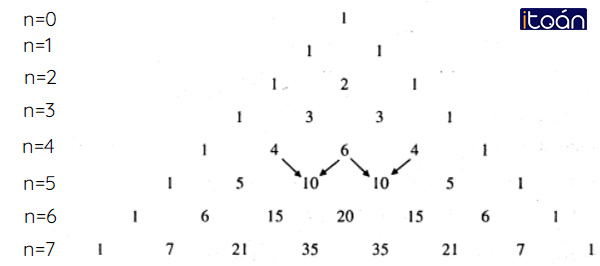
Tam giác Pascan
Trên đây ta thấy muốn khai triển (a+b)^n thành đa thức, ta cần biết n+1 số có mặt trong công thức nhị thức Niu-tơn. Các số này có thể tính được bằng cách sử dụng bảng số sau.
Bảng số này do nhà toán học Pháp Pa-xcan thiết lập vào năm 1653 và được người ta gọi là tam giác Pa-xcan.
Tam giác Pa-xcan được thiết lập theo quy luật sau:
- Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi hai số 1.
- Nếu biết hàng thứ n(n≥1) thì hàng thứ n+1 tiếp theo được thiết lập bằng cách cộng hai số liên tiếp của hàng thứ rồi viết kết quả xuống hàng dưới ở vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.
💡 Chú ý:
 Giải bài tập SGK Toán 11 Nhị thức Newton
Giải bài tập SGK Toán 11 Nhị thức Newton
Bài 1 (trang 57 SGK Đại số 11): Viết khai triển theo công thức nhị thức Niu – tơn:
Lời giải:
Bài 2 (trang 58 SGK Đại số 11): Tìm hệ số của x3 trong khai triển của biểu thức :
Lời giải:
+ Số hạng tổng quát của khai triển 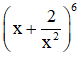
+ x3 ứng với 6 – 3k = 3 ⇔ k = 1.
Vậy hệ số của x3 là:
Bài 3 (trang 58 SGK Đại số 11): Biết hệ số của x2 trong khai triển của (1 – 3x)n là 90. Tìm n.
Lời giải:
+ Số hạng tổng quát của khai triển (1 – 3x)n là:
+ Số hạng chứa x2 ứng với k = 2.
Hệ số của x2 là 90 nên ta có:
Vậy n = 5.
Bài 4 (trang 58 SGK Đại số 11): Tìm số hạng không chứa x trong khai triển của
Lời giải:
+ Số hạng tổng quát trong khai triển 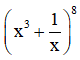
+ Số hạng không chứa x tương ứng với 24 – 4k = 0 ⇔ k = 6.
Vậy số hạng không chứa x trong khai triển đã cho là:
Bài 5 (trang 58 SGK Đại số 11): Tìm khai triển biểu thức (3x – 4)17 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
Lời giải:
Đặt S là tổng các hệ số của đa thức khai triển.
Ta có:
Vậy tổng các hệ số của đa thức khai triển bằng -1.
Bài 6 (trang 58 SGK Đại số 11): Chứng minh rằng:
a) 1110 – 1 chia hết cho 100
b) 101100 – 1 chia hết cho 10.000
c) 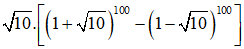
Lời giải:
a) Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )
Do đó, 1110 -1 chia hết cho 100
b) Ta có: 10110 = (100+1)10 ( khai triển nhị thức Niu- tơn )
Do đó, 10110 -1 chia hết cho 10000
Bài tập luyện tập Nhị thức Newton
Các bài tập do iToan biên soạn giúp các em luyện tập tư duy làm bài trắc nghiệm, hiểu và ghi nhớ kiến thức tốt hơn!
Phần câu hỏi
Câu 1: Trong khai triển (2a−b)^5 , hệ số của số hạng thứ 3 bằng:
A. -80
B. 80
C. -10
D. 10
Câu 2:
Câu 3:
A. 60
B. 80
C. 100
D. 160
Câu 4: Trong khai triển (2a−1)^6 , tổng ba số hạng đầu là:
A. 2a^6−6a^5+15a^4 .
B. 2a^6−15a^5+30a^4.
C. 64a^6−192a^5+480a^4
D. 64a^6−192a^5+240a^4.
Phần đáp án
1.B 2.D 3.A 4.D
Lời kết
Nhị thức Newton là phần kiến thức cơ bảng em cần ghi nhớ và thành thạo để có thể học tốt toán Tổ hợp- Xác suất. Để nghe bài giảng chi tiết từ thầy cô và làm thêm các bài tập luyện tập, các em có thể tìm kiếm trên trang web Toppy. Toppy là nền tảng học trực tuyến tốt nhất hiện nay, luôn đem đến cho các em những bài giảng hay, bổ ích, gắn liền với chương trình học trên lớp của các em
Chúc các em học tập tốt!
>> Xem thêm các bài giảng khác tại iToan: