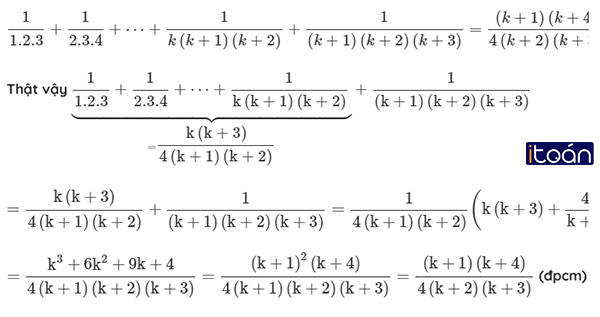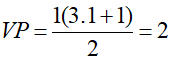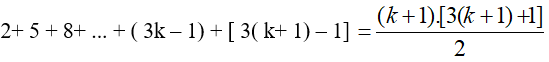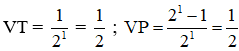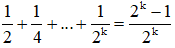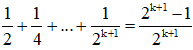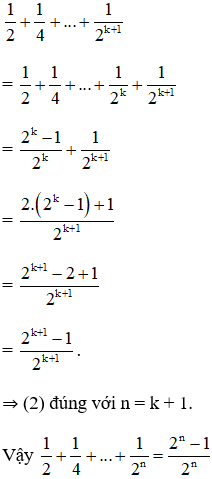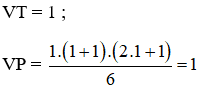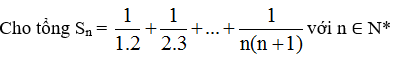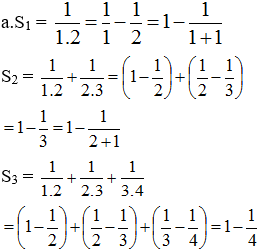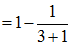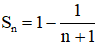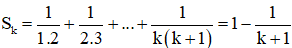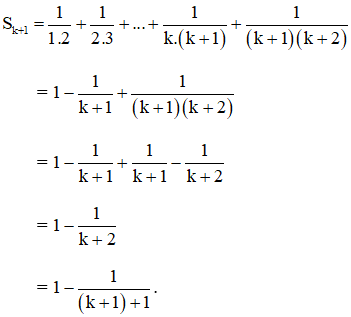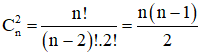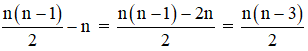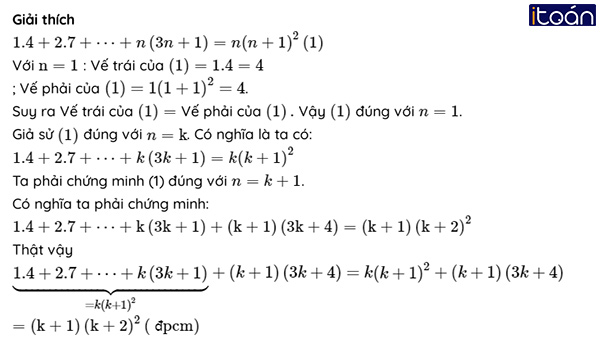Phương pháp quy nạp toán học – Giải bài tập Đại số 11

Trong toán học có vô vàn các phương pháp giải. Để chứng minh một mệnh đề là đúng, không phải lúc nào ta cũng có thể làm theo cách trực tiếp, khi đó, ta có thể dùng phương pháp quy nạp, với những giả sử, giả thuyết. Bài giảng: Phương pháp quy nạp toán học được iToan biên soạn dựa theo chương trình sách giáo khoa Đại số 11, sẽ giúp các em hiểu và nắm bài tốt hơn!
Bài giảng bao gồm 3 phần chính
- Tổng hợp lý thuyết cần nắm và các ví dụ
- Hướng dẫn giải bài tập SGK
- Các bài tập tự luyện
Tổng hợp lý thuyết về Phương pháp quy nạp
Phương pháp quy nạp toán học
Để chứng minh những mệnh đề liên quan đến số tự nhiên n∈N∗ là đúng với mọi n mà không thể thử trực tiếp được thì có thể làm như sau :
Bước 1 : Kiểm tra rằng mệnh đề đúng với n = 1.
Bước 2 : Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k≥1 (gọi là giả thiết quy nạp), chứng minh rằng nó cũng đúng với n = k+1
Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.
🍀 Giả sử P(n) Là một mệnh đề phụ thuộc vào số tự nhiên n. Nếu cả hai điều kiện (i) và (ii) dưới đây được thỏa mãn thì P(n) đúng với mọi n≥m là số tự nhiên cho trước).
(i)P(m) đúng.
(ii) Với mỗi số tự nhiên k≥m, nếu P(k+1) đúng.
🍀Phương pháp chứng minh dựa trên nguyên lý quy nạp toán học gọi là phương pháp quy nạp toán học (hay gọi tắt là phương pháp quy nạp).
CHÚ Ý:
🍀 Để chứng minh một mệnh đề P(n) phụ thuộc vào số tự nhiên n đúng với mọi n≥m là số tự nhiên cho trước), ta thực hiện theo hai bước sau:
Bước 1: Chứng minh rằng P(n) đúng khi n=m .
Bước 2: Với k là một số tự nhiên tùy ý, k≥m . Giả sử P(n) đúng khi n=k, ta sẽ chứng minh P(n) cũng đúng khi n=k+1 . Theo nguyên lý quy nạp toán học, ta kết luận rằng P(n) đúng với mọi số tự nhiên n≥m.
Ví dụ áp dụng
Ví dụ 1: Chứng minh rằng với n∈N∗ thì
a. 1.4+2.7+...+n(3n+1)=n(n+1)2
Giải
a. 1.4+2.7+...+n(3n+1)=n(n+1)2 (1)
Bước 1:
Với n=1: Vế trái của (1) =1.4=4 ; Vế phải của (1) =1(1+1)2=4 . Suy ra Vế trái của (1) = Vế phải của (1). Vậy (1) đúng với n=1.
Bước 2:
Giả sử (1) đúng với n=k . Có nghĩa là ta có: 1.4+2.7+...+k(3k+1)=k(k+1)2 (2)
Ta phải chứng minh (1) đúng với n=k+1 . Có nghĩa ta phải chứng minh:
1.4+2.7+...+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)2
Thật vậy 1.4+2.7+⋯+k(3k+1)=k(k+1)2+(k+1)(3k+4)=k(k+1)2+(k+1)(3k+4)=(k+1)(k+2)2 (đpcm)
Vậy (1) đúng khi n=k+1 . Do đó theo nguyên lí quy nạp, (1) đúng với mọi n∈N∗.
Ta phải chứng minh (2) đúng với n=k+1 . Có nghĩa ta phải chứng minh:
Vậy (2) đúng khi n=k+1 . Do đó theo nguyên lí quy nạp, (2) đúng với mọi n∈N∗.
Ví dụ 2: Chứng minh rằng với n∈N∗ thì 9^n−1 luôn chia hết cho 8.
Giải
Bước 1:
Với n=1: Ta có u1=9^1−1 chia hết cho 8.
Bước 2:
Giả sử với n=k≥1 ta có uk=9^k−1 chia hết cho 8.
Ta cần chứng minh uk+1=9^k+1−1 chia hết cho 8
Thật vậy, ta có uk+1=9^k+1−1=9.9^k−1=9(9^k−1)+8=9uk+8 . Vì 9uk và 8 đều chia hết cho 8, nên uk+1 cũng chia hết cho 8.
Vậy với mọi n∈N∗ thì un chia hết cho 8.
Giải bài tập SGK Đại số 11 Phương pháp quy nạp
Bài 1 (trang 82 SGK Đại số 11):
Chứng minh rằng với n ∈ N*, ta có các đẳng thức:
Lời giải:
a. + Với n = 1, ta có:
VT = 3 – 1 = 2
⇒ VT = VP
⇒ (1) đúng với n = 1
+ Giả sử (1) đúng với n = k ≥ 1 nghĩa là:
2 + 5 + 8 + …+ (3k – 1) = k(3k + 1)/2. (*)
Ta cần chứng minh (1) đúng với n = k + 1, tức là :
Thật vậy :
Ta có :
b) + Với n = 1 :
Vậy (2) đúng với n = 1
+ Giả sử đẳng thức đúng với n = k, tức là:
Cần chứng minh (2) đúng với n = k + 1, tức là:
Thật vậy, ta có :
c. + Với n = 1 :
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
Cần chứng minh (3) đúng khi n = k + 1, tức là:
Thật vậy:
Bài 2 (trang 82 SGK Đại số 11):
Chứng minh rằng với n ∈ N*
a. n3 + 3n2 + 5n chia hết cho 3.
b. 4n + 15n – 1 chia hết cho 9
c. n3 + 11n chia hết cho 6.
Lời giải:
a. Cách 1: Quy nạp
Đặt An = n3 + 3n2 + 5n
+ Ta có: với n = 1
A1 = 1 + 3 + 5 = 9 chia hết 3
+ giả sử với n = k ≥ 1 ta có:
Ak = (k3 + 3k2 + 5k) chia hết 3 (giả thiết quy nạp)
Ta chứng minh Ak + 1 chia hết 3
Thật vậy, ta có:
Ak + 1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3k2 + 6k + 3 + 5k + 5
= (k3 + 3k2 + 5k) + 3k2 + 9k + 9
Theo giả thiết quy nạp: k3 + 3k2 + 5k ⋮ 3
Mà 3k2 + 9k + 9 = 3.(k2 + 3k + 3) ⋮ 3
⇒ Ak + 1 ⋮ 3.
Cách 2: Chứng minh trực tiếp.
Có: n3 + 3n2 + 5n
= n.(n2 + 3n + 5)
= n.(n2 + 3n + 2 + 3)
= n.(n2 + 3n + 2) + 3n
= n.(n + 1)(n + 2) + 3n.
Mà: n(n + 1)(n + 2) ⋮ 3 (tích của ba số tự nhiên liên tiếp)
3n ⋮ 3
⇒ n3 + 3n2 + 5n = n(n + 1)(n + 2) + 3n ⋮ 3.
Vậy n3 + 3n2 + 5n chia hết cho 3 với mọi ∀n ∈ N*
>> Xem thêm các bài giảng khác tại: Toppy.
b. 4n + 15n – 1 chia hết cho 9
Đặt An = 4n + 15n – 1
với n = 1 ⇒ A1 = 4 + 15 – 1 = 18 chia hết 9
+ giả sử đúng với n = k ≥ 1 nghĩa là:
Ak = (4k + 15k – 1) chia hết 9 (giả thiết quy nạp)
Ta cần chứng minh: Ak + 1 chia hết 9
Thật vậy, ta có:
Ak + 1 = 4k+1 + 15(k + 1) – 1
= 4.4k + 15k + 15 – 1
= 4.(4k + 15k – 1) – 45k+ 4+ 15 – 1
= 4.(4k +15k- 1) – 45k + 18
= 4. Ak + (- 45k + 18)
Ta có: Ak⋮ 9 và ( – 45k+ 18) = 9(- 5k + 2)⋮ 9
Nên Ak + 1 ⋮ 9
Vậy 4n + 15n – 1 chia hết cho 9 ∀n ∈ N*
c. Đặt Un = n3 + 11n
+ Với n = 1 ⇒ U1 = 12 chia hết 6
+ giả sử đúng với n = k ≥ 1 ta có:
Uk = (k3 + 11k) chia hết 6 (giả thiết quy nạp)
Ta cần chứng minh: Uk + 1 = (k + 1)3 + 11(k + 1) chia hết 6
Thật vậy ta có:
Uk+1 = (k + 1)3 + 11(k +1)
= k3 + 3k2 + 3k + 1 + 11k + 11
= (k3 + 11k) + 3k2 + 3k + 12
= Uk + 3(k2 + k + 4)
Mà: Uk ⋮ 6 (giả thiết quy nạp)
3.(k2 + k + 4) ⋮ 6. (Vì k2 + k + 4 = k(k + 1) + 4 ⋮2)
⇒ Uk + 1 ⋮ 6.
Vậy n3 + 11n chia hết cho 6 ∀n ∈ N*.
Bài 3 (trang 82 SGK Đại số 11):
Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:
a.3n > 3n + 1
b.2n+1 > 2n + 3
Lời giải:
a. Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.
b. 2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.
Bài 4 (trang 83 SGK Đại số 11):
a.Tính S1, S2, S3
b.Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
Lời giải:
b. Dự đoán:
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
Khi đó:
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
Bài 5 (trang 83 SGK Đại số 11):
Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là n(n-3)/2
Lời giải:
Đa giác lồi n cạnh có n đỉnh.
Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.
⇒Tổng số cạnh và đường chéo của đa giác bằng:
⇒ số đường chéo của đa giác lồi có n cạnh là:
Bài tập tự luyện Phương pháp quy nạp
Làm thành thạo các bài tập tự luyện sẽ giúp các em hiểu và nhớ kiến thức lâu hơn!
Phần câu hỏi
Câu 1: Chứng minh rằng với moi số nguyên n, ta có:
1.4+2.7+⋯+n(3n+1)=n(n+1)^2
Câu 2: Chứng minh rằng với moi số nguyên n, ta có:
Lời giải:
Lời kết
Bài giảng: Phương pháp quy nạp toán học kết thúc tại đây. Hy vọng sau bài này, các em sẽ có một cách tư duy mới mẻ hơn khi giải các bài toán khó, bởi toán học không chỉ là những công thức, mà là tư duy sáng tạo, logic. Cùng học tốt với Toppy nhé!
>> Xem thêm các bài giảng khác tại: Toppy.
>> Xem thêm:
- Nguyên hàm
- Phương trình lượng giác cơ bản cần nhớ
- Tích phân- Đại số 12
- Tứ giác nội tiếp đường tròn
- Tính chất chia hết của một tổng