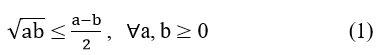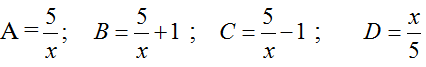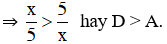Bất đẳng thức – Tổng hợp lý thuyết và luyện tập đại số lớp 10
Bất đẳng thức là một chuyên đề các em đã được làm quen trước đây. Tuy nhiên, với đại số lớp 10, một lần nữa các em sẽ được gặp lại khái niệm này. Với lượng kiến thức lớn và chuyên sâu hơn. Đồng thời, các dạng bài tập cũng được mở rộng và nâng lên ở mức khó. Vì thế, hãy cùng Itoan tập trung học và cùng nhau luyện tập thêm về chuyên đề này nhé!
Bất đẳng thức – Tổng hợp những lý thuyết quan trọng
Khái niệm bất đẳng thức
Bất đẳng thức có thể được hiểu là các mệnh đề dạng A > B hoặc A < B.
Nếu ta có C > D là hệ quả có thể suy ra từ A > B. Ta nói C > D là bất đẳng thức hệ quả của A>B. Có thể viết A > B => C > D
Nếu ta có C > D là hệ quả có thể suy ra từ A > B và ngược lại, từ C > D ta cũng có thể suy ra A > B. Ta gọi chúng là những bất đẳng thức tương đương nhau. Có thể viết A > B <=> C > D
Tính chất
Ta có các tính chất của chúng như sau:
- Cộng hai vế của một BĐT với một số
- Nhân hai vế của một BĐT với một số
- Cộng hai BĐT cùng chiều
- Nhân hai BĐT cùng chiều
- Nâng hai vế của BĐT lên một lũy thừa
- Khai căn hai vế của một BĐT
Cụ thể về các tính chất trên, mời các bạn xem tại bảng sau:
Chú ý: Đối với dạng bất đẳng thức a ≤ b hoặc a ≥ b, ta cũng có thể sử dụng các tính chất trên. Và thực hiện tính toán như đối với các bất đẳng thức thông thường.
Bất đẳng thức Cosi
Định lí
Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng
Đẳng thức 
xảy ra khi và chỉ khi a = b.
Các hệ quả
Hệ quả 1
Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
a +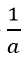 
≥ 2, ∀a > 0.
Hệ quả 2
Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x = y.
Hệ quả 3
Nếu x, y cùng dương và có tích không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y.
BĐT chứa dấu giá trị tuyệt đối
Các dạng bài tập luyện tập cần lưu ý
Bài 1 (trang 79 SGK Đại Số 10):
Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?
a) 8x > 4x ; b) 4x > 8x
c) 8x2 > 4x2 ; d) 8 + x > 4 + x
Lời giải
a) Ta có: 8 > 4 nên để 8x > 4x thì x > 0
Do đó, chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a sai)
b) Ta có: 4 < 8 nên để 4x > 8x thì x < 0 .
Do đó, khẳng định chỉ đúng khi x < 0
c) chỉ đúng khi x ≠ 0
d) Ta có: 8 > 4 nên với mọi x thì 8+ x > 4+ x ( tính chất cộng hai vế của BĐT với 1 số)
Do đó, khẳng định đúng với mọi x.
Vậy khẳng định d là đúng với mọi giá trị của x.
Bài 2 (trang 79 SGK Đại Số 10):
Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?
Lời giải
Với mọi x ≠ 0 ta luôn có: – 1 < 0 < 1. Do đó,
hay C < A < B.
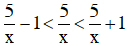
Lại có x > 5 ⇒ x2 > 52 (Bình phương hai vế)
⇒ 
(Nhân cả hai vế của bất đẳng thức với 
)
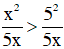
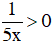
Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.
Bài 3 (trang 79 SGK Đại Số 10):
Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b – c)2 < a2
b) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
Lời giải
a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
Lời kết
Trên đây là bài viết nội dung về chủ đề Bất đẳng thức. Hy vọng đây sẽ là những kiến thức bổ ích dành cho các bạn học sinh. Đặc biệt là quý phụ huynh có nhu cầu ôn tập và giảng dạy cho các em. Trong quá trình học tập và ôn luyện, nếu có nhu cầu tìm kiếm đơn vị học tập uy tín, chất lượng. Hoặc muốn được giải đáp về những kiến thức liên quan đến môn học, hãy liên hệ với Itoan để được giải đáp nhanh nhất có thể
