Các kiến thức cần nhớ về hàm số bậc hai – Toán 10 Đại số

• Hàm số bậc hai được cho bởi công thức: y=ax2+bx+c(a≠0).
• Tập xác định: D=R.
• Hàm số y=ax2(a≠0) đã học ở lớp 9 là một trường hợp riêng của hàm số này.

Đồ thị của hàm số bậc 2

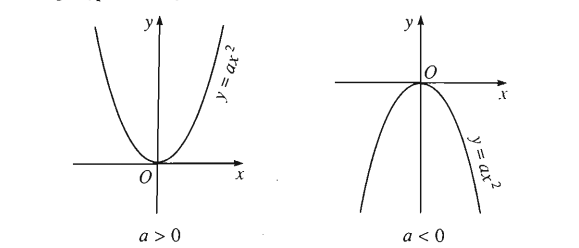
1. Nhắc lại về đồ thị hàm số y=ax2(a≠0)

Đồ thị hàm số y=ax2(a≠0) là một parabol nhận trục Oy là trục đối xứng, có đỉnh là điểm O(0;0)  . Đây là điểm thấp nhất của đồ thị trong trường hợp a>0 (y≥0 với mọi  x), và là điểm cao nhất của đồ thị trong trường hợp a<0 (y≥0 với mọi x ).

2. Đồ thị hàm số y=ax2+bx+c(a≠0)

a. Nhận xét

y=ax2+bx+c=a(x+b2a)2+−Δ4a với Δ=b2−4ac.

• Nếu x=−b2a thì y=−Δ4a. Vậy điểm I(−b2a;−Δ4a) thuộc đồ thị hàm số y=ax2+bx+c(a≠0).
• Nếu a>0 thì y≥−Δ4a với mọi x , do đó I là điểm thấp nhất của đồ thị.
• Nếu a<0 thì y≤−Δ4a với mọi x, do đó I là điểm cao nhất của đồ thị.
• Như vậy, điểm I(−b2a;−Δ4a) đối với đồ thị hàm số y=ax2+bx+c(a≠0) đóng vai trò như đỉnh O(0;0) của parabol y=ax2(a≠0) .

b. Đồ thị

Đồ thị của hàm số y=ax2+bx+c(a≠0) là một đường parabol có đỉnh là điểm I(−b2a;−Δ4a) , có trục đối xứng là đường thẳng x=−b2a  . Parabol này quay bề lõm lên trên nếu a>0 , xuống dưới nếu a<0 .

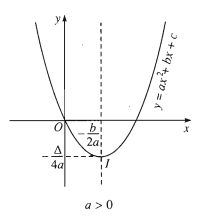
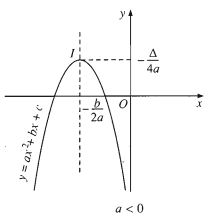
c. Cách vẽ 

Để vẽ đồ thị hàm số y=ax2+bx+c(a≠0), ta thực hiện các bước sau:

Bước 1: Xác định tọa độ đỉnh I(−b2a;−Δ4a).

Bước 2: Vẽ trục đối xứng x=−b2a.

Bước 3: Xác định tọa độ các giao điểm của Parabol với trục tung và trục hoành (nếu có)

Xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm (0;c) qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn.

Bước 4: Vẽ parabol

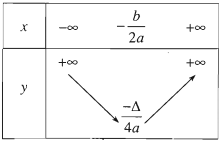
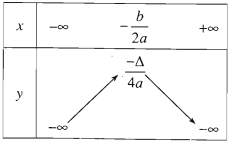
3. Chiều biến thiên của hàm số bậc hai 

Nếu a>0 thì hàm số y=ax2+bx+c

• Nghịch biến trên khoảng (−∞;−b2a).
• Đồng biến trên khoảng (−b2a;+∞).

Nếu a<0 thì hàm số y=ax2+bx+c

• Đồng biến trên khoảng (−∞;−b2a).
• Nghịch biến trên khoảng (−b2a;+∞).

Trên là tổng hợp kiến thức về hàm số bậc 2 mà các bạn học sinh cần nắm vững. Itoan hy vọng phần tổng hợp này giúp các bạn học sinh học và luyện tập hiệu quả.

Xem thêm:

Tổng hợp lý thuyết về hàm số – Đại số Toán 10

Hàm số y = ax + b – Tổng hợp lý thuyết và các dạng bài liên quan