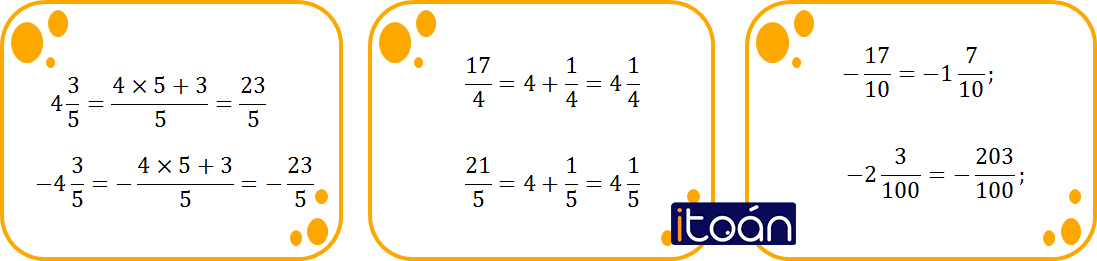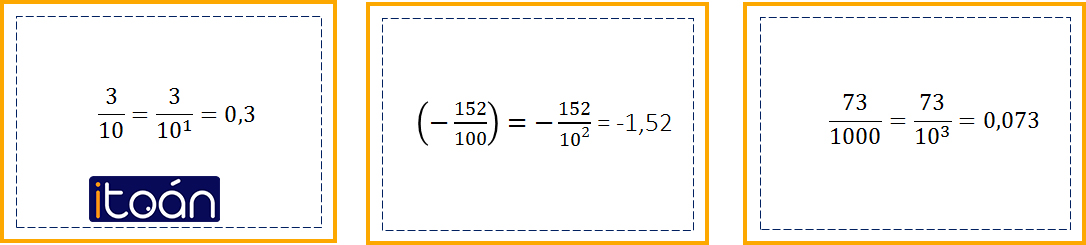Hỗn số- Học tốt toán lớp 6

5/5 - (5 bình chọn)

Bài học hôm nay , chúng ta sẽ cùng nhau đi tìm hiểu về “ Hỗn số ” . Như các em đã biết thì chúng ta cùng đã được tiệp cận với các bài tập liên quan đến hỗn số ở cấp học trước nhưng trong bài hôm nay , chúng ta sẽ được nâng cao các lý thuyết cũng như bài tập liên quan .Vì vậy , các bạn hãy thật tập trung và hiểu bài để có thể hoàn thiện được các bài tập được giao nhé . Kính mời các bậc phụ huynh và quý thầy cô tham khảo bài giảng sau đây.

Vào học ngay cùng Itoan nào các bạn nhỏ ơi !

Mục tiêu bài học : Hỗn số

Nhắc lại một số kiến thức cơ bản đã được học ở cấp trước
Trình bày thêm những lý thuyết , các dạng bài tập của bài hỗn số , số thập phân , phần trăm
Hoàn thiện các bài tập từ cơ bản đến nâng cao , nắm bắt được các phương pháp làm bài

Kiến thức cơ bản của bài học : Hỗn số

Dưới đây là phần lý thuyết của bài học , mong các bạn tập trung ghi chép lại các ý chính để việc học tập thêm hiệu quả

I. Hỗn số

Nếu phân số dương lớn hơn 1, ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu, thương tìm được là phần nguyên của hỗn số, số dư là tử của phân số kèm theo, còn mẫu vẫn là mẫu đã cho.

Muốn viết một hỗn số dưới dạng một phân số, ta nhân phần nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử số của phân số, còn mẫu vẫn là mẫu đã cho.

Chú ý:

- - - Đối với các hỗn số có dấu “−” đằng trước thì khi đổi sang phân số ta đổi số đối của nó theo quy tắc thông thường rồi viết thêm dấu “−” đằng trước phân số tìm được, tuyệt đối không lấy phần số nguyên âm nhân với mẫu rồi cộng tử số.
    - Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu “−” trước kết quả nhận được.

Ví dụ:

hon-so

II. Số thập phân

Định nghĩa về số thập phân :Phân số thập phân là phân số mà mẫu là lũy thừa của 10.

Số thập phân gồm hai phần được phân chia như sau :

- - - Phần số nguyên viết bên trái dấu phẩy
    - Phần thập phân viết bên phải dấu phẩy

Ví dụ:

hon-so

III. Phần trăm

Những phân số có mẫu là 100 còn được viết dưới dạng phần trăm với kí hiệu %.

Ví dụ:

hon-so

Hướng dẫn giải bài tập toán SKG Toán 6 bài : Hỗn số

Sau đây để kiểm tra cũng như nhắc lại những kiến thức đã học , chúng ta cùng làm một số bài tập SGK Toán 6 sau đây :

Bài 1 :

Viết các phân số sau dưới dạng hỗn số:

$\frac{6}{5};\,\,\,\,\frac{7}{3};\,\,\, - \frac{{16}}{{11}}$

Hướng dẫn:

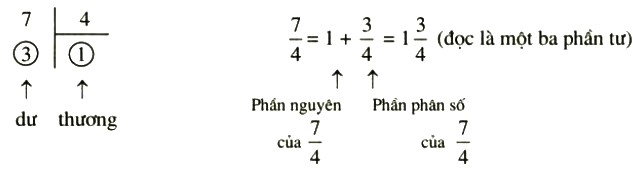
Giải Toán lớp 6 bài 13: Phép chia phân số: Hỗn số - Số thập phân - Phần trăm

Lời giải:

$\frac{6}{5} = \frac{5}{5} + \frac{1}{5} = 1 + \frac{1}{5} = 1\frac{1}{5}$

$\frac{7}{3} = \frac{6}{3} + \frac{1}{3} = 2 + \frac{1}{3} = 2\frac{1}{3}$

$- \frac{{16}}{{11}} = - \frac{{11}}{{11}} - \frac{5}{{11}} = - \left( {1 + \frac{5}{{11}}} \right) = - 1\frac{5}{{11}}$

Bài 2 :

Viết các hỗn số sau dưới dạng phân số:

$5\frac{1}{7};\,\,\,\,6\frac{3}{4};\,\,\, - 1\frac{{12}}{{13}}$

Lời giải:

$5\frac{1}{7} = \frac{{5.7 + 1}}{7} = \frac{{36}}{7};\,\,6\frac{3}{4} = \frac{{6.4 + 3}}{4} = \frac{{27}}{4};\,\,\, - 1\frac{{12}}{{13}} = - \frac{{13.1 + 12}}{{13}} = \frac{{25}}{{13}}$

Bài 3 :

So sánh những phân số sau đây :

$\frac{22}{7}$ và $\frac{34}{11}$

Lời giải:

Có $\frac{{22}}{7} = \frac{{21}}{7} + \frac{1}{7} = 3 + \frac{1}{7} = 3\frac{1}{7};\,\,\,\frac{{34}}{{11}} = \frac{{33}}{{11}} + \frac{4}{{11}} = 3 + \frac{4}{{11}} = 3\frac{4}{{11}}$

Vì $\frac{1}{7} < \frac{4}{{11}}$ nên $3\frac{1}{7} < 3\frac{4}{{11}}$ hay $\frac{{22}}{7} < \frac{{34}}{{11}}$

Bài 4 :

Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân).

3dm, 85cm, 52mm.

Hướng dẫn: Dựa vào những kiến thức đã học , chúng ta sẽ có những kiến thức cơ bản sau :

1dm = $\frac{1}{{10}}$ m; 1cm = $\frac{1}{{100}}$ m và 1mm = $\frac{1}{{1000}}$ m

Lời giải:

3dm = $\frac{3}{{10}}$ m = 0,3m; 85cm = $\frac{{85}}{{100}}$ m = 0,85m; 52mm = $\frac{{52}}{{1000}}$ m = 0,052m

Bài 5 :

Dùng phần trăm với kí hiệu % để viết các số phần trăm trong các câu sau đây :

Để đạt tiêu chuẩn công nhận phổ cập giáo dục THCS, xã Bình Minh đã đề ra chỉ tiêu phấn đấu:

– Huy động số trẻ 6 tuổi đi học lớp 1 đạt chín mươi mốt phần trăm. Có ít nhất tám mươi hai phần trăm số trẻ ở độ tuổi 11 – 14 tốt nghiệp Tiểu học;

– Huy động chín mươi sáu phần trăm học sinh tốt nghiệp Tiểu học hàng năm vào lớp 6 THCS phổ thông và THCS bổ túc;

– Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ chín mươi tư phần trăm trở lên.

Lời giải:

– Theo như đề bài đã cho ta nhận thấy , Huy động số trẻ 6 tuổi đi học lớp 1 đạt 91%. Có ít nhất 82% số trẻ ở độ tuổi 11 – 14 tốt nghiệp Tiểu học;

– Sử dụng kiến thức vừa học về cách viết , ta có thể viết thành :Huy động 96% học sinh tốt nghiệp Tiểu học hàng năm vào lớp 6 THCS phổ thông và THCS bổ túc;

– Thông qua những kiến thức đã học , chúng ta có thể chuyển đổi thành câu sau :Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ 94% trở lên.

Bài 6 :

Khi cộng hai hỗn số $3\frac{1}{5}$ và $2\frac{2}{3}$ bạn Cường làm như sau:

$3\frac{1}{5} + 2\frac{2}{3} = \frac{{16}}{5} + \frac{8}{3} = \frac{{48}}{{15}} + \frac{{40}}{{15}} = \frac{{88}}{{15}} = 5\frac{{13}}{{15}}$

a) Bạn Cường đã tiến hành cộng hai hỗn số như thế nào?

b) Có cách nào tính nhanh hơn không?

Lời giải:

a) Bạn Cường đã tiến hành cộng hai hỗn số bằng cách đổi các hỗn số về dạng phân số và thực hiện phép cộng phân số.

b) Cách nhanh hơn: cộng hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.

Bài 7 :

Tính giá trị của các biểu thức:

Lời giải:

$A = 8\frac{2}{7} - \left( {3\frac{4}{9} + 4\frac{2}{7}} \right) = \frac{{58}}{7} - \left( {\frac{{31}}{9} + \frac{{30}}{7}} \right)$

$= \frac{{58}}{7} - \frac{{31}}{9} - \frac{{30}}{7} = \frac{{28}}{7} - \frac{{31}}{9} = 4 - \frac{{31}}{9} = \frac{5}{9}$

$B = \left( {10\frac{2}{9} + 2\frac{3}{5}} \right) - 6\frac{2}{9} = 10\frac{2}{9} + 2\frac{3}{5} - 6\frac{2}{9}$

$= \left( {10\frac{2}{9} - 6\frac{2}{9}} \right) + 2\frac{3}{5} = 4 + 2\frac{3}{5} = 6\frac{3}{5}$

Bài 8 :

Thực hiện phép nhân hoặc chia hai hỗn số bằng cách viết hỗn số dưới dạng phân số:

Hướng dẫn:

Để thực hiện được phép toán , các bạn cần đổi các hỗn số về dạng phân số và thực hiện phép nhân và chia phân số.

Lời giải:

$5\frac{1}{2}.3\frac{3}{4} = \frac{{11}}{2}.\frac{{15}}{4} = \frac{{165}}{8} = 20\frac{5}{8}$

$6\frac{1}{3}:4\frac{2}{9} = \frac{{19}}{3}:\frac{{38}}{9} = \frac{{19}}{3}.\frac{9}{{38}} = \frac{3}{2} = 1\frac{1}{2}$

Bài 10 :

Bạn Hoàng làm phép nhân $4\frac{3}{7}.2$ như sau:

$4\frac{3}{7}.2 = \frac{{31}}{7}.2 = \frac{{31}}{7}.\frac{2}{1} = \frac{{62}}{7} = 8\frac{6}{7}$

Có cách nào tính nhanh hơn không? Nếu có, hãy giải thích cách làm đó.

Lời giải:

$4\frac{3}{7}.2 = \left( {4.2} \right) + \left( {\frac{3}{7}.2} \right) = 8 + \frac{6}{7} = 8\frac{6}{7}$

Bài 11 :

a) Khi chia một số cho 0,5 ta chỉ việc nhân số đó với 2.

Ví dụ: 37 : 0,5 = 37.2 = 74

102 : 0,5 = 102.2 = 204

Hãy giải thích tại sao lại làm như vậy?

b) Hãy tìm hiểu các làm tương tự khi chia một số cho 0,25; cho 0,125.

Cho các ví dụ minh họa.

Lời giải:

a) Vì $0,5 = \frac{5}{{10}} = \frac{1}{2}$ nên khi chia cho 0,5 ta nhân số đó với nghịch đảo của phân số $\frac{1}{2}$ tức là nhân với 2.

b) Vì $0,25 = \frac{1}{4}$ nên khi chia một số cho 0,25 ta chỉ việc nhân số đó với 4.

Ví dụ: 15 : 0,25 = 15.4 = 60

Vì $0,125 = \frac{1}{8}$ nên khi chia một số cho 0,125 ta chỉ việc nhân số đó với 8.

ví dụ: 25 : 0,125 = 25.8 = 200

Bài 12 :

Viết các phân số sau dưới dạng số thập phân và dùng kí hiệu %:

$\frac{7}{{25}};\,\,\,\frac{{19}}{4};\,\,\,\frac{{26}}{{65}}$

Lời giải:

$\frac{7}{{25}} = \frac{{28}}{{100}} = 28\% ;\,\,\,\frac{{19}}{4} = \frac{{475}}{{100}} = 475\% ;\,\,\,\frac{{26}}{{65}} = \frac{2}{5} = \frac{{40}}{{100}} = 40\%$

Bài 13:

Viết các phần trăm sau dưới dạng số thập phân:

7%; 45%; 216%

Lời giải:

$7\% = \frac{7}{{100}} = 0,07;\,\,\,\,45\% = \frac{{45}}{{100}} = 0,45;\,\,\,216\% = \frac{{216}}{{100}} = 2,16$

Bài 14 :

Hoàn thành các phép tính sau:

$\begin{gathered} \frac{7}{9} + \frac{5}{{12}} - \frac{3}{4} = \frac{{7.4}}{{36}} + \frac{{5. \ldots }}{{36}} - \frac{{3. \ldots }}{{36}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ = \frac{{28 + \ldots - \ldots }}{{36}} \hfill \\ \,\,\,\,\, = \frac{{16}}{{36}} = \frac{ \ldots }{ \ldots } \hfill \\ \end{gathered}$

Lời giải:

$\begin{gathered} \frac{7}{9} + \frac{5}{{12}} - \frac{3}{4} = \frac{{7.4}}{{36}} + \frac{{5. 3 }}{{36}} - \frac{{3. 9 }}{{36}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{28 + 15 - 27 }}{{36}} \hfill \\ \,\,\,\,\,\,\,\,\,\ = \frac{{16}}{{36}} = \frac{ 4 }{ 9 } \hfill \\ \end{gathered}$

Bài 15 :

Tính:

a) $\frac{1}{3} + \frac{3}{8} - \frac{7}{{12}}$	b) $\frac{{ - 3}}{{14}} + \frac{5}{8} - \frac{1}{2}$
c) $\frac{1}{4} - \frac{2}{3} - \frac{{11}}{{18}}$	d) $\frac{1}{4} + \frac{5}{{12}} - \frac{1}{{13}} - \frac{7}{8}$

Lời giải:

$\frac{1}{3} + \frac{3}{8} - \frac{7}{{12}} = \frac{{24}}{{72}} + \frac{{27}}{{72}} - \frac{{42}}{{72}} = \frac{9}{{72}} = \frac{1}{8}$

$\frac{{ - 3}}{{14}} + \frac{5}{8} - \frac{1}{2} = \frac{{ - 12}}{{56}} + \frac{{35}}{{56}} - \frac{{28}}{{56}} = \frac{{ - 5}}{{56}}$

$\frac{1}{4} - \frac{2}{3} - \frac{{11}}{{18}} = \frac{9}{{36}} - \frac{{24}}{{36}} - \frac{{22}}{{36}} = \frac{{ - 37}}{{36}}$

$\frac{1}{4} + \frac{5}{{12}} - \frac{1}{{13}} - \frac{7}{8} = \frac{{78}}{{312}} + \frac{{780}}{{312}} - \frac{{24}}{{312}} - \frac{{273}}{{312}} = \frac{{561}}{{312}}$

Bài 16 :

Hoàn thành các phép tính sau:

a) Tính tổng: $1\frac{3}{4} + 3\frac{5}{9}$

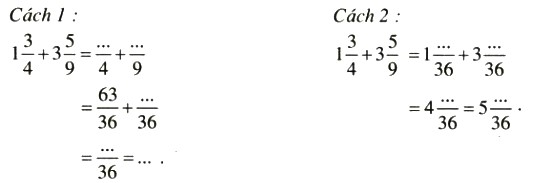
Giải Toán lớp 6 bài 13: Hỗn số - Số thập phân - Phần trăm

b) Tính hiệu: $3\frac{5}{6} - 1\frac{9}{{10}}$

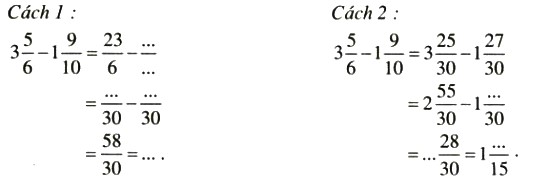
Giải Toán lớp 6 bài 13: Hỗn số - Số thập phân - Phần trăm

Lời giải:

a) $1\frac{3}{4} + 3\frac{5}{9}$

$1\frac{3}{4} + 3\frac{5}{9} = 1\frac{{27}}{{36}} + 3\frac{{20}}{{36}} = 4\frac{{47}}{{36}} = 5\frac{{11}}{{36}}$

b) $3\frac{5}{6} - 1\frac{9}{{10}}$

$3\frac{5}{6} - 1\frac{9}{{10}} = 3\frac{{25}}{{30}} - 1\frac{{27}}{{30}} = 2\frac{{55}}{{30}} - 1\frac{{27}}{{30}} = 1\frac{{28}}{{30}} = 1\frac{{14}}{{15}}$

Bài 17 :

Tính bằng hai cách:

Lời giải:

Để giải cho các phép tính dưới đây , các bạn có thể thực hiện theo 2 cách dưới đây :

a) $2\frac{4}{9} + 1\frac{1}{6}$

Cách 1: $2\frac{4}{9} + 1\frac{1}{6} = \frac{{22}}{9} + \frac{7}{6} = \frac{{132}}{{54}} + \frac{{63}}{{54}} = \frac{{195}}{{54}} = 3\frac{{33}}{{54}}$

Cách 2: $2\frac{4}{9} + 1\frac{1}{6} = 2\frac{{24}}{{54}} + 1\frac{9}{{54}} = 3\frac{{33}}{{54}}$

b) $7\frac{1}{8} - 5\frac{3}{4}$

Cách 1: $7\frac{1}{8} - 5\frac{3}{4} = \frac{{57}}{8} - \frac{{23}}{4} = \frac{{57}}{8} - \frac{{46}}{8} = \frac{{11}}{8} = 1\frac{3}{8}$

Cách 2: $7\frac{1}{8} - 5\frac{3}{4} = 7\frac{1}{8} - 5\frac{6}{8} = 6\frac{9}{8} - 5\frac{6}{8} = 1\frac{3}{8}$

c) $4 - 2\frac{6}{7}$

Cách 1: $4 - 2\frac{6}{7} = \frac{{28}}{7} - \frac{{20}}{7} = \frac{8}{7} = 1\frac{1}{7}$

Cách 2: $4 - 2\frac{6}{7} = 3\frac{7}{7} - 2\frac{6}{7} = 1\frac{1}{7}$

Lời kết :

Bài học của chúng ta đã kết thúc . Cô mong các bạn đều nắm bắt được bài tập thật tốt và áp dụng vào giải các loại bài tập liên quan đến kiến thức bài học từ cơ bản đến nâng cao . Bài học rất dài và đây có thể là kiến thức mới mẻ với nhiều bạn học sinh .Chính vì vậy , các bạn cần chăm chỉ ghi chép bài cũng như hoàn thành các bài tập . Các bạn có thể tham khảo thêm tại địa chỉ : https://www.toppy.vn/ để học được nhiều mẹo hay về học tập .

Chúc các bạn học tốt !

Xem thêm :

Hỗn số- Học tốt toán lớp 6

Mục tiêu bài học : Hỗn số

Kiến thức cơ bản của bài học : Hỗn số

I. Hỗn số

II. Số thập phân

III. Phần trăm

Hướng dẫn giải bài tập toán SKG Toán 6 bài : Hỗn số

Bài 5 :

Bài 7 :

Bài 10 :

Bài 11 :

Bài 15 :

Bài 16 :

Bài 17 :

Lời kết :

Quỳnh Nguyễn

Trả lời Hủy

Mục tiêu bài học : Hỗn số

Kiến thức cơ bản của bài học : Hỗn số

I. Hỗn số

II. Số thập phân

III. Phần trăm

Hướng dẫn giải bài tập toán SKG Toán 6 bài : Hỗn số

Bài 5 :

Bài 7 :

Bài 10 :

Bài 11 :

Bài 15 :

Bài 16 :

Bài 17 :

Lời kết :

Quỳnh Nguyễn

Tỉ lệ thức - Bài tập & Lời giải SGK Toán lớp 7

Biểu đồ phần trăm - Học tốt toán lớp 6

Trả lời Hủy