Khái niệm hai tam giác đồng dạng – Hình học Toán 8

Hai tam giác đồng dạng là kiến thức rất quan trọng mà học sinh cần phải nắm rõ trong chương trình Toán 8. Để tìm hiểu rõ hơn về khái niệm hai tam giác đồng dạng và ba trường hợp đồng dạng. Hãy tham khảo ngay bài viết sau đây của Itoan các bạn nhé.
Khái niệm hai tam giác đồng dạng
Khi cho 2 tam giác ABC và tam giác A’B’C’. Ta xét các cặp góc và tính tỷ số 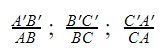
2 tam giác ABC và A’B’C’ sẽ được xem là đồng dạng <=> góc A = góc A’, góc B = góc B’, góc C = góc C’ và 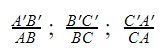 .
.
Như vậy, 2 tam giác sẽ được xem là đồng dạng với nhau <=> 2 tam giác đó có các góc tương ứng bằng nhau và các cạnh có tỷ lệ tương ứng với nhau.
Ký hiệu của 2 tam giác đồng dạng
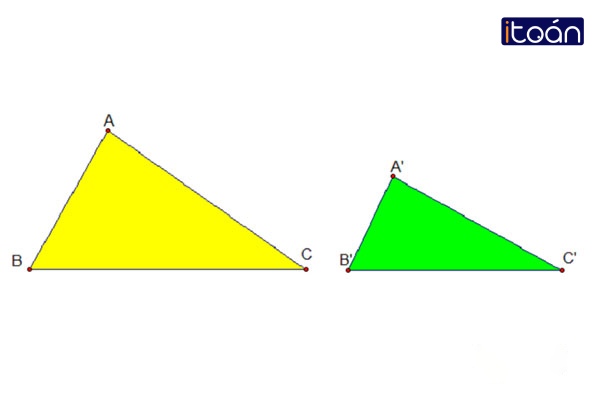
Cho 2 tam giác ABC và A’B’C’, 2 tam giác đồng dạng với nhau sẽ có ký hiệu là:
△ABC ∼ △A’B’C’
Khi các cạnh có tỷ số tương ứng là k = 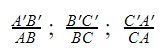 thì k sẽ được gọi là tỷ số đồng dạng.
thì k sẽ được gọi là tỷ số đồng dạng.
Tính chất của 2 tam giác đồng dạng
Theo như khái niệm hai tam giác đồng dạng, chúng ta có thể suy ra được 3 tính chất cơ bản sau đây:
- Mỗi tam giác đồng dạng với chính bản thân nó.
- Nếu △ABC ∼ △A’B’C’ thì △A’B’C’ ∼ △ABC.
- Nếu 2 tam giác đều cùng đồng dạng với một tam giác khác thì 2 tam giác đó sẽ đồng dạng với nhau. Ký hiệu: Nếu △A’B’C’ ∼ △A”B”C” và △A”B”C” ∼ △ABC thì △ABC ∼ △A’B’C’.
Lưu ý: hai tam giác bằng nhau thì đồng dạng nhưng hai tam giác đồng dạng không có nghĩa là bằng nhau.
Định lý liên quan đến hai tam giác đồng dạng
Định lý: Nếu có 1 đường thẳng song song với 2 cạnh của một tam giác và đồng thời cắt cạnh còn lại của tam giác đó. => Sẽ tạo thành một tam giác mới, tam giác đó sẽ đồng dạng với tam giác đã được cho trước.
Nói cách khác, với △ABC đã cho trước:
- Điểm D ∈ AB
- Điểm E ∈ AC
=> Ta sẽ có △ABC ∼ △ADE. Đặc biệt, định lý này cũng có thể áp dụng với trường hợp có một đường thẳng d cắt đoạn kéo dài của 2 đoạn thẳng trong tam giác và đồng thời song song với đoạn còn lại.
Những trường hợp đồng dạng của tam giác
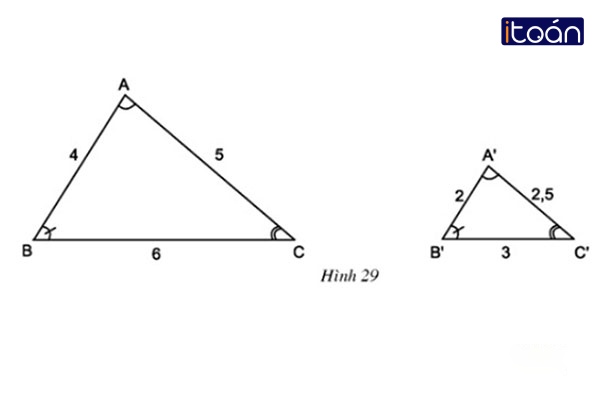
Trường hợp 1: Trường hợp Góc – Góc
Trường hợp đồng dạng thứ nhất của hai tam giác đồng dạng là trường hợp Góc – Góc. Hai tam giác mà có hai cặp góc bằng nhau chính là hai tam giác đồng dạng với nhau.
Khi cho 2 △ABC và △A’B’C’, nếu có góc A = góc A’ và góc B = góc B’ thì △ABC ∼ △A’B’C’.
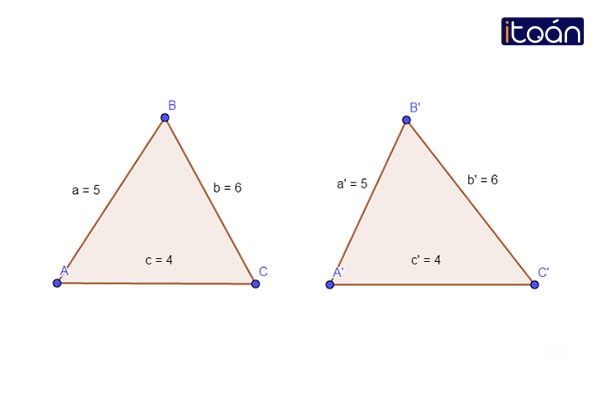
Trường hợp 2: Trường hợp Cạnh – Cạnh – Cạnh
Trường hợp đồng dạng thứ hai của hai tam giác đồng dạng là trường hợp Cạnh – Cạnh – Cạnh. Trường hợp này được phát biểu như sau: Nếu 2 tam giác đã cho trước có 3 cặp cạnh tỉ lệ với nhau thì 2 tam giác đó đồng dạng với nhau.
Khi cho △ABC và △A’B’C’, nếu ![]() thì △ABC ∼ △A’B’C’.
thì △ABC ∼ △A’B’C’.
Trường hợp 3: Trường hợp Cạnh – Góc – Cạnh
Trường hợp đồng dạng thứ ba của hai tam giác đồng dạng là trường hợp Cạnh – Góc – Cạnh. Nếu 2 tam giác đã cho trước có hai cặp cạnh tương ứng tỉ lệ với nhau. Và 2 góc xen giữa bằng nhau. => 2 tam giác này đồng dạng với nhau.
Khi cho △ABC và △A’B’C’, nếu ![]() ‘và góc B = góc B’ thì △ABC ∼ △A’B’C’.
‘và góc B = góc B’ thì △ABC ∼ △A’B’C’.
Trường hợp đồng dạng của 2 tam giác vuông
Ngoài 3 trường hợp đồng dạng trên, các bạn cần phải nắm vững 2 trường hợp khác, bao gồm:
- Trong 2 tam giác vuông, nếu có một cặp góc nhọn bằng nhau thì 2 tam giác đó đồng dạng với nhau.
- Trong 2 tam giác vuông, nếu tồn tại 2 cặp cạnh tỉ lệ tương ứng với nhau thì 2 tam giác đó đồng dạng.
Như vậy, bài viết trên đã cung cấp cho các bạn đọc khái niệm hai tam giác đồng dạng và các tính chất tương ứng. Ngoài ra, việc nắm rõ những trường hợp đồng dạng sẽ giúp các bạn giải bài tập dễ dàng hơn.
>> Xem thêm: Tổng hợp lý thuyết & bài tập: Định lí Ta lét trong tam giác
