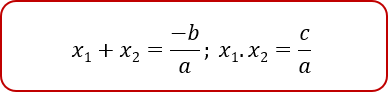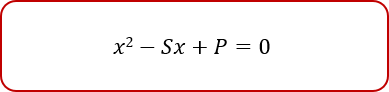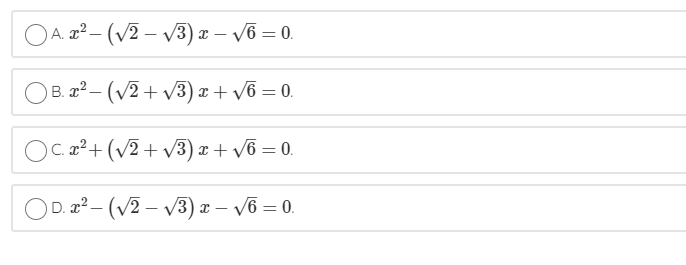Phương trình quy về phương trình bậc nhất, bậc hai – Toán 10

Phương trình quy về phương trình bậc nhất, bậc hai là phần kiến thức trọng điểm của toán 10 đại số. Những đặc điểm, tính chất, lưu ý về phương trình quy về phương trình bậc nhất bậc hai sẽ được Itoan tổng hợp trong bài viết dưới đây. Hãy cùng Itoan khám phá ngay thôi nào!
Kiến thức cần nắm vững
1. Phương trình bậc nhất
Cách giải và biện luận phương trình dạng ax+b=0 được tóm tắt trong bảng sau

2. Phương trình bậc hai
Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau

3. Định lí Vi-ét
Nếu phương trình bậc hai ax2+bx+c=0(a≠0) có hai nghiệm x1,x2 thì:
Ngược lại, nếu hai số u và v có tổng u+v=S và tích u.v=P thì u, v là các nghiệm của phương trình:
Phương trình quy về phương trình bậc nhất, bậc hai
1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối
Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.
Ví dụ:
Giải phương trình: |3x−2|=2x+3 (3)
Giải
Cách 1:
- Nếu 3x−2≥0⇔x≥23 thì (3) ⇔3x−2=2x+3⇔x=5 (thỏa mãn đk x≥23)
⇒x=5 là một nghiệm của phương trình (3).
- Nếu 3x−2<0⇔x<23 thì (1) ⇔−(3x−2)=2x+3⇔5x=−1
⇔x=−15 (thỏa mãn đk x<23)
⇒x=−15 là một nghiệm của phương trình (3).
Vậy phương trình (3) có 2 nghiệm là x1=5;x2=−15.
Cách 2: Bình phương hai vế của phương trình (3) ta được phương trình hệ quả
Phương trình cuối có hai nghiệm là x1=5 và x2=−15.
Thử lại ta thấy 2 nghiệm x1=5; x2=−15 đều thỏa mãn.
Vậy phương trình (3) có 2 nghiệm là x1=5; x2=−15.
2. Phương trình chứa ẩn dưới dấu căn:
Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.
Ví dụ:
Giải phương trình: 2x−3−−−−−√=x−2 (4).
Giải
Điều kiện của phương trình (4) là x≥32.
Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả:
(4) ⇒2x–3=x2–4x+4⇒x2–6x+7=0.
Phương trình cuối có hai nghiệm là x=3+2–√ và x=3–2–√. Cả hai giá trị này đều thỏa mãn điều kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x=3–2–√ bị loại (vế trái dương còn vế phải âm), còn giá trị x=3+2–√ là nghiệm (hai vế cùng bằng 2–√+1).
Vậy nghiệm của phương trình (4) là x=3+2–√.
Bài tập thực hành
Dạng bài cơ bản
Câu 1: Phương trình ax2+bx+c=0 có nghiệm duy nhất khi và chỉ khi:
Câu 2: Tìm điều kiện để phương trình x2+m=0 có nghiệm.
Câu 3: √ và 3–√ là hai nghiệm của phương trình :
Câu 4: Tìm điều kiện để phương trình m(x−m+3)=m(x−2)+6 vô nghiệm.
Câu 5: Cho phương trình x2+2(m+2)x−2m−1=0 (1). Với giá trị nào của thì phương trình (1)có nghiệm?
Câu 6: Với giá trị nào của mx2+2(m−2)x+m−3=0 thì phương trình: có 2 nghiệm phân biệt?
Câu 7: Đáp án nào sau đây sai ?
Câu 8: Tìm điều kiện để phương trình (m2−4m+3)x=m2−3m+2 có nghiệm duy nhất.
Dạng bài nâng cao
Câu 1: Gọi x1, x2 là 2 nghiệm của phương trình 2x2−4x−1=0 . Khi đó, giá trị của T=|x1−x2| bằng bao nhiêu?
Câu 2: Tìm m để phương trình (m2−2)(x+1)=x+2 vô nghiệm.
Câu 3: Tìm điều kiện cho tham số m để phương trình (m−1)x=m−2 có nghiệm âm.
Câu 4: Cho phương trình bậc hai : x2−2(m+6)x+m2=0 . Với giá trị nào của thì phương trình có nghiệm kép và tìm nghiệm kép đó ?
Câu 5: Cho phương trình : m3x=mx+m2−m. Tìm giá trị của tham số m để phương trình có vô số nghiệm.
Trên là những kiến thức và bài tập về Phương trình quy về phương trình bậc nhất, bậc 2.
Xem thêm: