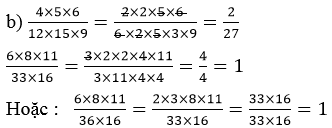Quy đồng mẫu số các phân số – Học tốt toán 4

Những bài học trước chúng ta đã học về các mảng kiến thức của phần phân số . Đây là một phần mới trong chương trình toán lớp 4 , vì vậy cô mong các bạn sẽ cố gắng tập trung lắng nghe các bài giảng để nắm bắt bài thật tốt . Để tiếp nối các bài học trước chúng ta sẽ cùng nhau bước vào bài học hôm nay mang tên : Quy đồng mẫu số các phân số . Bài giảng do Itoan biên soạn dựa trên giáo trình mới nhất của Bộ Giáo dục và Đào tạo . Kính mời các bậc phụ huynh cùng các quý thầy cô tham khảo !
Các bạn đã sẵn sàng học cùng Itoan chưa nào ?
Mục tiêu bài học : Quy đồng mẫu số các phân số
- Sau bài học , các bạn sẽ biết được cách quy đồng mẫu số
- Sử dụng những kiến thức đã học để làm những bài tập từ cơ bản đến nâng cao
Kiến thức cơ bản của bài học : Quy đồng mẫu số các phân số
Sau đây , chúng ta sẽ cùng nhau bước vào học phần lý thuyết cơ bản của bài
I. Quy đồng mẫu số hai phân số
a. Khi quy đồng mẫu số hai phân số có thể làm như sau:
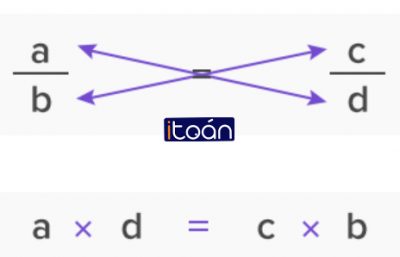
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
b. Nếu mẫu số của phân số thứ hai mà chia hết cho mẫu số của phân số thứ nhất thì ta có thể quy đồng mẫu số hai phân số như sau:
- Lấy mẫu số chung là mẫu số của phân số thứ hai.
- Tìm thừa số phụ bằng cách lấy mẫu số thứ hai cho cho mẫu số thứ nhất.
- Nhân cả tử số và mẫu số của phân số thứ nhất với thừa số phụ tương ứng.
- Giữ nguyên phân số thứ hai
Chú ý: ta thường lấy mẫu số chung là số tự nhiên nhỏ nhất khác 0 và cùng chia hết cho tất cả các mẫu.
II. Ví dụ
Quy đồng mẫu số hai phân số (theo mẫu):
Mẫu :
Ta có :
Vậy quy đồng mẫu số của được
Để hiểu và nắm chắc các kiến thức của bài , chúng ta sẽ cùng nhau lắng nghe bài giảng dưới đây nhé !
Hướng dẫn giải bài tập toán sách giáo khoa bài : Quy đồng mẫu số các phân số
Chúng ta hãy cùng nhau làm một số bài tập dưới đây để củng cố thêm kiến thức nhé !
Bài 1 trang 116 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số:
a)
b)
c)
Phương pháp giải
Khi quy đồng mẫu số hai phân số có thể làm như sau:
– Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
– Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Đáp án:
Các em quy đồng mẫu số như sau:
a)
b)
c)
Giải Toán lớp 4 Bài 2 trang 116 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số:
a)
b)
c)
Phương pháp giải:
Khi quy đồng mẫu số hai phân số có thể làm như sau:
– Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
– Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Đáp án:
Các em quy đồng mẫu số như sau:
a)
b)
c)
Bài 1 trang 116 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số:
a)
b)
c)
Phương pháp giải:
Khi quy đồng mẫu số hai phân số, trong đó mẫu số của một trong hai phân số là mẫu số chung (MSC) ta làm như sau:
– Xác định MSC.
– Tìm thương của MSC và mẫu số của phân số kia.
– Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là MSC.
Đáp án:
Các em quy đồng mẫu số như sau:
a) quy đồng mẫu số thành :
; Giữ nguyên phân số
.
b) quy đồng mẫu số thành:
; Giữ nguyên phân số
.
c) quy đồng mẫu số thành:
; Giữ nguyên phân số
.
Giải Toán lớp 4 Bài 2 trang 117 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số:
a)
b)
c)
d)
e)
g)
Phương pháp giải:
Khi quy đồng mẫu số hai phân số, trong đó mẫu số của một trong hai phân số là mẫu số chung (MSC) ta làm như sau:
– Xác định MSC.
– Tìm thương của MSC và mẫu số của phân số kia.
– Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là MSC.
Đáp án:
Các em quy đồng mẫu số như sau:
a) quy đồng mẫu số thành:
b) quy đồng mẫu số thành:
; Giữ nguyên phân số
.
c) quy đồng mẫu số thành:
; Giữ nguyên phân số
.
d) quy đồng mẫu số thành:
e) quy đồng mẫu số thành:
; Giữ nguyên phân số
g) quy đồng mẫu số thành:
; Giữ nguyên phân số
Giải Toán lớp 4 Bài 3 trang 117 SGK Toán 4 tập 2
Viết các phân số lần lượt bằng các phân số sau và có mẫu số chung là 24:
Phương pháp giải:
Ta có: 24 : 6 = 4 và 24 : 8=3 nên ta viết phân số thành phân số có mẫu số là 24 bằng cách nhân cả tử số và mẫu số với 4; viết phân số
thành phân số có mẫu số là 24 bằng cách nhân cả tử số và mẫu số với 3.
Đáp án:
+) Xét phân số . Vì 24 : 6 = 4 nên ta có:
=
+ Xét phân số . Vì 24 : 8 = 3 nên ta có:
Một số bài tập ôn luyện của bài học : Quy đồng mẫu số các phân số
Bài 1 trang 117 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số:
a) ;
;
;
b) ;
;
.
Phương pháp giải:
Khi quy đồng mẫu số hai phân số có thể làm như sau:
– Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
– Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Đáp án:
a)
Vậy quy đồng mẫu hai phân số được hai phân số
+) Giữ nguyên phân số
Vậy quy đồng mẫu hai phân số được hai phân số
+)
Vậy quy đồng mẫu hai phân số được hai phân số
b) ; giữ nguyên phân số
.
Vậy quy đồng mẫu hai phân số được hai phân số
+) Giữ nguyên phân số .
Vậy quy đồng mẫu hai phân số được hai phân số
+)
Vậy quy đồng mẫu hai phân số được hai phân số
Bài 2 SGK toán 4 trang 117
a) Hãy viết và 2 thành hai phân số đều có mẫu số là 5.
b) Hãy viết 5 và thành hai phân số có mẫu số là 9; là 18.
Đáp án:
a) Viết 2 dưới dạng phân số có mẫu số là 1, sau đó viết phân số đó thành phân số có mẫu số là 5 bằng cách nhân cả tử số và mẫu số với 5; giữ nguyên phân số .
b) +) Viết 5 dưới dạng phân số có mẫu số là 1, sau đó viết phân số đó thành phân số có mẫu số là 9 bằng cách nhân cả tử số và mẫu số với 5; giữ nguyên phân số .
+) Viết 5 dưới dạng phân số có mẫu số là 1, sau đó viết phân số đó thành phân số có mẫu số là 18 bằng cách nhân cả tử số và mẫu số với 18.
Ta có: 18: 9 = 2, do đó ta viết phân số thành phân số có mẫu số là 18 bằng cách nhân cả tử số và mẫu số với 2.
Đáp án
a) Giữ nguyên phân số ;
b); giữ nguyên phân số
.
Giải Toán lớp 4 Bài 3 trang 117 SGK Toán 4 tập 2
Quy đồng mẫu số các phân số sau (theo mẫu):
Mẫu: Quy đồng mẫu số các phân số:
Ta có:
Vậy: Quy đồng mẫu số các phân số:
được .
a)
b)
Phương pháp giải:
Khi quy đồng mẫu số ba phân số có thể làm như sau:
– Lấy tử số và mẫu số của phân số thứ nhất nhân với tích của mẫu số của phân số thứ hai và mẫu số của phân số thứ ba.
– Lấy tử số và mẫu số của phân số thứ hai nhân với tích của mẫu số của phân số thứ nhất và mẫu số của phân số thứ ba.
– Lấy tử số và mẫu số của phân số thứ ba nhân với tích của mẫu số của phân số thứ nhất và mẫu số của phân số thứ hai.
Đáp án:
Vậy quy đồng mẫu số các phân số được
b)
Vậy quy đồng mẫu số các phân số được
Giải Toán lớp 4 Bài 4 trang 118 SGK Toán 4 tập 2
Viết các phân số lần lượt bằng 2 phân số sau và có mẫu số chung là 60:
Phương pháp giải:
Ta có: 60 : 12 = 5 và 60:30 = 2 . Do đó ta viết phân số thành phân số có mẫu số là 60 bằng cách nhân cả tử số và mẫu số với 5; viết phân số
thành phân số có mẫu số là 60 bằng cách nhân cả tử số và mẫu số với 2.
Đáp án
Giải Toán lớp 4 Bài 5 trang 118 SGK Toán 4 tập 2
Tính (theo mẫu):
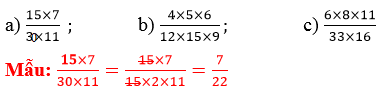
Phương pháp giải:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó lần lượt chia nhẩm tích ở tử số và tích ở mẫu số cho các thừa số chung.
Đáp án: phần b, c
Lời kết
Bài học của chúng ta đã kết thúc , cô mong với bài giảng chi tiết kết hợp với các ví dụ minh họa dễ hiểu sẽ giúp cho các bạn hiểu bài sâu và làm được các bài tập được giao . Itoan cảm ơn các bạn đã đồng hành cùng chúng minh , Itoan sẽ luôn cố gắng , nỗ lực đem đến những bài học hay cho các bạn . Mọi thắc mắc hay muốn xem thêm những bài học thú vị khác , các ban có thể truy cập tại địa chỉ sau : https://learn.toppy.vn/liveclass/
Chúc các bạn học tốt !
Xem thêm :