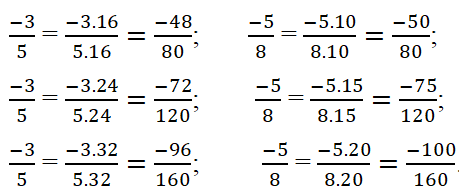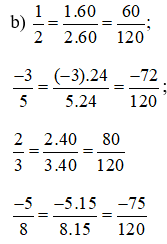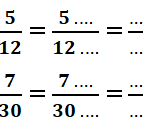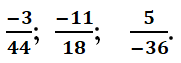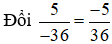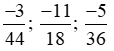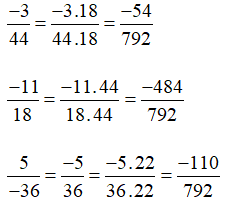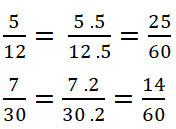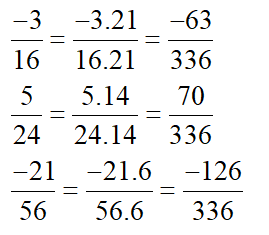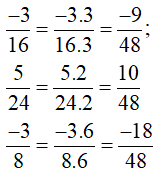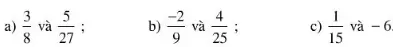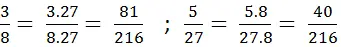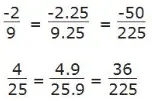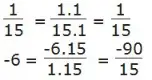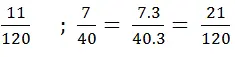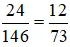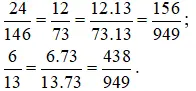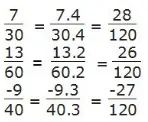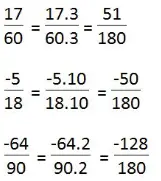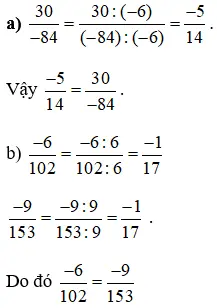Quy đồng mẫu số nhiều phân số – Học tốt toán 6 cùng itoán

Ở bài học trước, chúng ta đã cùng nhau tìm hiểu cách rút gọn phân số như thế nào, sang đến bài học này, các em sẽ được học và tìm hiểu kiến thức về Quy đồng mẫu số nhiều phân số. Nếu như rút gọn phân số ta tìm ước chung lớn nhất rồi chia để tối giản phân số, thì sang đến bài học này, chúng ta sẽ tìm một số bội chung lớn nhất sao cho mẫu của các phân khi quy đồng đều giống nhau. Hãy cùng tìm hiểu sâu hơn qua bài học này nhé!
Mục tiêu bài học
- Hiểu thế nào là quy đồng mẫu hai phân số, nắm được các bước tiến hành quy đồng mẫu hai phân số.
- Có kĩ năng quy đồng mẫu hai phân số (các phân số này có mẫu là các số có không quá 3 chữ số)
Lý thuyết
Vì mọi phân số đều có thể viết dưới dạng phân số có mẫu dương nên ta có quy tắc:
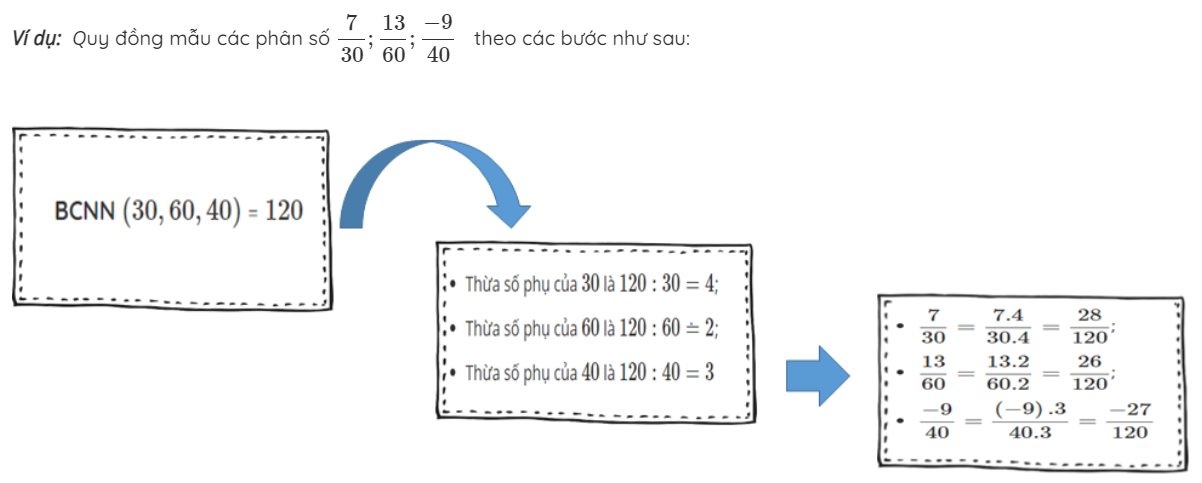
Bước 1: Tìm một bội chung của các mẫu (thường là BCNN) để làm mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng
Giải bài tập Sách giáo khoa Quy đồng mẫu số nhiều phân số
Bài tập SGK rất sát với kiến thức bài giảng, vậy nên chúng ta cùng nhau đi giải các bài tập này nhé!
Toán 6 Tập 2 Bài 5 trang 17: Hãy điền số thích hợp vào ô vuông
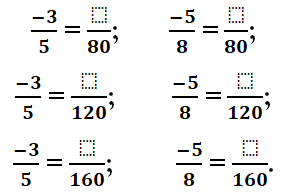
Lời giải
Ta có:
Toán 6 Tập 2 Bài 5 trang 17:
a) Tìm BCNN của các số 2, 5, 3, 8.
b) Tìm các phân số lần lượt bằng 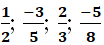
Lời giải
a) Ta có 8 = 23
Các thừa số chung và riêng là 2; 3; 5.
Số mũ lớn nhất của 2 là 3.
Số mũ lớn nhất của 3 là 1.
Số mũ lớn nhất của 5 là 1
Khi đó : BCNN(2,5,3,8) = 23 . 3 . 5 = 120
Toán 6 Tập 2 Bài 5 trang 18:
a) Điền vào chỗ trống để quy đồng mẫu các phân số: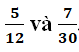
12 = 22 . 3
30 = …
BCNN(12, 30) = …
– Tìm thừa số phụ:
… : 12 = …
… : 30 = …
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
b) Quy đồng mẫu các phân số:
Lời giải
a) – Tìm BCNN( 12,30)
12 = 22.3
30 = 2 . 3 . 5
BCNN(12,30) = 22.3.5 = 60
– Tìm thừa số phụ:
60 : 12 = 5
60 : 30 = 2
b)
⇒ Bài tập đưa về quy đồng mẫu các phân số
– BCNN(44,18, 36)
44 = 22.11
18 = 2.32
36 = 22.32
⇒ BCNN(44,18, 36) = 23.32.11 = 792
– Thừa số phụ
792 : 44 = 18
792 : 18 = 44
792 : 36 = 22
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng;
Bài 28 (trang 19 SGK Toán 6 tập 2):
a) Quy đồng mẫu các phân số sau: −316;524;−2156.
b) Trong các phân số đã cho, phân số nào chưa tối giản ?
Từ nhận xét đó, ta có thể quy đồng các phân số này như thế nào ?
Lời giải
a) Bước 1: Tìm BCNN của 16, 24, 56 để làm MSC
16 = 24
24 = 23.3
56 = 23.7
⇒ BCNN(16, 24, 56) = 24.3.7 = 336
Do đó MSC của ba phân số là 336.
Bước 2: Tìm thừa số phụ của mỗi mẫu.
– Thừa số phụ của 16 là 336 : 16 = 21
– Thừa số phụ của 24 là 336 : 24 = 14
– Thừa số phụ của 56 là 336 : 56 = 6
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
b) Trong các phân số trên thì là phân số chưa tối giản.
Do đó thay vì quy đồng ba phân số 
+ Tìm BCNN(16; 24; 8):
16 = 24; 24 = 23.3; 8 = 23
Suy ra BCNN(16; 24; 8) = 24.3 = 48.
+ Tìm thừa số phụ:
48 : 16 = 3
48 : 24 = 2
48 : 8 = 6.
+ Quy đồng mẫu số:
Bài 29 (trang 19 SGK Toán 6 tập 2): Quy đồng mẫu các phân số sau:
Lời giải
Nhận xét: Các phân số đã cho đều ở dạng tối giản.
a)
Mẫu số chung là BCNN(8, 27) = 8.27 = 216
Thừa số phụ của 8 là 216 : 8 = 27, của 27 là 216 : 27 = 8. Do đó:
b)
Mẫu số chung là BCNN(9, 25) = 9.25 = 225. Do đó:
c) -6 = -6/1
Mẫu số chung là BCNN(15, 1) = 15. Do đó:
Bài 30 (trang 19 SGK Toán 6 tập 2): Quy đồng mẫu các phân số sau:
Lời giải:
a) Các phân số đều tối giản và có mẫu số dương.
Mẫu số chung là BCNN (120, 40) = 120.
Quy đồng mẫu số:
b) Rút gọn
Mẫu số chung là BCNN (73; 13) = 949.
Quy đồng mẫu số
c) Cả ba phân số đều tối giản và mẫu số dương.
Mẫu số chung là BCNN (30,60,40) = 120.
Quy đồng mẫu số:
d) Các phân số đều tối giản.
Mẫu số chung là BCNN(60, 18, 90) = 180.
Quy đồng mẫu số:
Bài 31 (trang 19 SGK Toán 6 tập 2): Hai phân số sau đây có bằng nhau không?
Lời giải:
Ta đưa tất cả các phân số về dạng tối giản rồi so sánh chúng.
Bài tập tự luyện Quy đồng mẫu số nhiều phân số
Câu 1: Mẫu số chung của các phân số là:
A. 240
B. 16
C. 20
D. 38
Câu 2: Quy đồng mẫu số các phân số được các phân số lần lượt là:
A. B.
C. D.
Câu 3: Mẫu chung nguyên dương nhỏ nhất của hai phân số là:
A.
B.
C.
D.
Câu 4: Quy đồng mẫu số hai phân số được hai phân số lần lượt là
A.
B.
C.
D.
Câu 5: Tìm mẫu số chung nhỏ nhất của
a, Hai phân số và
b, Hai phân số và
Đáp án tự luyện
Câu 1: C
Câu 2: C
Câu 3: B
Câu 4: D
Câu 5:
a, Mẫu số chung nhỏ nhất của hai phân số bằng BCNN của hai mẫu
Vậy mẫu số chung nhỏ nhất của hai phân số hai BCNN() là
b, Mẫu số chung nhỏ nhất của hai phân số bằng BCNN của hai mẫu
Vậy mẫu số chung nhỏ nhất của hai phân số hai BCNN() là
Kết luận
Quy đồng mẫu số của nhiều phân số là biến đổi những phân số đó lần lượt thành những phân số bằng chúng nhưng có cùng mẫu số. Qua bài học này, các em đã hiểu thế nào là quy đồng mẫu số và cách để quy đồng mẫu số. Ngoài ra, ở Toppy còn cung cấp khá nhiều bài học bổ ích khác nữa, các em có thể đăng nhập vào trang web làm bài luyện tập, củng cố và nâng cao bài học hôm nay.
Mở rộng
Ở phần Đại số lớp 6, các em sẽ được phát triển và nâng cao kiến thức về phân số đã học ở bậc Tiểu học. Để các em nắm vững được kiến thức học kỳ II, chúng ta sẽ phân ra các nhóm kiến thức sau đây:
– Nhóm kiến thức cơ bản:
- Khái niệm & tính chất phân số;
- Rút gọn phân số;
- Quy đồng mẫu số
– Nhóm kiến thức tính toán:
- So sánh phân số;
- Các phép toán phân số;
- Hỗn số, số thập phân, phần trăm
– Nhóm kiến thức vận dụng:
- Quy tắc tìm giá trị phân số của một số cho trước;
- Quy tắc tìm một số biết giá trị một phân số của nó;
- Cách tính tỷ số a và b? Tỷ số phần trăm?
- Vận dụng bài toán thực tế
Nhìn chung, kiến thức của học kỳ II là phần tiếp nối và mở rộng của học kỳ I. Để đạt được kết quả tốt trong kỳ thi cũng như nắm chắc được nội dung các bài học, các em cần thiết lập mục tiêu và ôn tập kiến thức trọng tâm qua các nhóm kiến thức cô đã tổng hợp phía trên. Chúc các em học tập tốt!