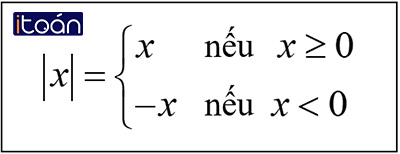Giá trị tuyệt đối của số hữu tỉ- Cộng, trừ, nhân, chia số thập phân – Toán lớp 7

Bài giảng: Giá trị tuyệt đối của số hữu tỉ – Cộng, trừ, nhân, chia số thập phân – Bài tập & Lời giải SGK Toán lớp 7, được các thầy cô giáo chuyên môn cao của iToan biên soạn. Vẫn là những kiến thức cũ theo chương trình sách giáo khoa, nhưng được giảng dạy theo phương pháp mới, trực quan hơn, thú vị hơn, giúp mỗi giờ học Toán của học sinh không còn khó khăn hay nhàm chán. Bài giảng bao gồm: lý thuyết cơ bản cần nắm, hướng dẫn giải bài tập sách giáo khoa & Các bài tập tự luyện giúp em tiến bộ.

Các em cùng tham khảo nhé!

Lý thuyết Giá trị tuyệt đối của số hữu tỉ – Cộng, trừ, nhân, chia số thập phân

Giá trị tuyệt đối của một số hữu tỉ

Giá trị tuyệt đối của số hữu tĩ x, ký hiệu |x\, là khoảng cách từ điểm x tới điểm 0 trên trục số.

Ta có:

Nhận xét: Với mọi x∈Q ta luôn có: |x|≥0, |x|=|−x| và |x|≥x

Cộng, trừ, nhân, chia số thập phân

Để cộng, trừ, nhân, chia các số thập phân, ta có thể viết chúng dưới dạng phân số thập phân rồi làm theo quy tắc các phép tính đã biết về phân số.

Trong thực hành, ta thường cộng, trừ, nhân hai số thập phân theo các quy tắc về giá trị tuyệt đối và về dấu tương tự như đối với số nguyên.

Khi chia số thập phân x cho số thập phân y (y≠0), ta áp dụng quy tắc: Thương của hai số thập phân x và y là thương của |x| và |y| với dấu “+” đằng trước nếu x và y cùng dấu và dấu “−”đằng trước nếu x và y khác dấu.

Ví dụ

Ví dụ 1: Tìm |x|, biết:

a. x=−1/7;

b. x=0

Giải:

a. Với  x=−1/7 thì |x| = ∣−1/7∣=1/7

b. Với x=0 thì |x| = |0| = 0

Ví dụ 2: Tính:

a. (−3,116)+0,263;

b. (−3,7).(−2,16).

Giải:

a. (−3,116)+0,263=−2,853.

b. (−3,7).(−2,16)=3,7.2,16=7,992.

Giải bài tập SGK Toán 7 trang 31 Giá trị tuyệt đối của số hữu tỉ – Cộng, trừ, nhân, chia số thập phân

Bài 31: Tìm x ∈ Q, biết:

a)  |2,5 – x| = 1,3

b)  1,6 – | x – 0,2 | = 0

c)  |x – 1,5 | + |2,5 – x | = 0

Lời giải: 

a) Ta có 2,5 – x = 1,3 hoặc 2,5 – x = -1,3.

Từ đó,  tìm được   x = 1,2 hoặc x = 3,8.

b) Ta có x – 0,2 = 1,6 hoặc  x – 0,2 = -1,6.

Từ đó : x = 1,8 hoặc x = -1,4.

c) Vì | x- 1,5 | >0    ;     |2,5 – x |> 0 do đó phải có :

x – 1,5 = 2,5 – x = 0 suy ra x = 1,5 và Xx = 2,5. Điều này không thể đồng thời xảy ra. Vậy không tồn tại x thoả mãn yêu cầu của đề bài.

Bài 32. Tìm giá trị lớn nhất của:

A = 0,5 – | x – 3,5 |

B = – | 1,4 – x | – 2

Lời giải: 

A = 0,5 – | x – 3,5 | < 0,5.

A đạt giá trị lớn nhất là 0,5 khi    x = 3,5.

B = – |1,4 – x | – 2  ≤ -2.

B đạt giá trị lớn nhất là -2 khi x =   1,4.

Bài 33. Tìm giá trị nhỏ nhất của:

C = 1,7 + | 3,4 – x|

D = | 1,4 – x | – 2

Lời giải:

C = 1,7 + | 3,4 – x | > 1,7

C đạt giá trị nhỏ nhất là 1,7 khi x = 3,4.

D = | x + 2,8 | -3,5  ≥  -3,5.

D đạt giá trị nhỏ nhất là -3,5 khi x = -2,8.

Bài 34. Đặt một cặp dấu ngoặc () vào biểu thức ở vế trái để được kết quả đúng bằng vế phải:

a) 2,2 – 3,3 + 4,4 – 5,5 + 6,6 = -8,8 ;

b) 2,2 – 3,3 + 4,4 – 5,5 + 6,6 = -4,4 ;

c) 2,2 – 3,3 + 4,4 – 5,5 + 6,6 = 6,6 ;

d) 2,2 – 3,3 + 4,4 – 5,5 + 6,6 = -6,6.

Lời giải:

a) 2,2 – 3,3 + 4,4 – (5,5 + 6,6) = -8,8.

b) 2,2 – (3,3 + 4,4) – 5,5 + 6,6 = – 4,4.

c) 2,2 – (3,3 + 4,4 – 5,5) + 6,6 = 6,6.

d) 2,2 – (3,3 + 4,4 – 5,5 + 6,6) = – 6,6.

Bài 35. Tính :

12345,4321 . 2468,91011 + 12345,4321 . (-2468,91011).

Lời giải: 

12345,4321 . [2468,91011 + (-2468,91011)] = 0.

Bài 36. Đúng hay sai ?

5,7 . (7,865 . 31,41) = (5,7 . 7,865). (5,7 . 31,41).

Lời giải:

Sai, không có tính chất phân phối của phép nhân đối với phép nhân.

Bài 37. Giả sử x ∈ Q. Kí hiệu [x], đọc là phần nguyên của x, là số nguyên lớn nhất không vượt quá x, nghĩa là [x] là số nguyên sao cho [x] < x < [x] + 1.

Tìm [ 2, 3] , [  ]  ,  [-4]  ,  [-5,16]

Lời giải:

2 < 2,3 < 3 => [2,3] = 2

o <     < 1   => [   ] = 0

4 < -4 < -3 => [-4] = – 4

6 < -5,16 < -5 => [-5,16] = – 6.

Bài 38.

Giả sử x ∈ Q.  Kí hiệu {x} đọc là phần lẻ của X, là hiệu x – [x], nghĩa là : { x } = x — [x].

Tìm {x}, biết : x = 0,5              ;              x = -3,15.

Lời giải:

x = 0,5 => [x] = 0. Do đó {x} = 0,5 – o = 0,5.

x = -3,15 => [x] = -4. Do đó {x} = -3,15 – (- 4) = 0,85.

Bài tập tự luyện Giá trị tuyệt đối của số hữu tỉ – Cộng, trừ, nhân, chia số thập phân

Các bài tập tự luyện sẽ giúp các em làm thành thạo và chính xác hơn các dạng toán tương tự!

Phần câu hỏi

Câu 1: Câu nào sau đây là sai:

A. |10,5|=10,5

B. |−10,5|=10,5

C. |10,5|=−10,5

D. |−10,5|=−(−10,5)

Câu 2: Chọn câu đúng. Nếu x≥0 thì:

A. |x|=x

B. |x|=−x

C. |x|<0

D. |x|=0

Câu 3: Ta tìm được bao nhiêu số x>0 thỏa mãn |x|=2 ?

A. 0

B. 1

C. 2

D. 3

Câu 4: Tìm tất cả các giá trị của x thỏa mãn: |x| = |−9/5|

A. x=0

B. x=9/5

C. x=−9/5

D. x=±9/5

Câu 5: Tính nhanh: 21,6+34,7+78,4+65,3 ta được kết quả là:

A. 50

B. 100

C. 200

D. 300

Phần đáp án

1.C       2.A       3.B       4.D       5.C

Lời kết

Gía trị tuyệt đối của số hữu tỉ là một khái niệm hoàn toàn mới, nhưng sẽ không có gì khó khăn nếu các em nhớ được quy tắc, tính chất của nó. Để học tốt môn Toán cũng như các môn học khác trong chương trình lớp 7, hãy học cùng Toppy. Toppy có đội ngũ thầy cô giáo trực tuyến cùng nguồn tài liệu chất lượng được biên soạn kĩ càng, chắc chắn sẽ giúp các em tiến bộ và chinh phục kiến thức dễ dàng.

>> Xem thêm các bài giảng khác tại iToan:

• Tìm số chia- bài tập & Lời giải SGK
• Phép trừ dạng 33 – 5
• Phép trừ dạng 53 – 15
• Phép trừ dạng 55 – 8, 56 – 7, 68 – 9