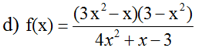Dấu của tam thức bậc 2 – Tổng hợp lý thuyết đáng chú ý

Dấu của tam thức bậc 2 là một chuyên đề các em đã được làm quen trước đây. Tuy nhiên, với đại số lớp 10, một lần nữa các em sẽ được gặp lại khái niệm này. Với lượng kiến thức lớn và chuyên sâu hơn. Đồng thời, các dạng bài tập cũng được mở rộng và nâng lên ở mức khó. Vì thế, hãy cùng Itoan tập trung học và cùng nhau luyện tập thêm về chuyên đề này nhé!
Dấu của tam thức bậc 2 – Tổng hợp lý thuyết đáng chú ý
Định nghĩa
Tam thức bậc hai là những biểu thức chứa ẩn x, có dạng:
f(x) = ax2 + bx + c,
trong đó, ta có a, b, c là những hệ số, thỏa mãn điều kiện a ≠ 0. Và x là ẩn

Dấu của tam thức bậc 2
Định lý
Cho f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac.
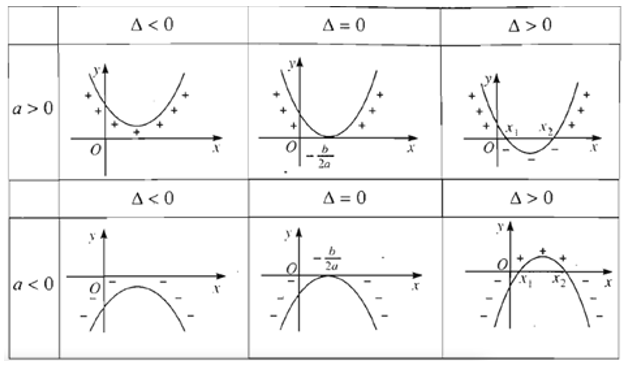
Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R.
Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi x = –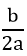
Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x1 hoặc x > x2, trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 (x1 < x2) là hai nghiệm của f(x).
Chú ý
Trong định lí trên, có thể thay biệt thức Δ = b2 – 4ac bằng biệt thức thu gọn Δ’ = (b’)2 – ac
Minh họa hình học
Định lí về dấu của tam thức bậc hai có minh họa hình học sau
Bài tập thực hành tam thức bậc hai
Bài 1 (trang 105 SGK Đại Số 10):
Xét dấu các tam thức bậc hai:
a) 5x2 – 3x + 1 ; b) -2x2 + 3x + 5
c) x2 + 12x + 36 ; d) (2x – 3)(x + 5)
Lời giải
a) Tam thức f(x) = 5x2 – 3x + 1 có Δ = 9 – 20 = –11 < 0 nên f(x) cùng dấu với hệ số a.
Mà a = 5 > 0
Do đó f(x) > 0 với ∀ x ∈ R.
b) Tam thức f(x) = –2x2 + 3x + 5 có Δ = 9 + 40 = 49 > 0.
Tam thức có hai nghiệm phân biệt x1 = –1; x2 = 5/2, hệ số a = –2 < 0
Ta có bảng xét dấu:

f(x) = 0 khi x = –1 ; x = 5/2
f(x) < 0 khi x ∈ (–∞; –1) ∪ (5/2; +∞)
c) Tam thức f(x) = x2 + 12x + 36 có một nghiệm là x = –6, hệ số a = 1 > 0.
Ta có bảng xét dấu:

f(x) = 0 khi x = –6
d) f(x) = (2x – 3)(x + 5) = 2x2 + 7x – 15
Tam thức f(x) = 2x2 + 7x – 15 có hai nghiệm phân biệt x1 = 3/2; x2 = –5, hệ số a = 2 > 0.
Ta có bảng xét dấu:

f(x) = 0 khi x = –5 ; x = 3/2
f(x) < 0 khi x ∈ (–5; 3/2)
Bài 2 (trang 105 SGK Đại Số 10):
Lập bảng xét dấu các biểu thức sau:
a) f(x) = (3x2 – 10x + 3)(4x – 5)
b) f(x) = (3x2 – 4x)(2x2 – x – 1)
c) f(x) = (4x2 – 1)(-8x2 + x – 3)(2x + 9)
Lời giải
a) f(x) = (3x2 – 10x + 3)(4x – 5)
+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.+ Nhị thức 4x – 5 có nghiệm x = 5/4.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
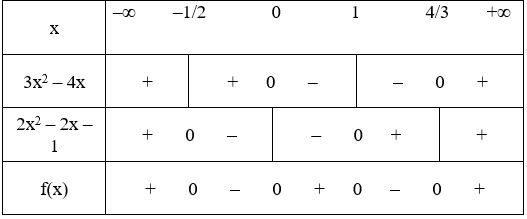
b) f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
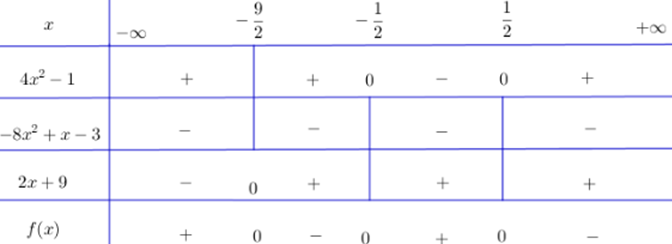
c) f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
+ Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0
Do đó 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2
+ Tam thức –8x2 + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên luôn mang dấu –.
+ Nhị thức 2x + 9 có nghiệm x = –9/2.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
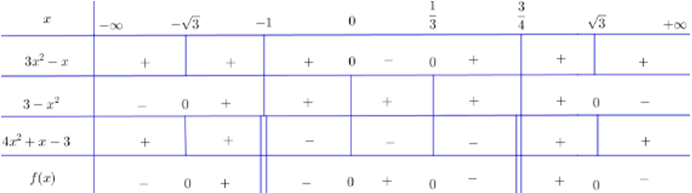
+ Tam thức 3x2 – x có hai nghiệm x = 0 và x = 1/3, hệ số a = 3 > 0.
Do đó 3x2 – x mang dấu + khi x < 0 hoặc x > 1/3 và mang dấu – khi 0 < x < 1/3.
+ Tam thức 3 – x2 có hai nghiệm x = √3 và x = –√3, hệ số a = –1 < 0
Do đó 3 – x2 mang dấu – khi x < –√3 hoặc x > √3 và mang dấu + khi –√3 < x < √3.
+ Tam thức 4x2 + x – 3 có hai nghiệm x = –1 và x = 3/4, hệ số a = 4 > 0.
Do đó 4x2 + x – 3 mang dấu + khi x < –1 hoặc x > 3/4 và mang dấu – khi –1 < x < 3/4.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–√3; –1) ∪ (0; 1/3) ∪ (3/4; √3)
f(x) = 0 ⇔ x ∈ {±√3; 0; 1/3}
f(x) < 0 ⇔ x ∈ (–∞; –√3) ∪ (–1; 0) ∪ (1/3; 3/4) ∪ (√3; +∞)
f(x) không xác định khi x = -1 và x = 3/4.
Lời kết
Trên đây là bài viết nội dung về chủ đề Tam thức bậc 2. Hy vọng đây sẽ là những kiến thức bổ ích dành cho các bạn học sinh. Đặc biệt là quý phụ huynh có nhu cầu ôn tập và giảng dạy cho các em. Trong quá trình học tập và ôn luyện, nếu có nhu cầu tìm kiếm đơn vị học tập uy tín, chất lượng. Hoặc muốn được giải đáp về những kiến thức liên quan đến môn học, hãy liên hệ với Itoan để được giải đáp nhanh nhất có thể