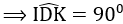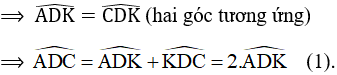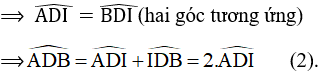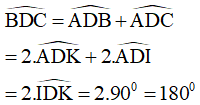Tính chất ba đường trung trực của tam giác – SGK Toán lớp 7

Ở bài hôm trước chúng ta đã được học về tính chất của đường trung trưc của đoạn thẳng. Trong bài hôm nay, các thầy cô iToan sẽ dạy các em bài: Tính chất ba đường trung trực của tam giác– Bài tập & Lời giải SGK Toán 7 với phương pháp giảng dạy trực quan, ví dụ minh họa, hình vẽ dễ hiểu. Cùng tập trung vào bài học nhé!
Lý thuyết: Tính chất ba đường trung trực của tam giác
Đường trung trực
-
-
-
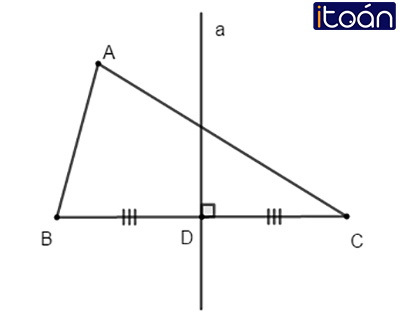
- Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.
-
-
Ví dụ: Trên hình vẽ a là đường trung trực ứng với cạnh BC của tam giác ΔABC.
-
-
-
- Mỗi tam giác có ba đường trung trực.
-
-
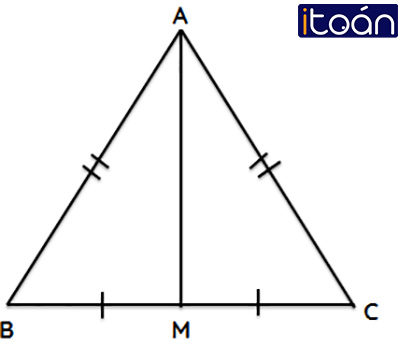
Tính chất: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.
Tính chất ba đường trung trực của tam giác
Ba đường trung trực của cùng một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
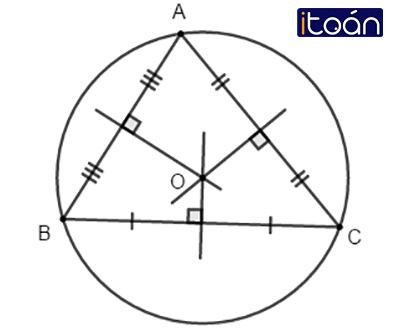
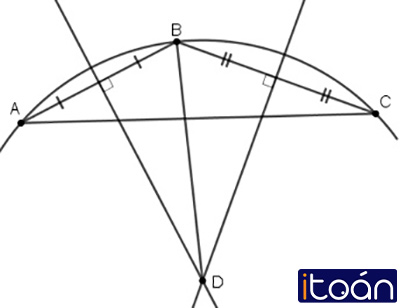
Ví dụ: Điểm O là giao điểm ba đường trung trực của tam giác ΔABC, ta có OA=OB=OC.
Chú ý: Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A,B,C. Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC.
Cùng xem thêm video bài giảng của cô giáo để hiểu bài kĩ và nhớ lâu hơn các em nhé!
Giải bài tập SGK Toán 7 trang 79 Tính chất ba đường trung trực của tam giác
Bài 52
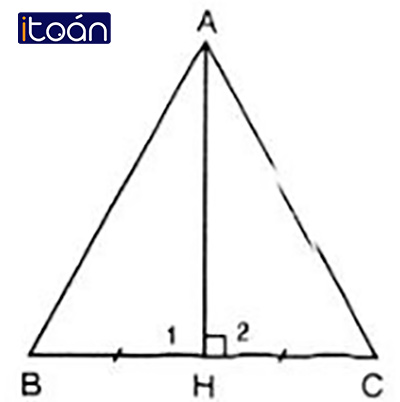
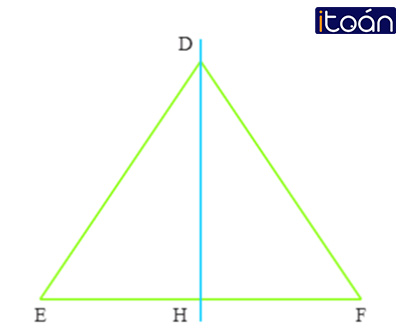
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.
Lời giải:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
Bài 53
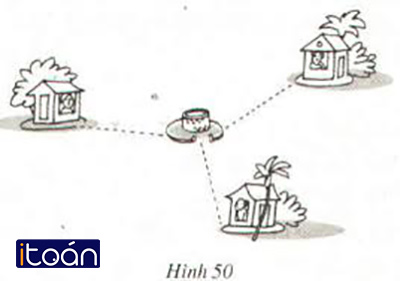
Ba gia đình quyết định đào chung một cái giếng (h.50). Phải chọn vị trí của giếng ở đâu để các khoảng cách từ giếng đến các nhà bằng nhau?
Lời giải:
Gọi vị trí ba ngôi nhà lần lượt là A, B, C, vị trí giếng cần đào là O.
Vì điểm O cách đều ba điểm A, B, C nên O là giao của ba đường trung trực của AB, BC, CA (hay O là tâm đường tròn ngoại tiếp tam giác ABC).
Tuy nhiên để xác định O ta chỉ cần xác định hai trong ba đường trung trực rồi cho chúng cắt nhau vì ba đường trung trực đều đồng quy tại một điểm.
Bài 54
Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:
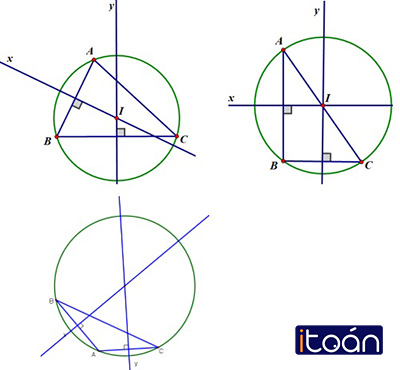
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó.
Để vẽ đường tròn ta cần:
+ Vẽ đường trung trực y của cạnh BC.
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm I bán kính IA.
Nhận xét:
– Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
– Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền (chứng minh bài 56).
Bài 55
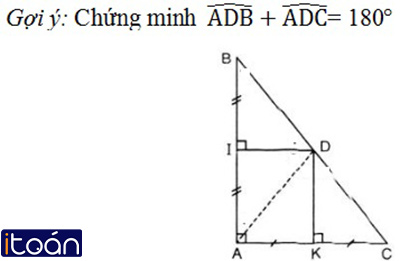
Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.
Từ hình vẽ ta có:
+ DK là đường trung trực của AC ⇒ DA = DC.
+ DI là đường trung trực của AB ⇒ DA = DB.
+ Ta có : DI // AC (vì cùng ⏊ AB)
Mà DK ⏊ AC ⇒ DK ⏊ DI
+ Xét ∆ADK và ∆CDK có:
AD = DC
AK = CK (gt)
DK chung
⇒ ∆ADK = ∆CDK (c.c.c)
+ Xét ∆ADI và ∆BDI có :
AD = BD
AI = BI (gt)
DI chung
⇒ ∆ADI = ∆BDI (c.c.c)
Từ (1) và (2) suy ra
Vậy B, D, C thẳng hàng.
Bài 56
Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
Lời giải:
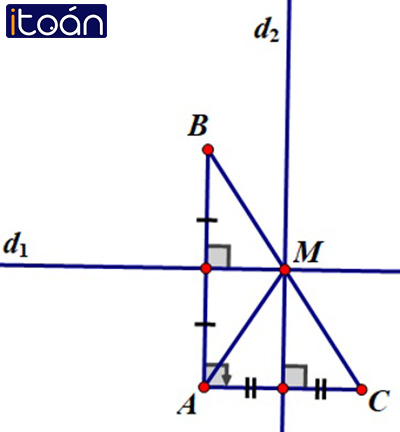
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Bài 57
Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy. Làm thế nào để xác định được bán kính của đường viền này?
Lời giải:
– Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
– Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.
Bài tập tự luyện Tính chất ba đường trung trực của tam giác
Phần câu hỏi
Câu 1: Chọn phát biểu đúng:
A. Trong một tam giác cân, đường trung trực của cạnh bên đồng thời là đường cao của tam giác ứng với cạnh đó.
B. Trong một tam giác cân, tâm đường tròn ngoại tiếp tam giác luôn nằm trong tam giác đó.
C. Trong một tam giác đều, đường trung trực đồng thời cũng là đường cao của tam giác.
D. Trong một tam giác vuông, tâm đường tròn ngoại tiếp tam giác luôn nằm ngoài tam giác đó.
Câu 2: Nếu tam giác ABC là tam giác tù thì:
A. Tâm đường tròn ngoại tiếp tam giác luôn nằm bên ngoài tam giác.
B. Tâm đường tròn ngoại tiếp tam giác luôn nằm bên trong tam giác.
C. Tâm đường tròn ngoại tiếp tam giác nằm trên 1 cạnh của tam giác.
D. Tâm đường tròn ngoại tiếp tam giác cách đều ba cạnh của tam giác.
Câu 3: Biết rằng DH là trung trực của đoạn EF. Độ dài DE=23cm.DF=...cm?
A. 23
B. 20
C. 11,5
D. 25
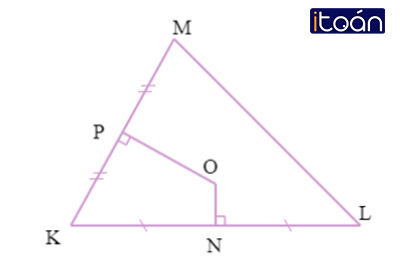
Câu 4: Cho hình vẽ, biết rằng O là giao điểm của trung trực cạnh KL và KM. Nối O,OL,OM, độ dài đoạn OL=32cm.
OM=...cm?
A. 16
B. 30
C. 32
D. 48
Câu 5: Cho tam giác ABC vuông tại A. Gọi M,N lần lượt là trung điểm của AB,AC. Gọi O là giao điểm của 2 đường trung trực của các cạnh AB,AC. Phát biểu nào không đúng:
A. Tứ giác AMON là hình vuông
B. Ba điểm O,C,B thẳng hàng
C. ΔAOM=ΔBOM
D. ΔAON=ΔCON
Phần đáp án
- C 2. A 3. A 4.C 5.A
Lời kết
Bài học Tính chất ba đường trung trực của tam giác đến đây là kết thúc. Toán lớp 7 có nhiều dạng toán mới lạ và khó, để giải quyết các khó khăn trong học tập cũng như ôn tập trước mỗi kì thi, hãy cùng học với Toppy.
Chúc các em luôn học tốt và đạt nhiều thành tích cao trong học tập!
>> Xem thêm: