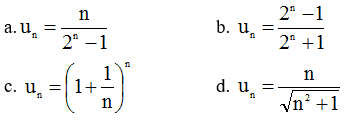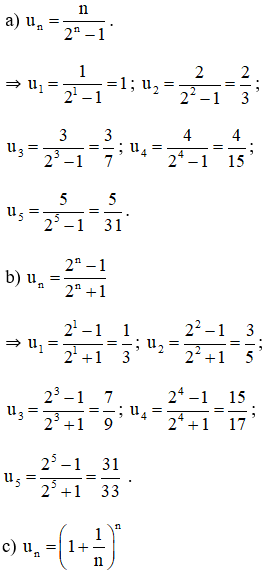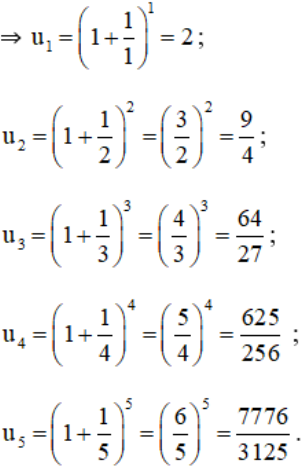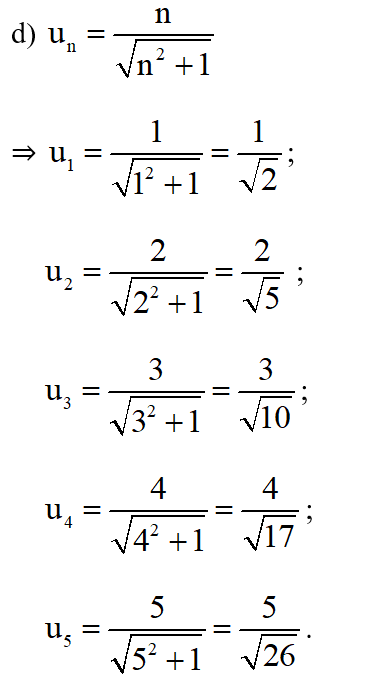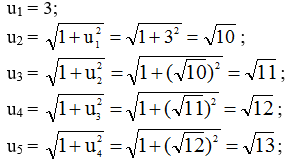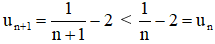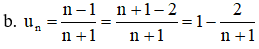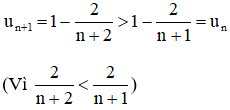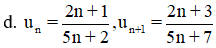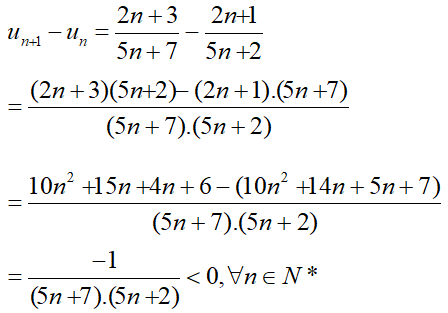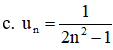Bài tập về dãy số- Đại số 11

Các em đã được làm quen với dãy số từ tiểu học và học xuyên suốt những năm cấp 2, cấp 3. Trong chương trình toán 11, các em sẽ tiếp tục học về hàm số, nhưng sẽ nâng cao và tổng quát hơn. Bài giảng: Dãy số– Đại số 11 do iToan biên soạn với mục tiêu giúp các em tổng hợp lại kiến thức lý thuyết và hướng dẫn giải các bài tập SGK & Bài luyện tập chuyên đề dãy số.
Bài giảng gồm 3 phần chính
- Tổng hợp lý thuyết cần nắm
- Hướng dẫn giải bài tập SGK Đại số 11 trang
- Bài tập tự luyện
Lý thuyết cần nắm bài Dãy số
Định nghĩa dãy số
a. Định nghĩa dãy số
Một hàm số xác định trên tập hợp các số nguyên dương được gọi là một dãy số vô hạn (hay gọi tắt là là dãy số). Kí hiệu:
Mỗi giá trị của hàm số u được gọi là một số hạng của dãy số, u(1) được gọi là số hạng thứ nhất (hay số hạng đầu), u(2) được gọi là số hạng thứ hai…
Người ta thường kí hiệu các giá trị u(1),u(2),... tương ứng bởi u1,u2,... và thường kí hiệu dãy số u=u(n) bởi (un) và gọi un là số hạng tổng quát của dãy số đó.
Dãy số (un) thường được viết dưới dạng khai triển: u1,u2,...,un,...,
Ví dụ: Dãy các số tự nhiên lẻ 1,3,5,7,…, có số hạng đầu là u1=1 , số hạng tổng quát un=2n−1
b. Dãy số hữu hạn
- Mỗi hàm số u xác định trên tập M={1,2,3,...,m} với được gọi là một dãy số hữu hạn.
- Dạng khai triển của nó là , trong đó là số hạng đầu, là số hạng cuối.
Ví dụ: −5,−2,1,4,7,10,13 là dãy số hữu hạn có u1=−5,u7=13
Cách cho một dãy số
a. Dãy số cho bằng công thức của số hạng tổng quát
Ví dụ: Cho dãy un với un=2n2−3n+2 (1)
Từ công thức (1) ta có thể xác định được bất kì số hạng nào của dãy các số. Chẳng hạn,
u3=2.32−3.3+2=11
Nếu viết dãy sau dưới dạng khai triển ta được
1,4,11,22,…,2n2−3n+2
b. Dãy số cho bằng công thức mô tả
Ví dụ: Số π là số thập phân vô hạn không tuần hoàn
π=3,141592653589…
Nếu lập dãy (un) với un là giá trị gần đúng thiếu của số π với sai số tuyệt đối thì
u1=3,1;u2=3,14;u3=3,141;u4=3,1414;…
Đó là dãy các số cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.
c. Dãy số cho bằng phương pháp truy hồi
Cho một dãy các số bằng phương pháp truy hồi tức là:
- Cho số hạng đầu (hay vài số hạng đầu).
- Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
Giải bài tập SGK Dãy số
Bài 1 (trang 92 SGK Đại số 11):
Viết năm số hạng đầu của dãy có số hạng tổng quát un cho bởi công thức:
Lời giải:
Bài 2 (trang 92 SGK Đại số 11):
Cho dãy (un), biết u1 = – 1, un+ 1 = un + 3 với n ≥ 1
a. Viết năm số hạng đầu của dãy trên;
b. Chứng minh bằng phương pháp quy nạp: un = 3n – 4
Lời giải:
a. u1 = – 1, un + 1 = un + 3 với n > 1
u1 = – 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 – 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) – 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.
Bài 3 (trang 92 SGK Đại số 11):
Dãy các số (un) cho bởi u1 = 3, un+1 = √(1+un2) , n > 1
a. Viết năm số hạng đầu của dãy.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
Lời giải:
a. Năm số hạng đầu của dãy sau:
b. Dự đoán công thức số hạng tổng quát của dãy sau:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*
Bài 4 (trang 92 SGK Đại số 11):
Xét tính tăng, giảm của các dãy (un), biết:
Lời giải:
a. Với mọi n ∈ N ta có:
⇒ (un) là dãy các số giảm.
Với mọi n ∈ N có:
⇒ (un) là dãy các số tăng.
c. un = (-1)n.(2n + 1)
Nhận xét: u1 < 0, u2 > 0, u3 < 0, u4 > 0, …
⇒ u1 < u2, u2 > u3, u3 < u4, …
⇒ dãy số (un) không tăng, không giảm
với n ∈ N*, n ≥ 1
Xét:
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm
Bài 5 (trang 92 SGK Đại số 11):
Trong các dãy (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn?
Lời giải:
a. un = 2n2 – 1
+ Với n ∈ N* ta có: n ≥ 1 và n2 ≥ 1
⇒ un = 2n2 – 1 ≥ 2.12 – 1 = 1.
⇒ un ≥ 1
⇒ dãy (un) bị chặn dưới ∀n ∈ N*.
+ (un) không bị chặn trên vì không có số M nào thỏa mãn:
un = 2n2 – 1 ≤ M ∀n ∈N*.
Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn.
b. Ta có : 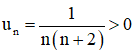
⇒ (un) bị chặn dưới
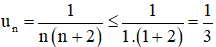
⇒ (un) bị chặn trên.
Vậy (un) là dãy bị chặn.
+ Ta có : 2n2 – 1 > 0 ∀ n ∈ N*
⇒ 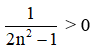
⇒ (un) bị chặn dưới.
+ 2n2 – 1 ≥ 2.1 – 1 = 1
⇒ 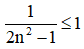
d. un = sin n + cos n.
Vậy dãy số (un) bị chặn.
Bài tập tự luyện Dãy số
Các bài tập tự luyện của iToan sẽ giúp các em rèn luyện tư duy logic, giải nhanh các bài toán trắc nghiệm!
Phần câu hỏi
Câu 1: Cho dãy có 4 số hạng đầu là:−1;3;19;53 . Hãy tìm một quy luật của dãy trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.
A. u10=97
B. u10=71
C. u10=1414
D. u10=971
Câu 2: Cho dãy các số có các số hạng đầu là:8,15,22,29,36,... .Số hạng tổng quát của dãy các số này là:
A. un=7n+7
B. un=7n
C. un=7n+1
D. un: Không viết được dưới dạng công thức.
Câu 3:
Câu 4:
Câu 5:

Phần đáp án
1.A 2.C 3.A 4.B 5.A
Lời kết
Dạng toán trên được ứng dụng rất nhiều trong đề thi THPT Quốc gia. Để ôn tập thêm về dạng toán này cũng như nhiều dạng khác, các em haxcos thể học trực tuyến với nền tảng Toppy. Toppy có đầy đủ các bài giảng basom sát theo chương trình SGK, giúp các em củng cố và nâng cao kiến thức.
Cùng Toppy học tốt nhé!
>> Xem thêm: